CopyRight 2009-2020 © All Rights Reserved.版权所有: 中国海关未经授权禁止复制或建立镜像
标准曲线法在再生纤维素纤维溶解法定量分析中的应用研究
作者:赵素敏 高友军 刘锦瑞 窦彩云 张向丽1
赵素敏 高友军 刘锦瑞 窦彩云 张向丽1
再生纤维素纤维混纺产品(如莱赛尔A100与竹纤维、莱赛尔A100与粘胶等)中纤维成分定量分析方法——溶解法已被本实验室研究建立,其中在数据处理时采用标准曲线法代替传统的给定损伤系数d值法,开创了再生纤维素纤维定量分析方法的先河。本文重点对再生纤维素纤维定量分析方法——溶解法在进行数据处理应用标准曲线法时容易出现的问题和解决办法进行深入研究和阐述。
关键词 再生纤维素纤维;溶解法;纤维成分;标准曲线法;数据处理
Application Research of Standard Curve Method in Quantitative Analysis of Regenerated Cellulose Fibers by Dissolution Method
ZHAO Su-Min1GAO You-Jun1LIU Jin-Rui1DOU Cai-Yun1ZHANG Xiang-Li1
Abstract The dissolution method for quantitative analysis of fiber components of regenerated cellulose fiber blended products (such as Lyocell A100 and bamboo fiber, Lyocell A100 and viscose, etc.) has been established in our laboratory, in which the standard curve method has been used to replace the traditional d-value method of given damage coefficient in the data processing. The method has opened up a precedent for quantitative analysis of regenerated cellulose fibers. This paper focuses on deeply studying and elaborating in the problems and solutions, which are easy to occur when applying the standard curve method for data processing of the quantitative analysis method of regenerated cellulose fiber using the dissolution method.
Keywords Regenerated cellulose fiber; dissolution method;fiber component; standard curve method; data processing
引言
目前,对于再生纤维素纤维的研究大多集中在棉或其他纤维与再生纤维素纤维的分析,较少有再生纤维素纤维之间的研究,特别是采用溶解法分析再生纤维素纤维的混纺产品成分的文献,除本实验室的工作[1-2]外,还未见其他报道。再生纤维素纤维及其混纺产品定性、定量分析方法——溶解法的研究开发,开辟了再生纤维素纤维间定性、定量分析方法的新途径。本文系对再生纤维素纤维定量分析方法——溶解法系列研究的补充,重点针对再生纤维素纤维之间定量分析的数据处理的深入分析研究,旨在进一步提高分析结果的准确性、精确性。本实验室研究发现,在再生纤维素纤维之间定量分析数据处理中采用传统给定一个损伤系数d值的方法不适用,采用标准曲线法能解决数据处理的问题。标准曲线法是分析数据中常见的方法,但是由于本文中的标准曲线法与一般的标准曲线法相比有相异和特殊之处,本文针对标准曲线法在再生纤维素纤维混纺产品成分分析数据处理应用中出现的几个问题及解决办法进行了阐述。
1 溶解法的标准曲线法
1.1 采用标准曲线法的必要性
本实验室所建立的用甲酸/氯化锌溶解法测定再生纤维素纤维混纺产品成分(如莱赛尔A100与竹纤维、莱赛尔A100与粘胶等)的方法是利用两者聚合度不同,在酸性溶剂中溶解能力的差异进行定量分析。由于莱赛尔A100与粘胶或者竹纤维的聚合度差异有限,此方法溶解机理造成莱赛尔A100在实验时会有小部分溶解损伤。以莱赛尔A100纤维与竹纤维分析数据为例,如图1所示:莱赛尔A100在甲酸/氯化锌溶液中不同浴比时,其损伤系数d值是不断变化的;而莱赛尔 A100含量不同时,相当于莱赛尔A100相应的浴比发生变化,其d值不同。图1中可见d值随浴比的增加而变大,且变化范围较大,同时实验条件的改变(如试剂、仪器、环境和人员操作)等因素也会引起其d值的改变。综合这两点考虑,传统给定一个d值的方法不适用于目前方法数据的计算。在实际数据处理中发现,采用以下标准曲线法能解决以上问题,即每个实验室每次测定首先确立自己的标准曲线,然后测定样品。
以 为y轴,
以
为y轴,
以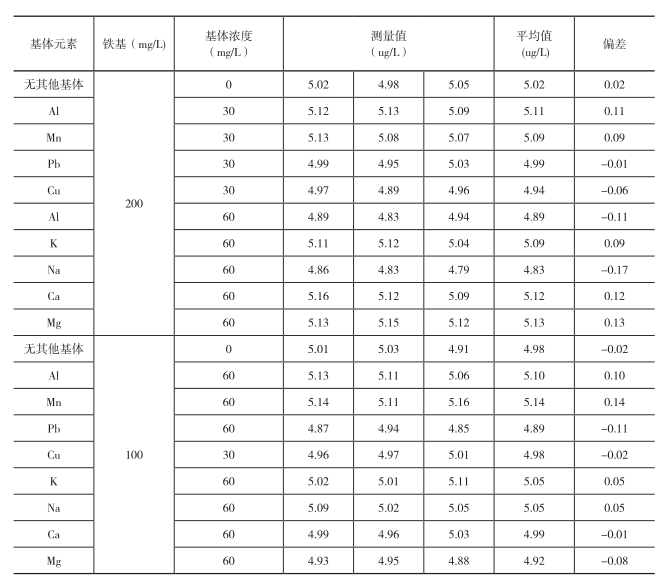 为x轴,那么此标准曲线的斜率为(1)式/(2)式的实质就是
k=
为x轴,那么此标准曲线的斜率为(1)式/(2)式的实质就是
k= 。由于在每个莱赛尔A100与其他再生纤维素纤维(如竹纤维或粘胶等)的溶解法分析条件确立时,在相应的分析条件下的其他再生纤维素纤维(如竹纤维或粘胶等)都已完全溶解,那么反应后剩余物净干质量即是反应后莱赛尔A100净干质量,这样带入式中可以看出,此标准曲线的斜率k值就是莱赛尔A100的损伤系数d值。
。由于在每个莱赛尔A100与其他再生纤维素纤维(如竹纤维或粘胶等)的溶解法分析条件确立时,在相应的分析条件下的其他再生纤维素纤维(如竹纤维或粘胶等)都已完全溶解,那么反应后剩余物净干质量即是反应后莱赛尔A100净干质量,这样带入式中可以看出,此标准曲线的斜率k值就是莱赛尔A100的损伤系数d值。
1.2 该标准曲线法的特点
由于此标准曲线法和平时很多浓度与响应值等的标准曲线法的共性和差异,标准曲线法中的一般注意事项适用于本方法,但也存在其自身的特点,现以莱赛尔A100与竹纤维定量分析的数据(见表1)为例说明。
(1)从理论上讲,标准曲线两端的实验点测量精密度较差,对标准曲线的残余偏差贡献大,对标准曲线的稳定性影响较大,尤其是高端的实验点变化对标准曲线的影响大[3]。在本标准曲线法中,由于纤维含量从100%~0%的范围较大,高端实验点(即100%,80%)的变化对标准曲线的影响见表2。表2采用表1中编号为1~9号的数据点拟合标准曲线,高含量数据点的权重过大,对线性方程的结果影响也大。如表2所示,如果所做标准曲线为非全含量范围(最大含量点为80%)时,只是去掉了100%的数据点,线性方程从y=1.1186x(R2=0.9999)(5%~100%)变成了y=1.1228x(R2=0.9999)(5%~80%)。当莱赛尔A100的100%和80%含量数据点d值较大时(表1中编号为3~11的数据点),60%及以下含量数据点相同,则其线性方程变为y=1.1242x(R2=1)(5%~100%)。由此可见,高端实验点(即100%,80%)数据的准确性直接影响标准曲线的k值大小,且影响较大。因此,本文建议在实验过程中,对于高浓度点(在全含量范围时就是莱赛尔A100含量在100%,80%等)可采取多次试验取平均的方法,这样可以避免一些误差。
此标准曲线法中全含量成分分析莱赛尔A100的含量为0%~100%,变化范围大,高含量实验点权重大,但低含量实验点权重小,5%、2%和1%的数据点对线性方程几乎无影响(见表2)。全含量范围拟合曲线时(最大为100%),可看出5%数据点的加入仅使线性方程由y=1.1185x(R2=0.9999)变成y=1.1186x(R2=0.9999)。但是含量再小的点,如2%和1%数据点的加入,虽然数据点本身d值很大(分别为1.187和1.193),但是对于该线性方程并无贡献,仍为y=1.1186x(R2=0.9999)。最大含量为80%时,情况类似(见表2)。
(2)采用标准曲线法测定样品时,应尽量用标准曲线的中间区域,因为中心点一定落在回归线上,此部分实验点的精密度相对较好[3]。从表3中可以看出,如果计算莱赛尔A100含量为30%左右的数据,那么选y=1.1297x(R2=1)(5%~60%)显然比y=1.1242x(R2=1)(5%~100%)要适合,因为前者的中间区域数据点刚好为30%左右。例如,莱赛尔A100的含量为60%的6个样品(见表4),分别按3组标准曲线数据[包括是否强制过零点,形成6个线性方程(5%~100%数据点所做)]计算后,其百分含量的偏倚率在-2.25%~0.51%。可见60%的样品由于使用标准曲线的中间区域,因此无论采用怎样的数据点得到不同斜率K的线性方程,标准曲线是否过原点,都对其计算结果影响不大,数据结果都较准确,准确度高于实际检测需求。
(3)针对低浓度实验点(以莱赛尔A100含量为5%为例)需标准曲线强制过原点,可减少计算结果误差[3](见表5)。由数据可见:同样的数据点拟合的标准曲线,5%样品用强制过零点的1、3、5式的计算结果的偏倚率在-3.41%~-0.32%;而用不强制过零点的2、4、6式计算结果的偏倚率在2.21%~9.63%。原因为:a) 本标准曲线法和平时很多浓度与响应值的标准曲线法不同,其斜率k值有其明确的实验意义。让标准曲线过零点,此处零点的意义为当莱赛尔A100纤维含量实验结果为0时,其计算结果为零,或者实际莱赛尔A100含量为0时,其实验结果也必然为0。b) 本身莱赛尔A100纤维含量5%为标准曲线最低端点,强制过零点等于增加了一个数据低点,即符合第二条。
(4)上述1和3的问题都是由于不同实验点的权重不同导致的,文献中有采用加权标准曲线法[4-6]、取对数回归标准曲线法[7-8](包括半对数和对数)来解决这类问题。本文中采用较容易操作的取对数方法进行数据处理。取对数方法的优点是可以降低高点的权重和影响力,使方程建立后对于高、低浓度点的权重合理,不同含量数据点的计算结果更准确[7]。即以ln()为y轴,ln()为x轴建立标准曲线,用表1中1~7的数据点和3~7、10、11的数据点分别做取对数的标准曲线,结果为:y=0.988x+0.1638(R2=1)和y=0.99x+0.1591(R2=1)计算同一组数据(5%、60%和100%)的误差,可见其偏倚率都在3%以内(分别为-1.52% ~ 2.42%,-1.84% ~ 2.60%)(见表6),莱赛尔A100的5%数据比强制过零点的普通标准曲线法的偏倚率还要小,符合实际分析需要。采用取对数的标准曲线法能在建立全含量(5% ~ 100%)的标准曲线的情况下,保证高、低含量数据点的误差都小,解决了上述1和3的问题(见表6)。
2 结论
采用标准曲线法能避免传统给定一个损伤系数d值的方法中由于实验条件的变化引起d值变化的缺点,但在使用中应注意以下几点:
(1)高浓度点取多次试验中靠近其平均d值的数据点建立曲线更准确。
(2)采用标准曲线中间区域计算数据更准确。
(3)低含量数据点的计算可采用强制过零点,使结果更准确。
(4)采用对数法回归建立标准曲线,可以一次建立全含量范围的标准曲线方程,使各浓度点的权重合理,并且高、低浓度点的结果都计算准确。
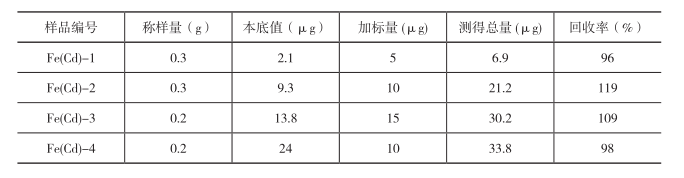
图1 浴比与莱赛尔A100纤维的损伤系数d值的关系
表1 不同莱赛尔A100/竹纤维含量实验数据表
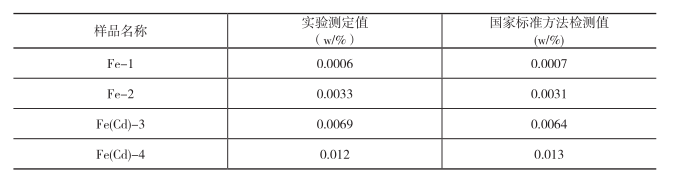
表2 莱赛尔A100的100%和80% d值较小时不同数据点拟合的线性方程

表3 莱赛尔A100的100%和80% d值较大时不同数据点拟合的线性方程

表4 莱赛尔A100含量为60%的样品用不同标准曲线计算结果

注1:式1 y=1.1242x,2 y=1.1198x+0.2777,3 y=1.1195x,4 y=1.1105x+0.5568,5 y=1.1186x,6 y = 1.1115x + 0.4363。
注2:
表5 莱赛尔A100含量为5%的样品用不同标准曲线计算结果

 注1:式1 y=1.1242x,2 y=1.1198x+0.2777,3 y=1.1195x,4 y=1.1105x+0.5568,5 y=1.1186x,6 y = 1.1115x + 0.4363。
注1:式1 y=1.1242x,2 y=1.1198x+0.2777,3 y=1.1195x,4 y=1.1105x+0.5568,5 y=1.1186x,6 y = 1.1115x + 0.4363。
注2:
表6 莱赛尔A100含量为5%、60%和100%数据用取对数法的计算结果

参考文献
[1]赵素敏,高友军,刘锦瑞,等.莱赛尔A100与竹纤维混纺产品纤维成分定量分析[J].印染, 2017, 43(3):50-53.
[2]刘锦瑞,张向丽,高友军,等.染色莱赛尔纤维/粘胶纤维混纺产品的定量分析[J].印染, 2017, 43(2):46-49.
[3]邓勃.关于校正曲线建立和应用中一些问题的探讨[J].中国无机分析化学, 2011, 1(3):1-7.
[4]钟大放.以加权最小二乘法建立生物分析标准曲线的若干问题[J].药物分析杂志, 1996, 16(5):343-346.
[5]商庆节,吴玲,罗涟荣,等.SPSS在生物分析测定过程中计算加权标准曲线的应用[J].数理医药学杂志, 2013, 26(3):356-357.
[6]郑锦文,黄凤妹.加权最小二乘法建立皮革中游离甲醛含量分析标准曲线的研究[J].西部皮革, 2013, 35(10):46-47,57.
[7]余建兵.品红亚硫酸法测定酒中甲醇的标准曲线绘制法的探讨[J].计量与测试技术, 2003, 3:42-43.
[8]汤权,刘秀兰,郑春早.半对数回归在测定麻疹及风疹病毒抗体水平中的应用[J].现代预防医学, 2007, 34(6):1058-1060.







