CopyRight 2009-2020 © All Rights Reserved.版权所有: 中国海关未经授权禁止复制或建立镜像
浅谈容量计重中常用的密度温度系数和体积温度系数
作者:孙浩平1
孙浩平1
摘 要 本文以纯水为例,介绍了确定液态物质密度温度系数和体积温度系数的一种方法,并分析了该方法产生的误差。用这一方法确定的精炼棕榈油的密度温度系数更加合理。
关键词 容量计重;密度温度系数;体积温度系数
A Discussion on Density Temperature Factor and Volume Temperature Factor Used in Volumetric Survey
SUN Hao-Ping1
Abstract In this paper, a method is illustrated by the example of water for the determination of the density temperature factor and volume temperature factor of the liquid substances, and the error incurred is analyzed. The study shows that the density temperature factor of RBD palm oil determined by this method will be more reasonable.
Keywords Volumetric survey; density temperature factor; volume temperature factor
针对液体化工品和动植物油脂的容量计重,常要用到密度温度系数和体积温度系数。1986年,原辽宁进出口商品检验局将日本海事鉴定协会与新日本检定协会发布的内含这两个系数的化工品系数表引入我国,并给出了动植物油脂的密度温度系数的取值[1];1991年,汤宏兵等给出了这两个系数的定义[2]:液体温度每变化1℃其密度的变化值称为密度温度系数,液体温度每变化1℃其体积的变化率称为体积温度系数;1997年,张鹤卿等给出了这两个系数的公式表示[3]:
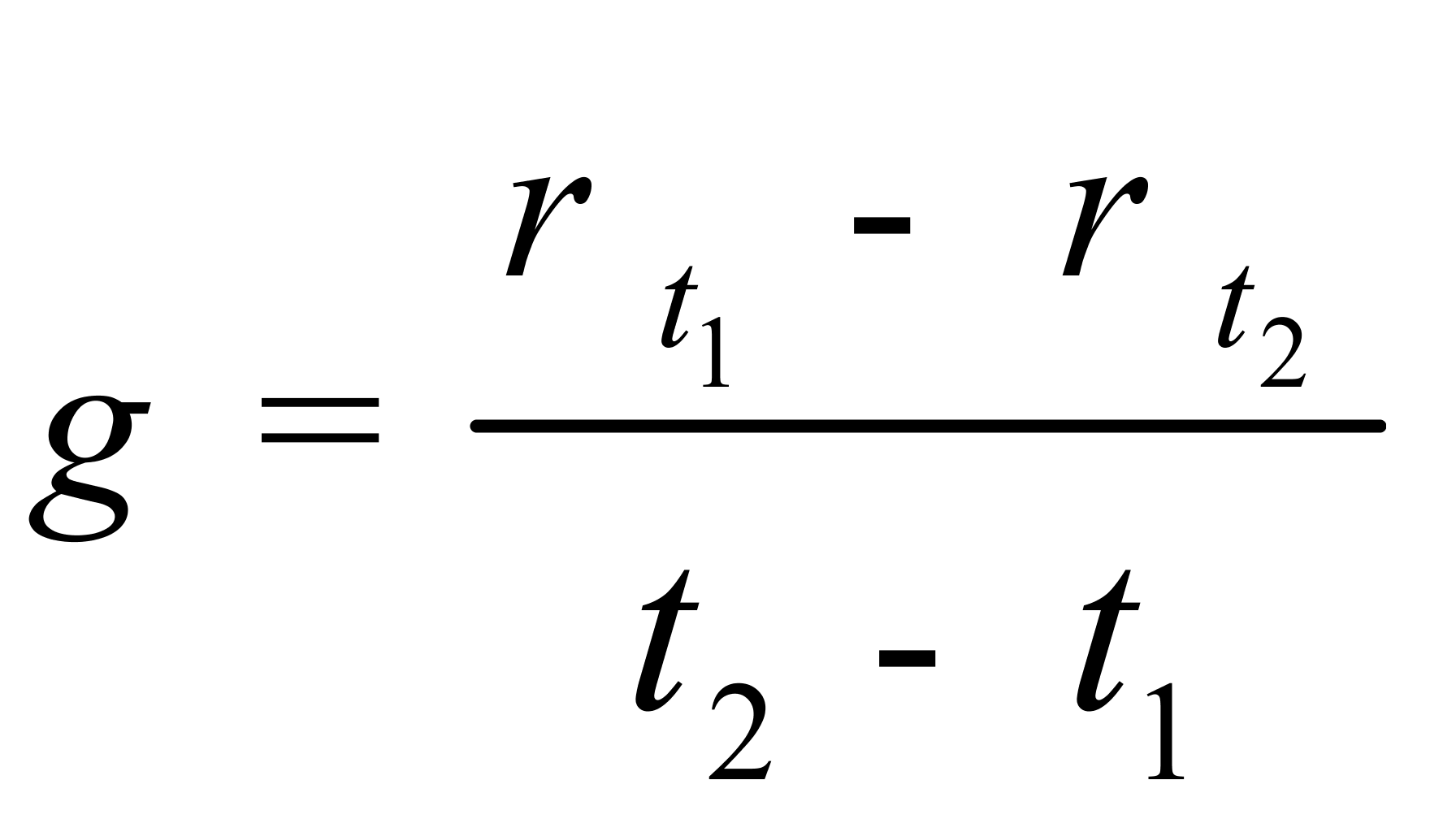 (1)
(1)
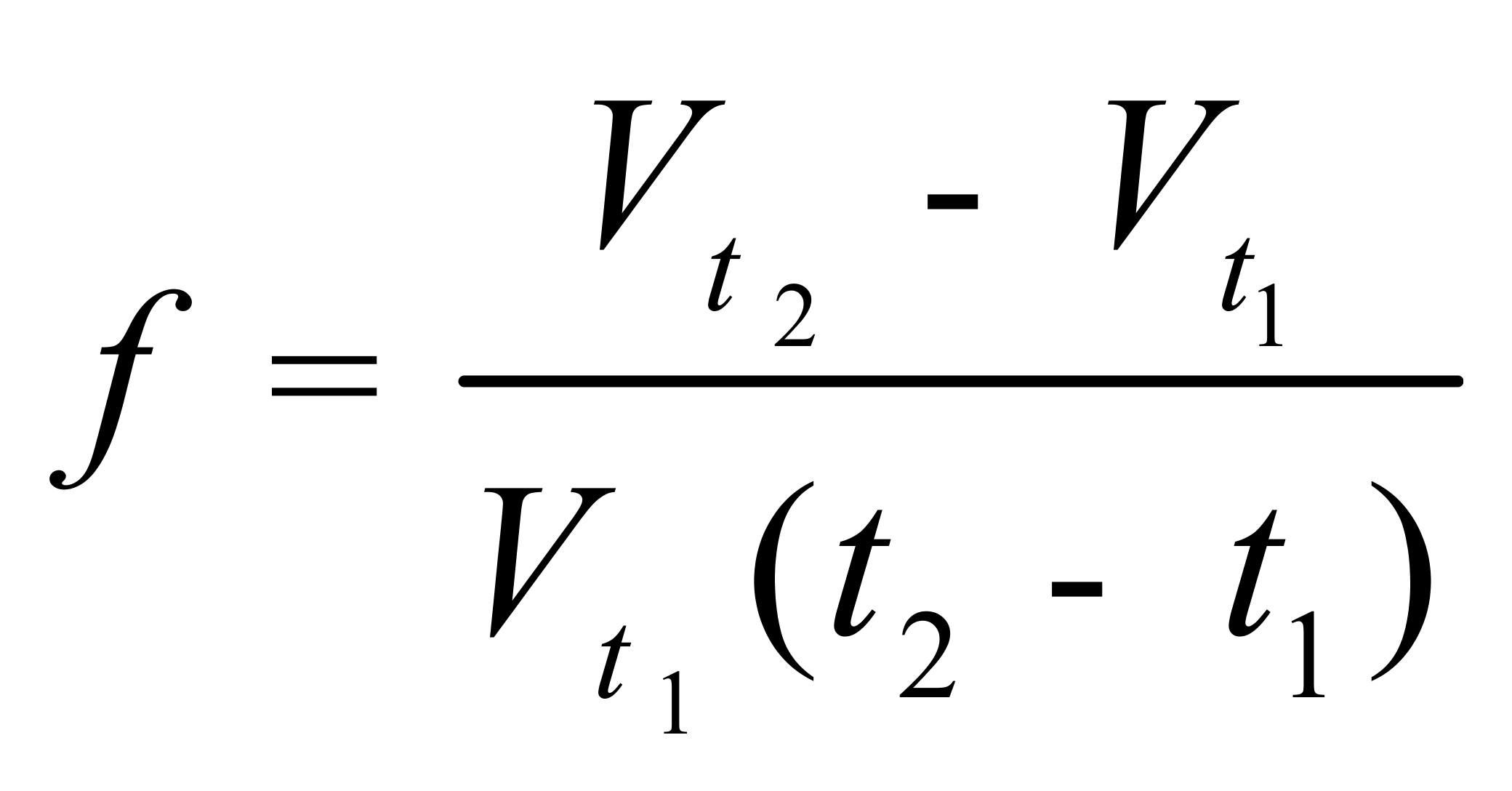 (2)
(2)
式中:
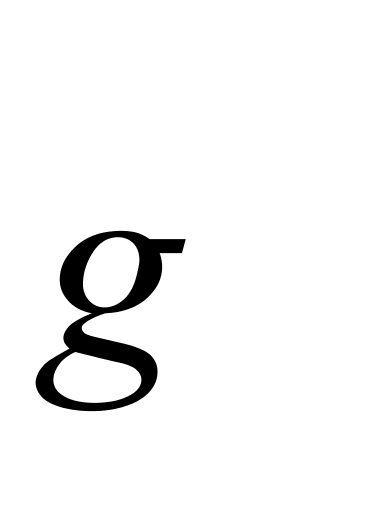 ——液体的密度温度系数,kg/(m3·℃);
——液体的密度温度系数,kg/(m3·℃);
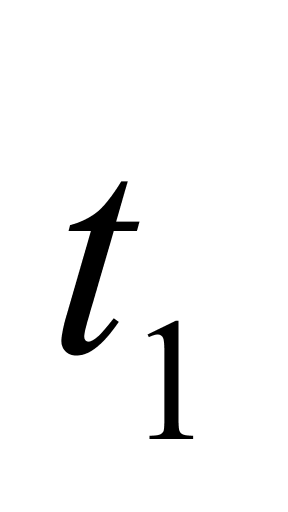 、
、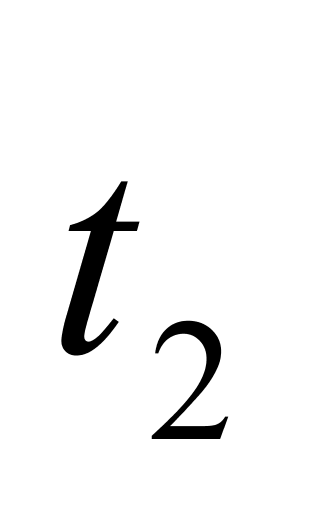 ——液体的初始温度和变化后的温度,℃;
——液体的初始温度和变化后的温度,℃;
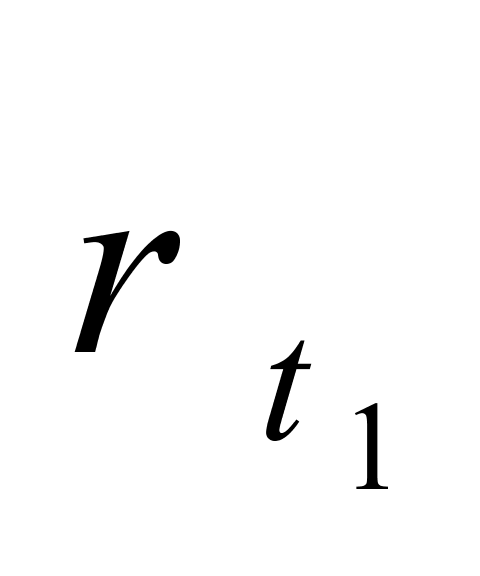 、
、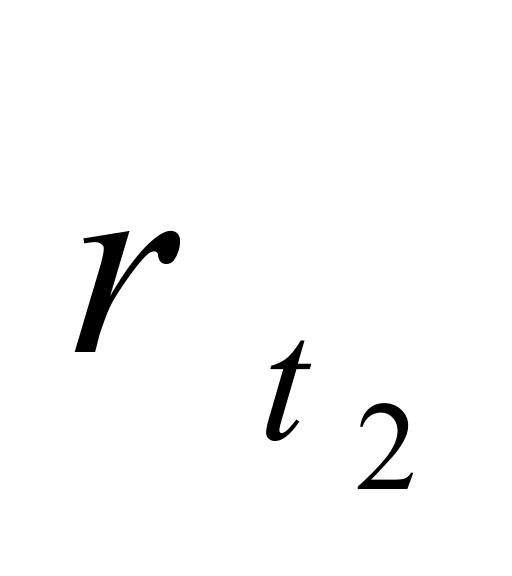 ——液体分别在温度为
——液体分别在温度为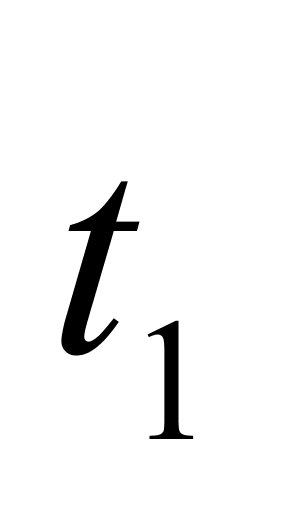 和
和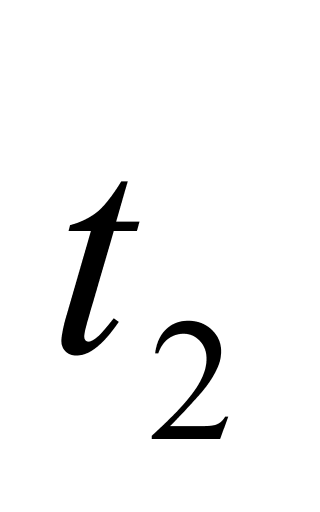 时的密度,kg/m3;
时的密度,kg/m3;
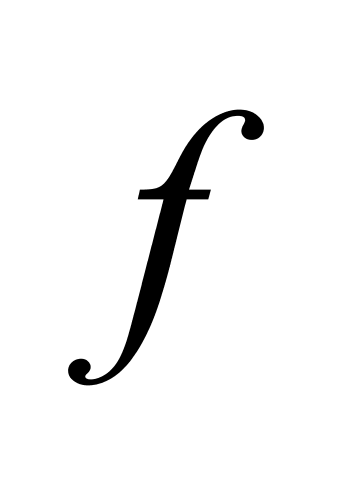 ——液体的体积温度系数,℃-1;
——液体的体积温度系数,℃-1;
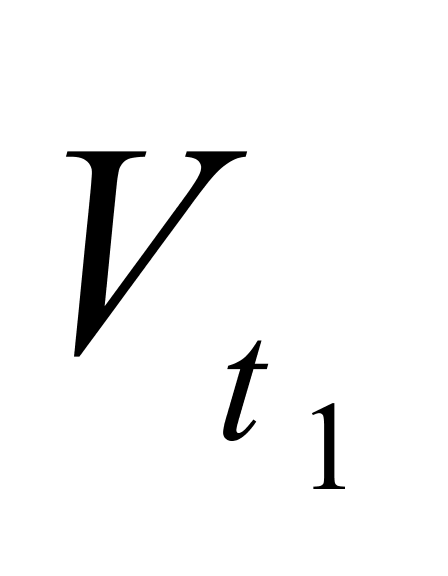 、
、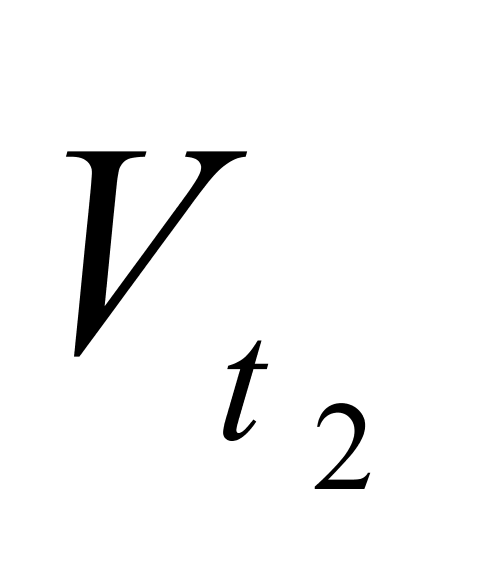 ——液体分别在温度为
——液体分别在温度为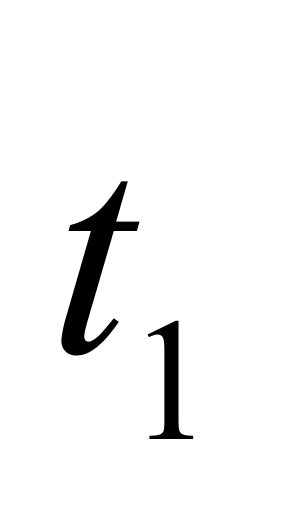 和
和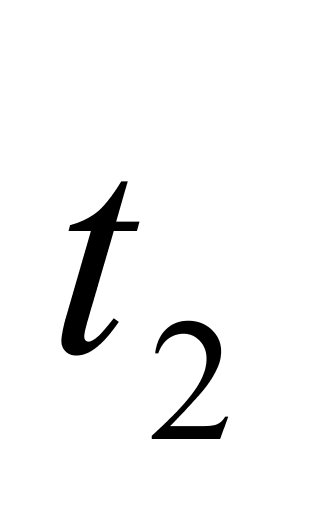 时的体积,m3。
时的体积,m3。
并证明了:
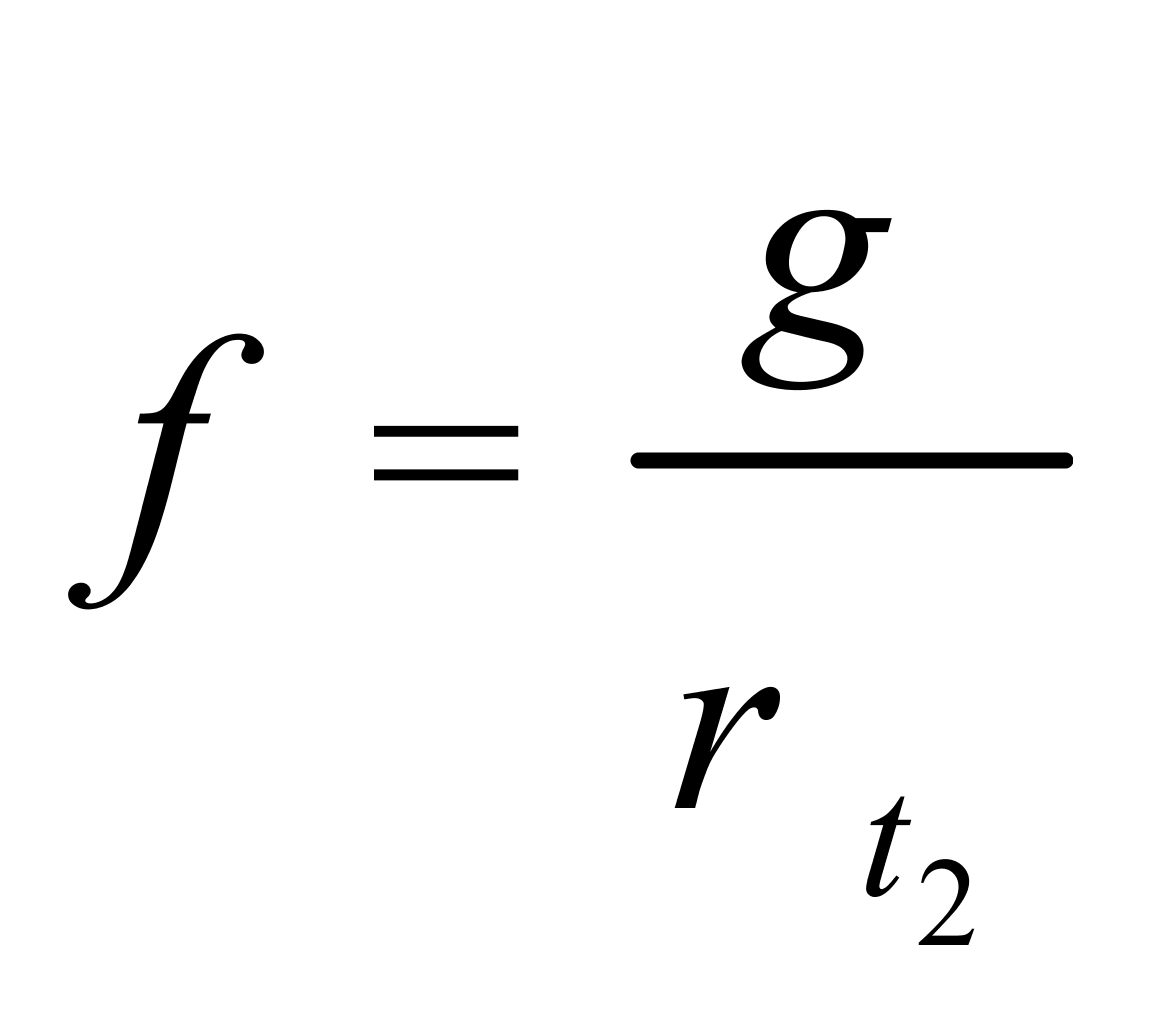 (3)
(3)
从严格意义上讲,液体的密度与温度并不呈线性关系。因此,前述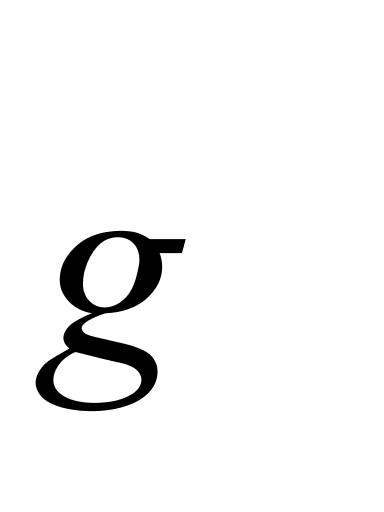 和
和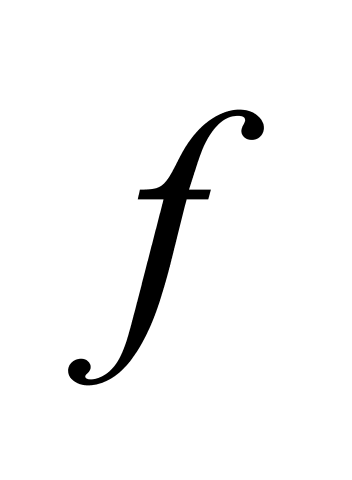 应加下标“
应加下标“ ”[4],即(1)式和(2)式应分别改写为:
”[4],即(1)式和(2)式应分别改写为:
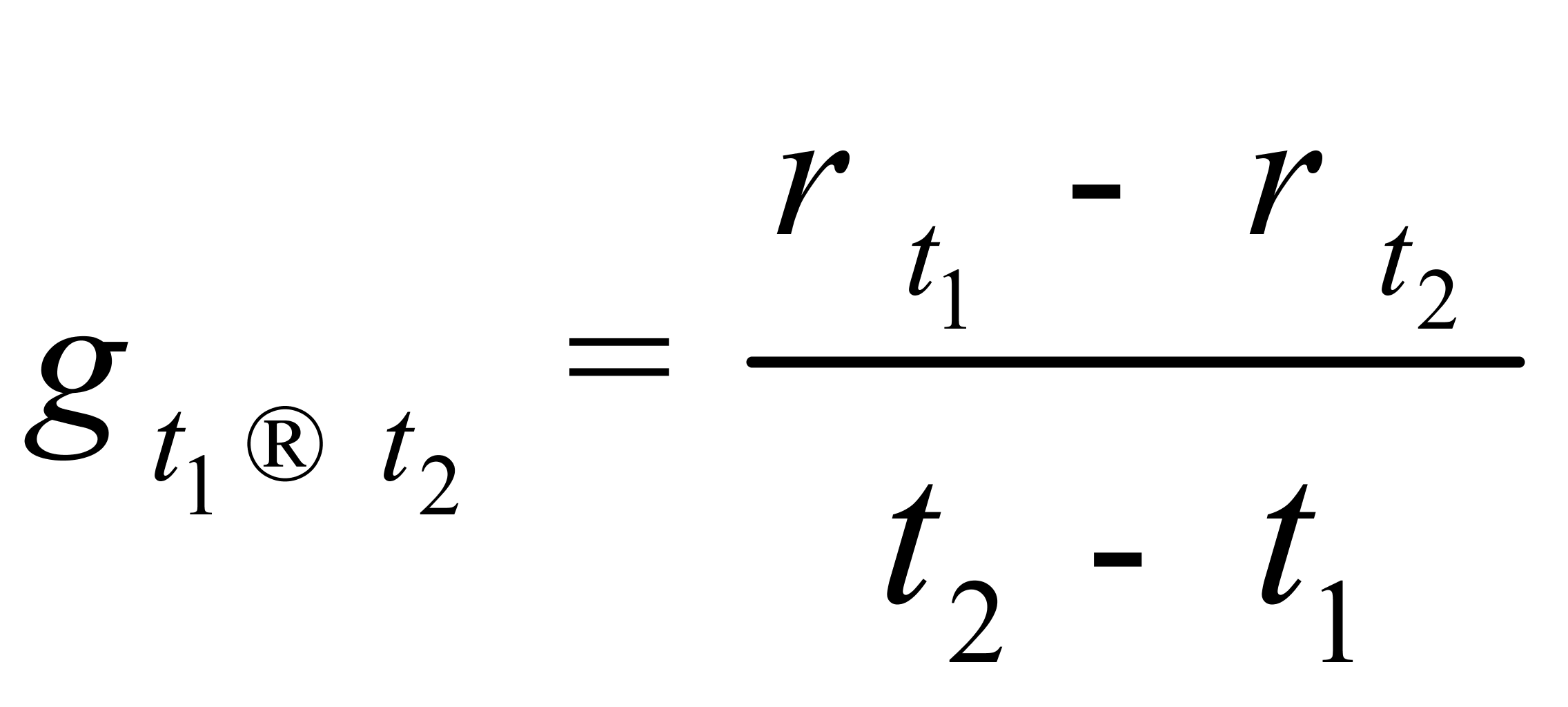 (4)
(4)
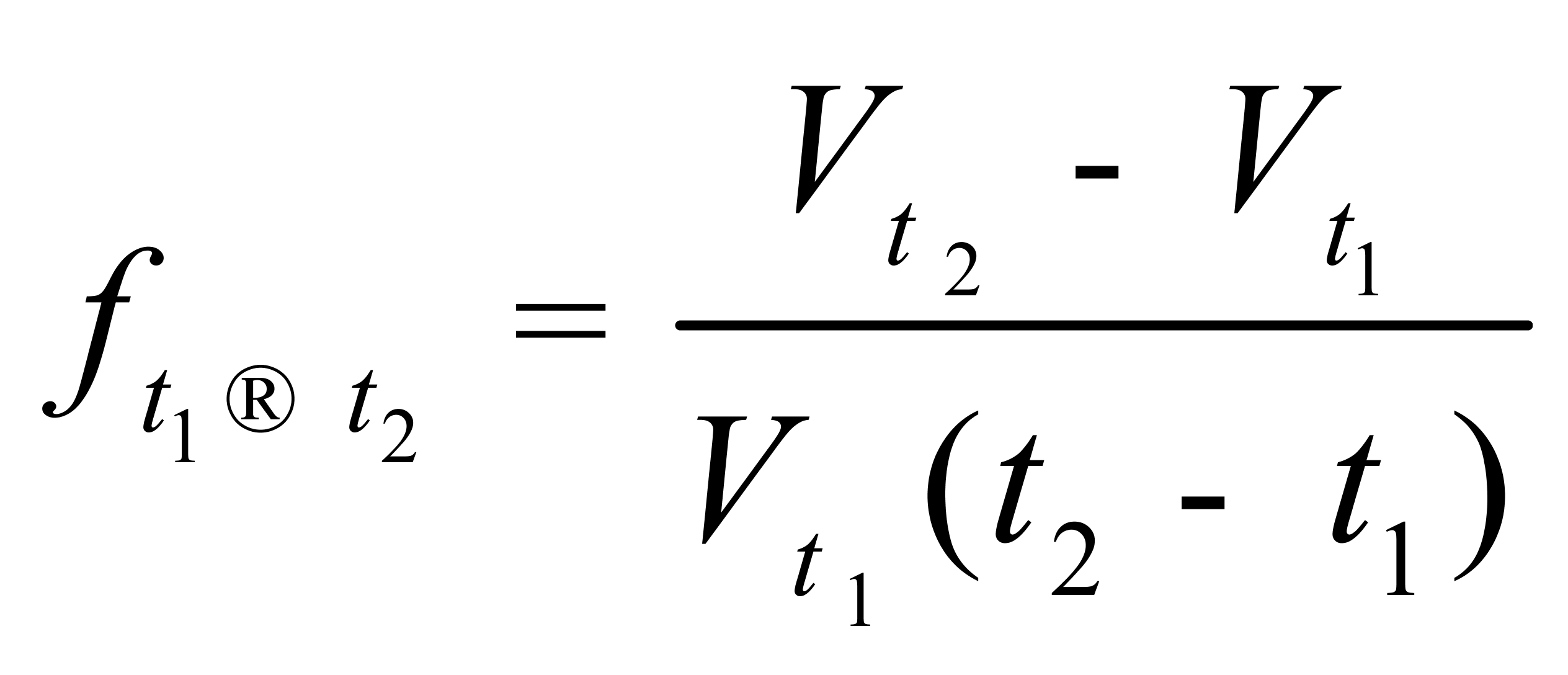 (5)
(5)
式中:
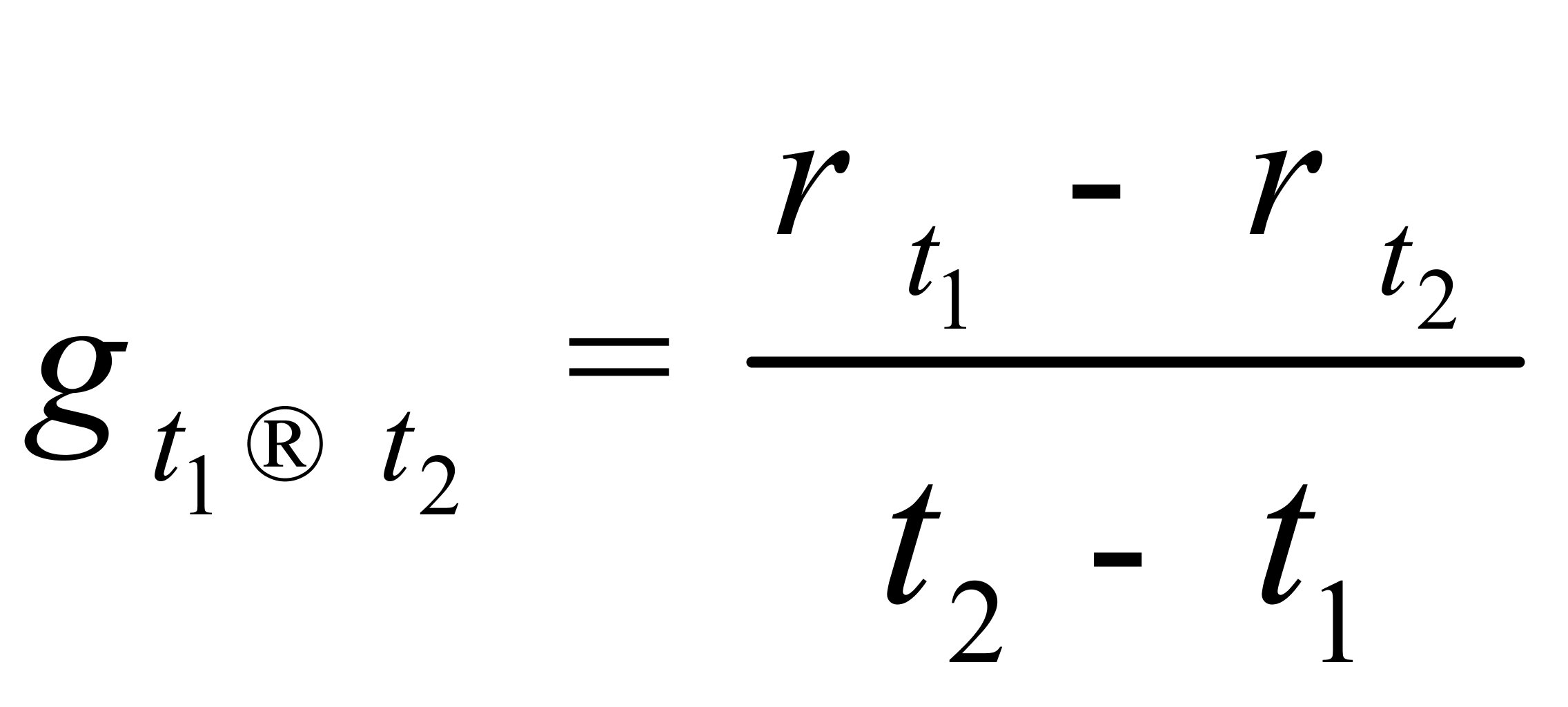 ——液体从初始温度t1变化到t2时的密度温度系数,kg/(m3·℃);
——液体从初始温度t1变化到t2时的密度温度系数,kg/(m3·℃);
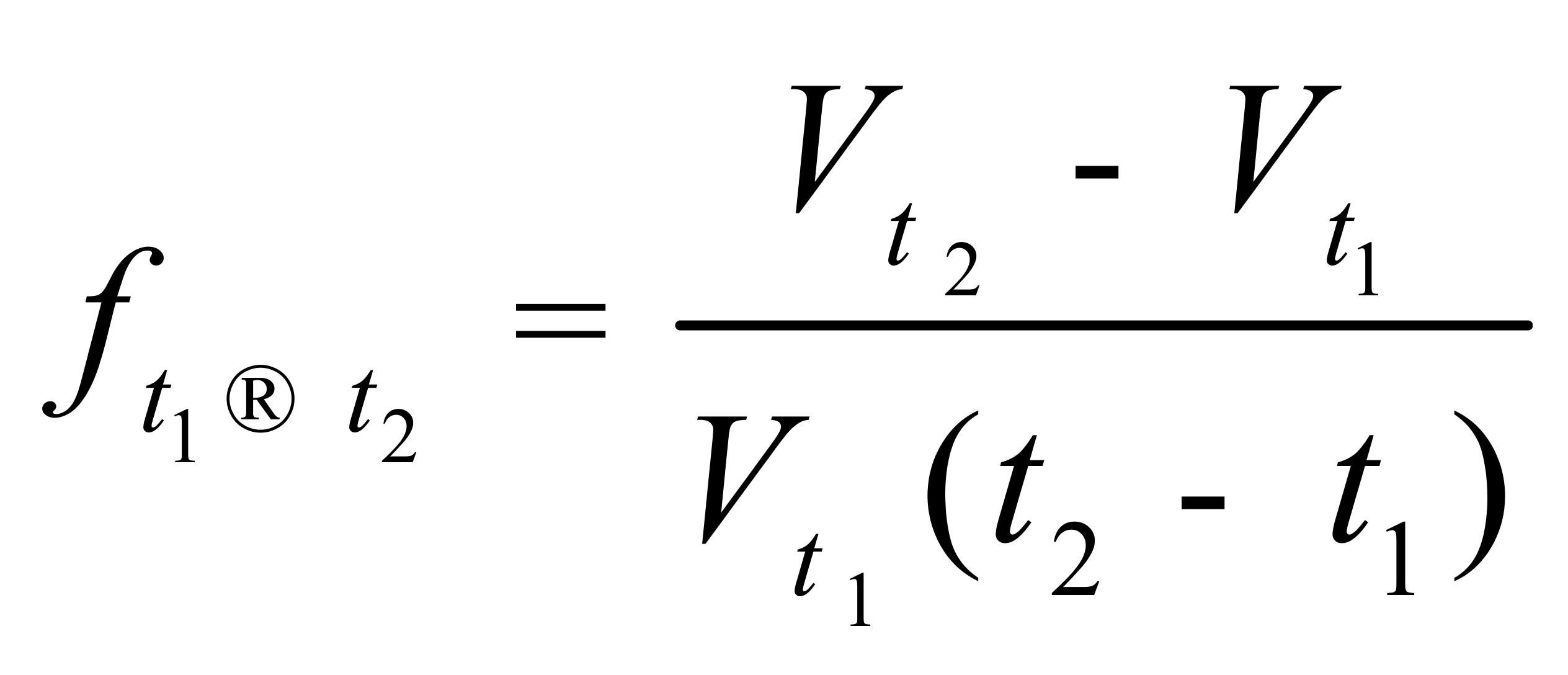 ——液体从初始温度t1变化到t2时的体积温度系数,℃-1。
——液体从初始温度t1变化到t2时的体积温度系数,℃-1。
进而,(3)式相应地改写为:
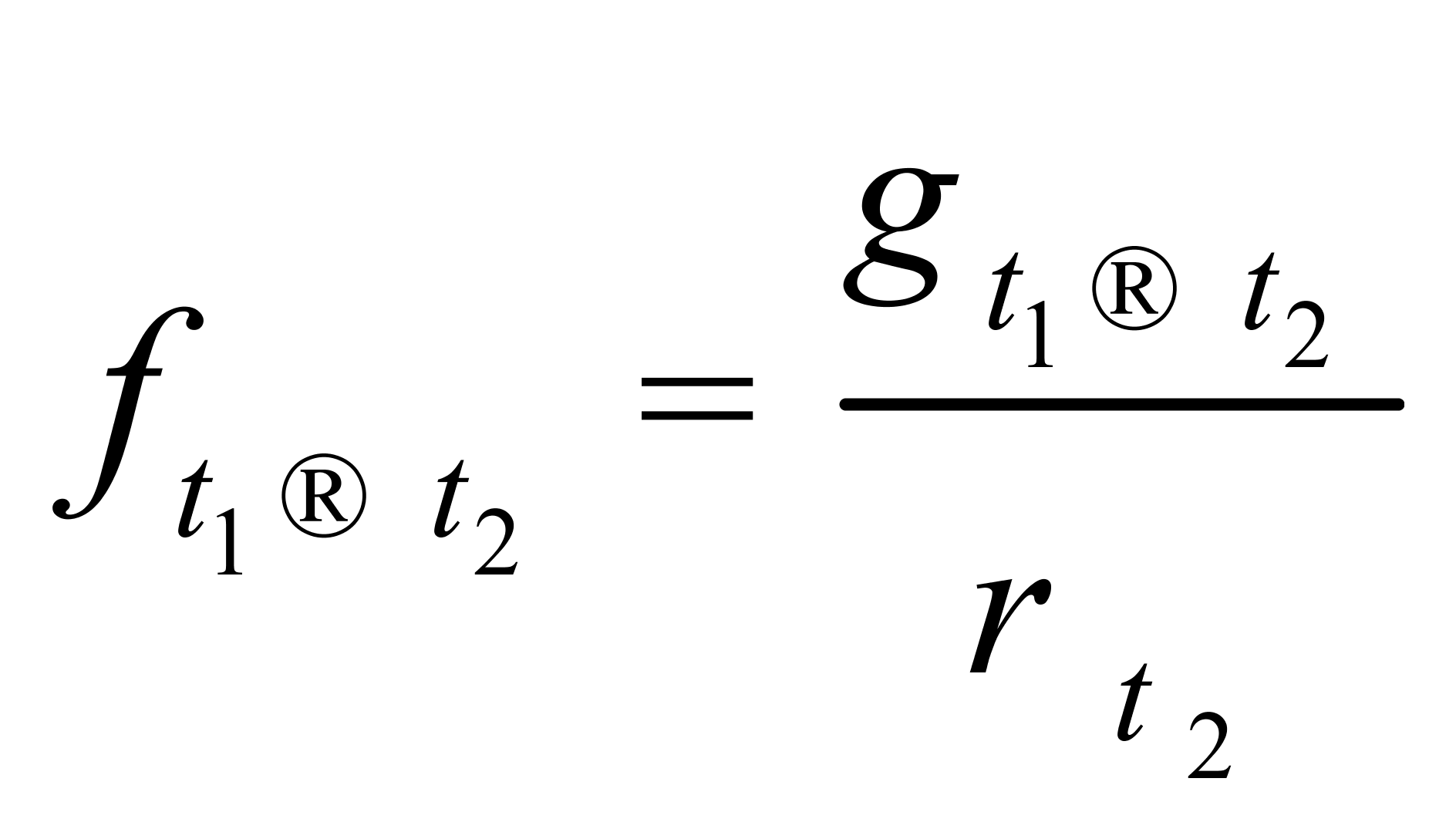 (6)
(6)
由(4)式,显然有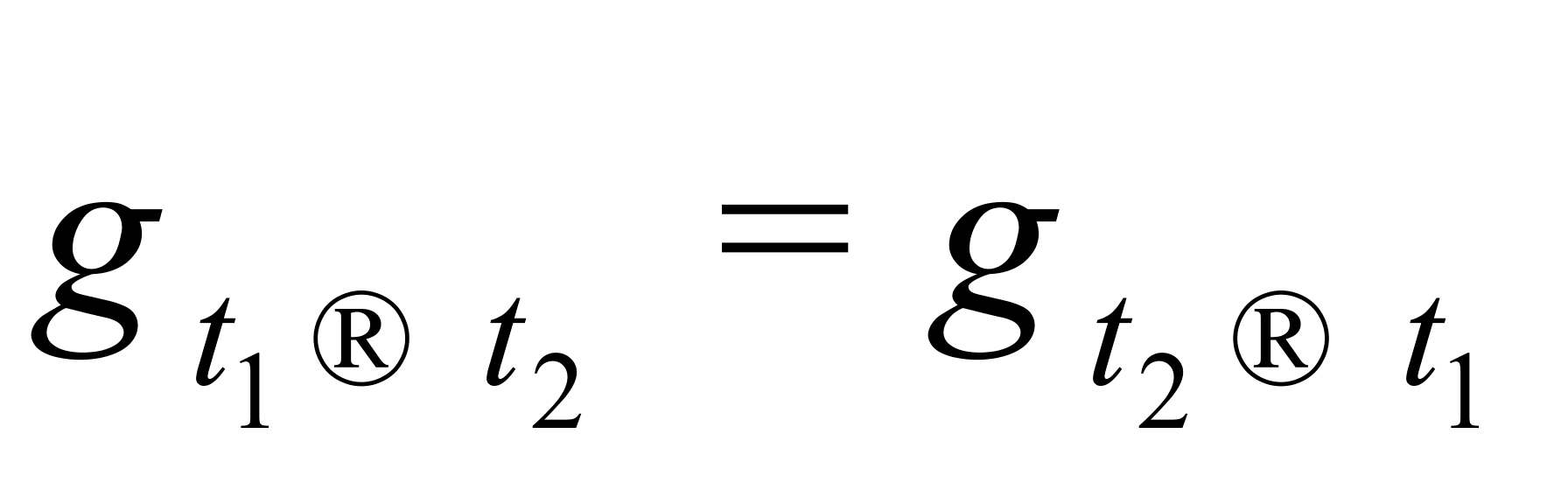 ,但由(5)式,一般得不到
,但由(5)式,一般得不到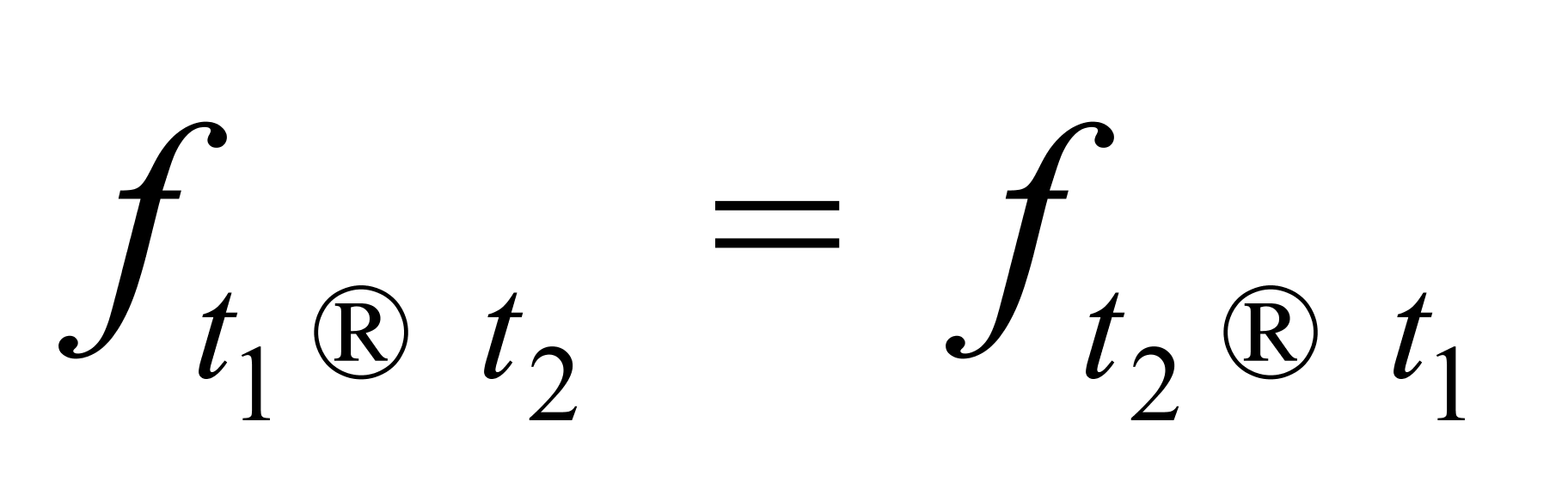 。
。
目前,国内一直沿用日本海事鉴定协会与新日本检定协会发布的化工品系数表[5],动植物油脂的密度温度系数则规定除鱼油的为0.68 kg/(m3·℃)外,其他的均为0.64 kg/(m3·℃) [6]。但是,对于液态物质密度温度系数和体积温度系数的确定方法,国内尚未检索到相关介绍;对于前述化工品系数表的适用范围,以及动植物油脂的密度温度系数的取值也还存在一些争议[7]。
1 纯水密度温度系数与体积温度系数的探讨
Cailletet-Mathias直径线法则[8]揭示了液态物质的密度随温度的变化关系曲线相似于抛物线,图1所显示的纯水密度①与温度的关系曲线印证了这一点。
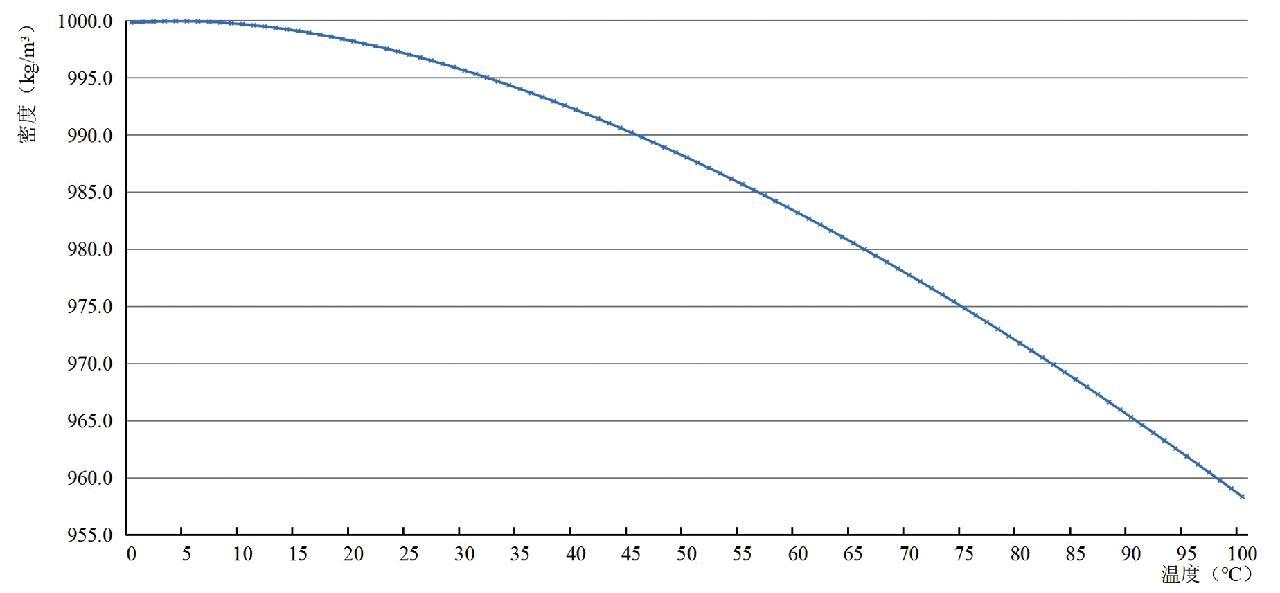
图1 纯水密度与温度(0℃~100℃)关系曲线
Fig.1 Density-temperature (0℃~100℃) curve of water
下面就以纯水为例,探讨液态物质的密度温度系数与体积温度系数的确定方法,并详细分析用所确定的这两个系数值进行重量计算将产生的误差。
基于容量计重中实际计算的需要,本文将纯水的基准温度②t0分为15℃和20℃两种,将拟探讨的纯水的温度区间设定为10℃~30℃。图2中的蓝色曲线显示了纯水在10℃~30℃温度区间内其密度与温度的关系。
使用最小二乘法可得到10℃~30℃温度区间内(温度间隔设为5℃)纯水密度的线性回归方程:
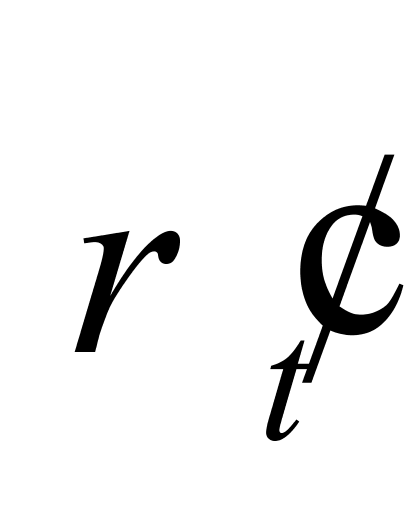 = -0.203268t+1002.00692(7)
= -0.203268t+1002.00692(7)
式中:
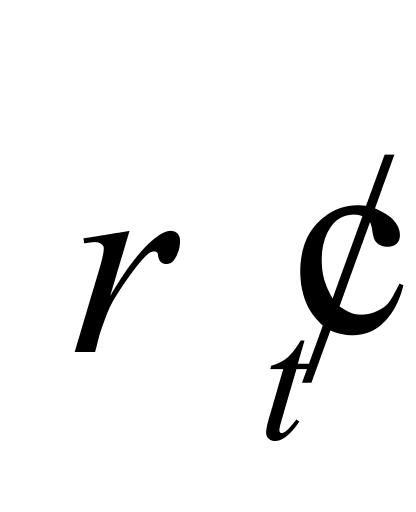 ——通过线性回归得到的纯水密度,kg/m3;
——通过线性回归得到的纯水密度,kg/m3;
t ——纯水温度,℃,这里取10℃~30℃。
此外,可以计算出纯水密度与温度的相关系数r=-0.99,r2=0.98。后者很接近于1,说明纯水的密度与温度具有很好的线性相关性,(7)式可用来估计纯水在10℃~30℃温度区间内的密度值。图2中深红色的线段即表示通过(7)式得到的纯水密度与温度的关系(具体数据见表1)。
现分别用任意温度“t”和基准温度“t0”代替(4)式、(5)式和(6)式中的“t1”和“t2”,得:
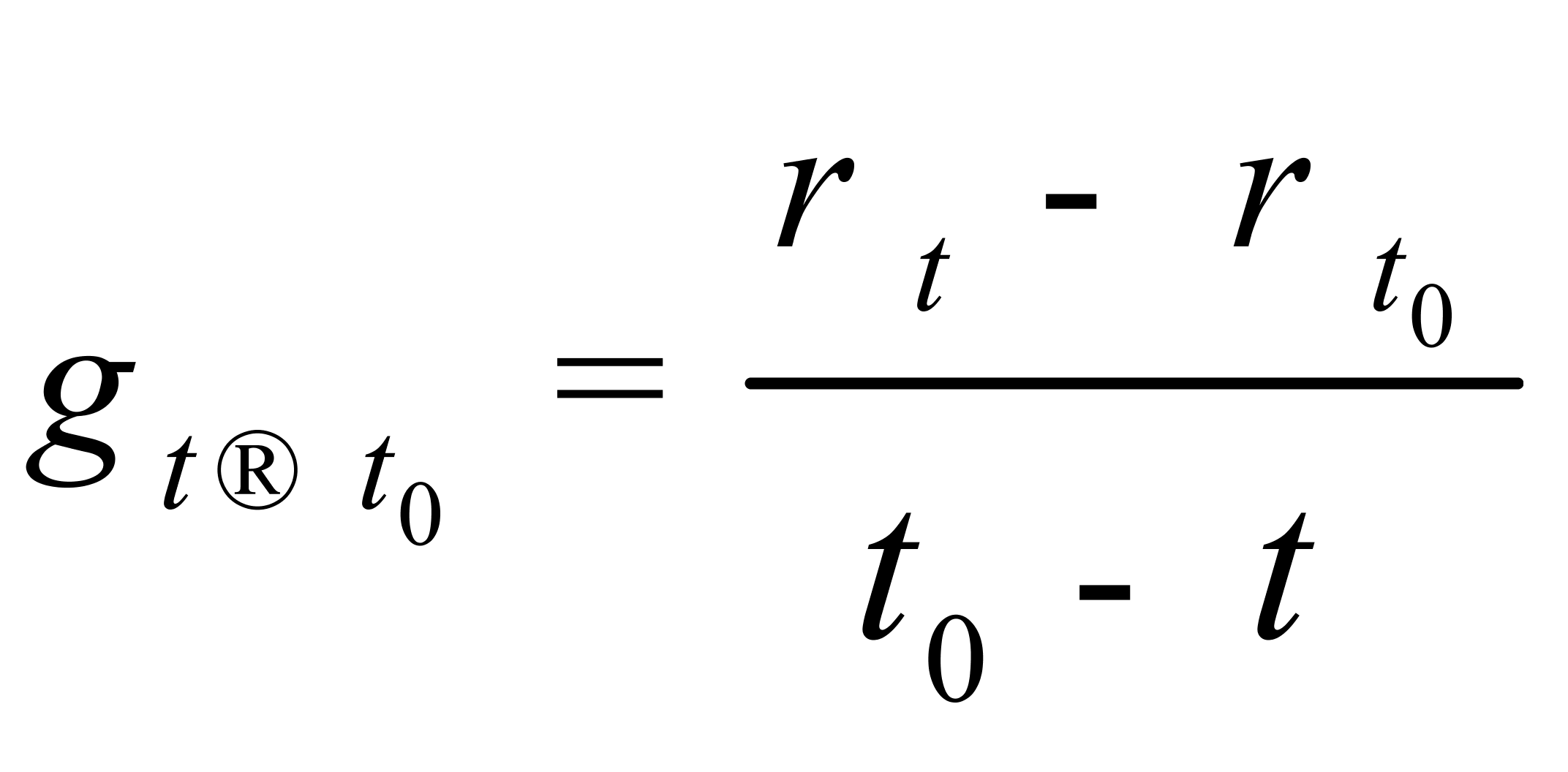 (8)
(8)
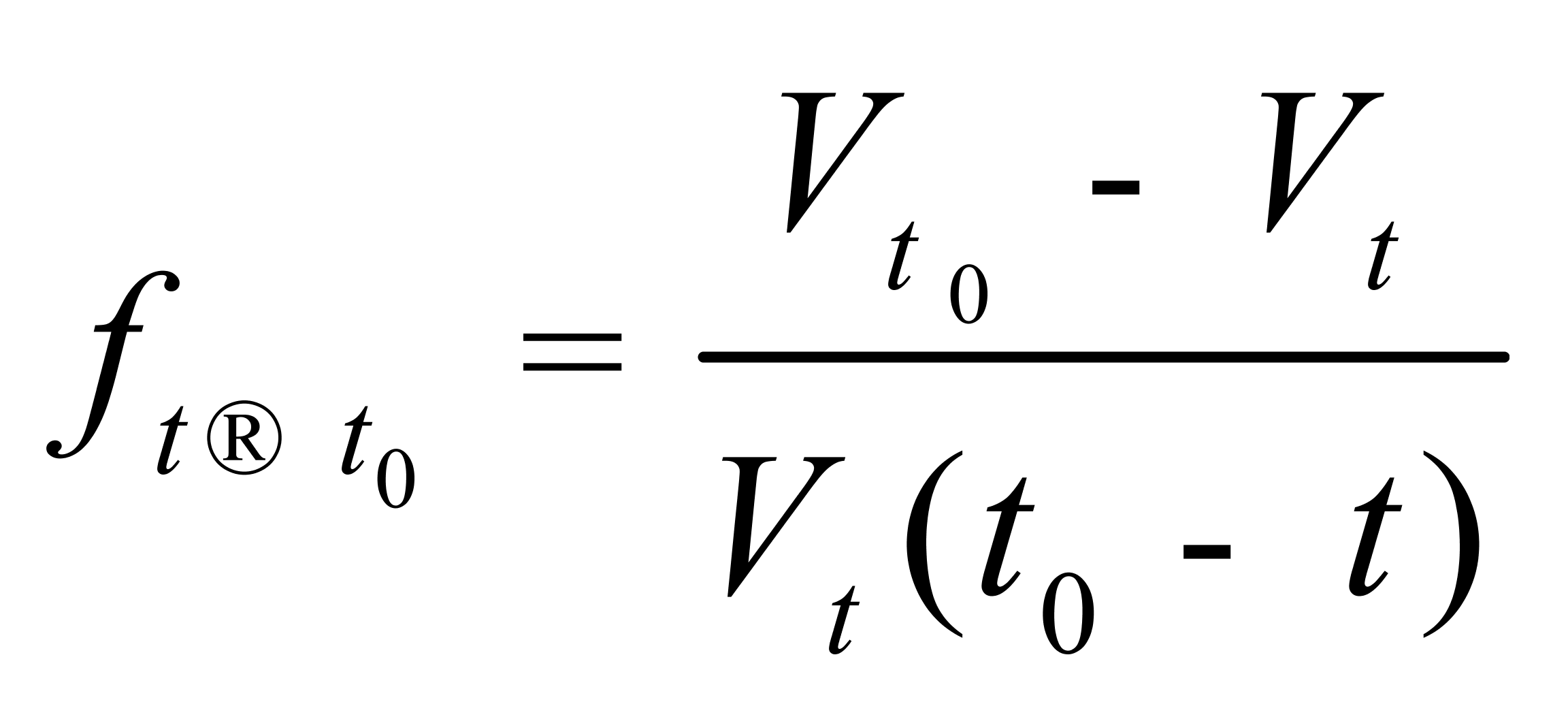 (9)
(9)
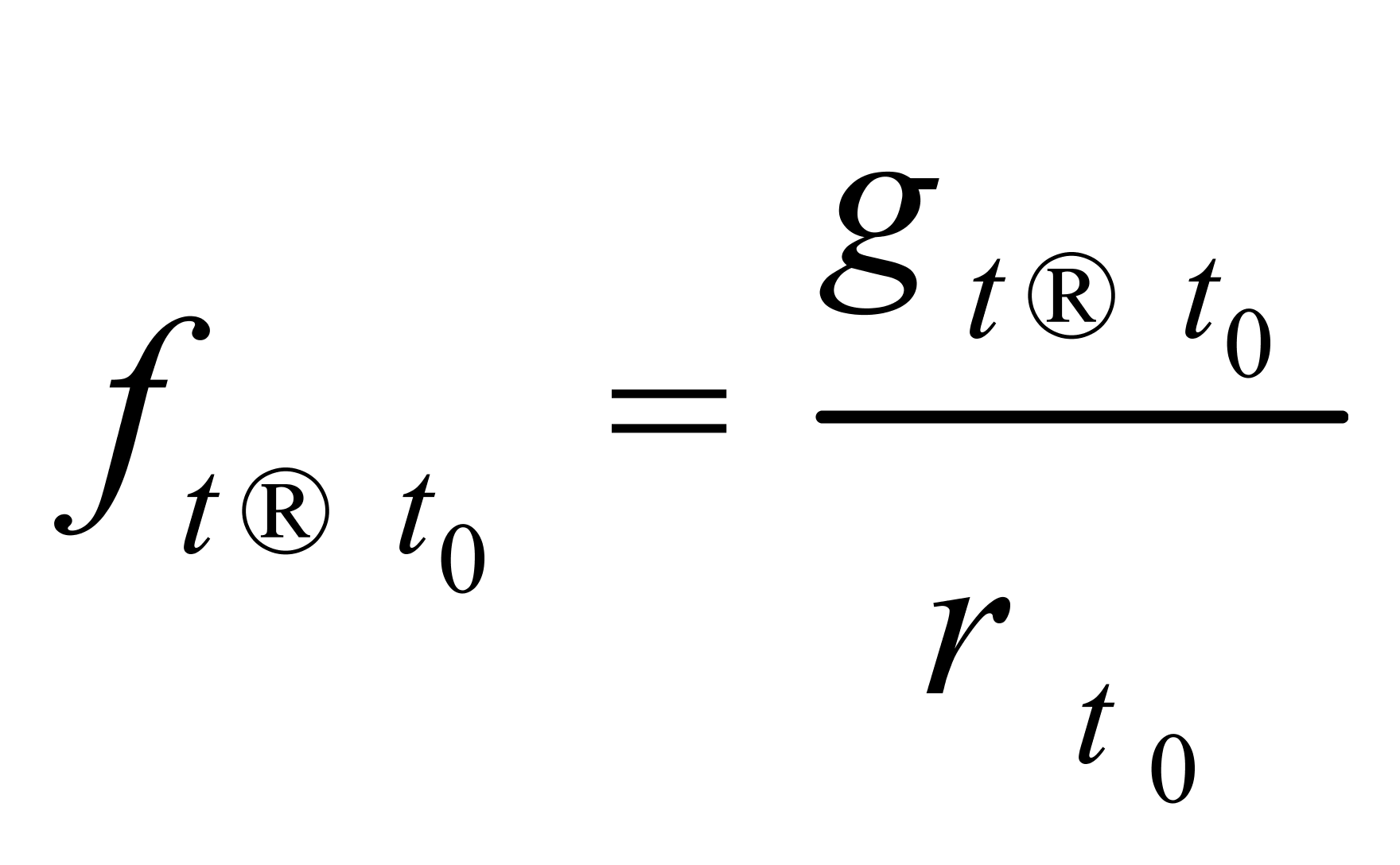 (10)
(10)
根据(8)式和(10)式可计算出纯水在10~30℃温度区间内各个温度间隔点(温度间隔设为5℃)的密度温度系数与体积温度系数,表2显示了较为详细的计算结果。
表1 通过(7)式线性回归得到的密度与利用(11)式反推得到的密度之比较
Table 1 Comparative results of density calculated by formula (7) and (11)
℃ | kg/m3 | kg/m3 | ‰ | kg/m3 | ‰ |
10.0 | 999.7027 | 999.9742 | 0.2716 | 1000.2067 | 0.5041 |
11.0 | 999.6081 | 999.7710 | 0.1630 | 1000.0067 | 0.3988 |
12.0 | 999.5005 | 999.5677 | 0.0672 | 999.8067 | 0.3064 |
13.0 | 999.3801 | 999.3644 | -0.0157 | 999.6067 | 0.2267 |
14.0 | 999.2474 | 999.1612 | -0.0863 | 999.4067 | 0.1594 |
15.0 | 999.1026 | 998.9579 | -0.1448 | 999.2067 | 0.1042 |
16.0 | 998.9459 | 998.7546 | -0.1915 | 999.0067 | 0.0609 |
17.0 | 998.7778 | 998.5514 | -0.2267 | 998.8067 | 0.0289 |
18.0 | 998.5984 | 998.3481 | -0.2507 | 998.6067 | 0.0083 |
19.0 | 998.4079 | 998.1448 | -0.2635 | 998.4067 | -0.0012 |
20.0 | 998.2067 | 997.9416 | -0.2656 | 998.2067 | 0.0000 |
21.0 | 997.9950 | 997.7383 | -0.2572 | 998.0067 | 0.0117 |
22.0 | 997.7730 | 997.5350 | -0.2385 | 997.8067 | 0.0338 |
23.0 | 997.5408 | 997.3318 | -0.2095 | 997.6067 | 0.0661 |
24.0 | 997.2988 | 997.1285 | -0.1708 | 997.4067 | 0.1082 |
25.0 | 997.0470 | 996.9252 | -0.1222 | 997.2067 | 0.1602 |
26.0 | 996.7857 | 996.7220 | -0.0639 | 997.0067 | 0.2217 |
27.0 | 996.5151 | 996.5187 | 0.0036 | 996.8067 | 0.2926 |
28.0 | 996.2353 | 996.3154 | 0.0804 | 996.6067 | 0.3728 |
29.0 | 995.9465 | 996.1121 | 0.1663 | 996.4067 | 0.4621 |
30.0 | 995.6488 | 995.9089 | 0.2612 | 996.2067 | 0.5603 |
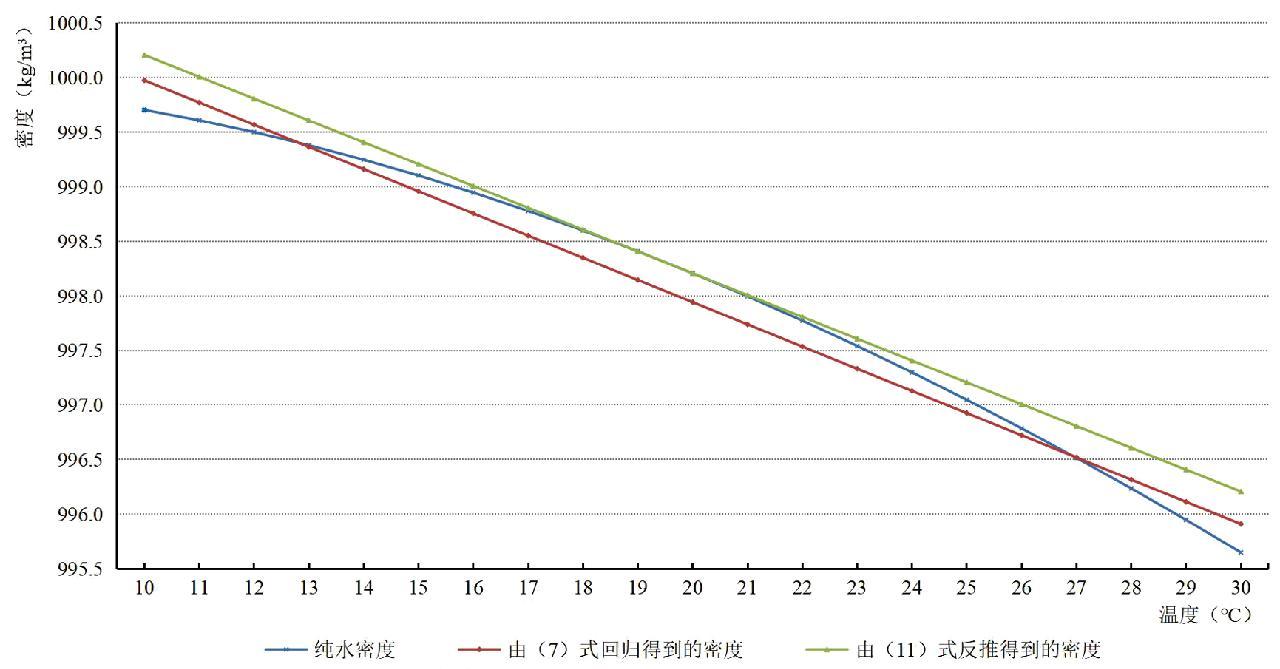
图2 纯水密度与温度 (10~30℃) 关系曲线
Fig.2 Density-temperature (10~30℃) curve of water
表2 纯水密度温度系数与体积温度系数计算表
Table 2 Work sheet for the density temperature factor and volume temperature factor of water
℃ | kg/m3 | kg/(m3·℃) | ℃-1 | kg/(m3·℃) | ℃-1 |
10 | 999.7027 | 0.149600 | 0.000149869 | 0.120020 | 0.000120128 |
15 | 999.1026 | 0.179180 | 0.000179502 | / | / |
20 | 998.2067 | / | / | 0.179180 | 0.000179341 |
25 | 997.0470 | 0.231940 | 0.000232357 | 0.205560 | 0.000205745 |
30 | 995.6488 | 0.255790 | 0.000256250 | 0.230253 | 0.000230460 |
均值 | 修约前 | 0.204128 | 0.000204494 | 0.183753 | 0.000183918 |
修约后 | 0.20 | 0.00020 | 0.18 | 0.00018 |
从表2可以看出,纯水的密度温度系数和体积温度系数均不是常数,且随着温度的升高,这两个系数值会逐渐增大;此外,对于不同的基准温度,相应的系数值也不一样。
在容量计重工作中,我们当然可以像编制石油计量表一样,针对不同的液体化工品分别编制一个详细的系数表;或者把温度区间缩小,然后对每一个较小的温度区间分别给定一个系数值。但这会大幅增加测定密度的工作量,同时也不便于日常使用。接下来的误差分析表明没有这个必要。
表2最后两行列出了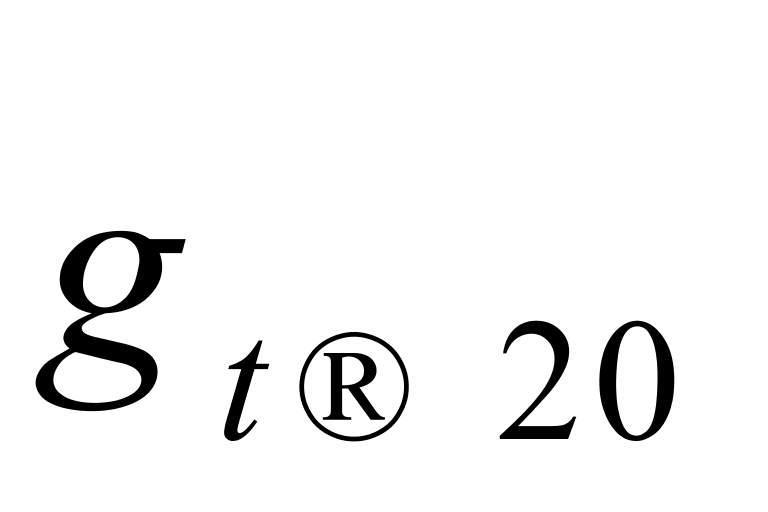 、
、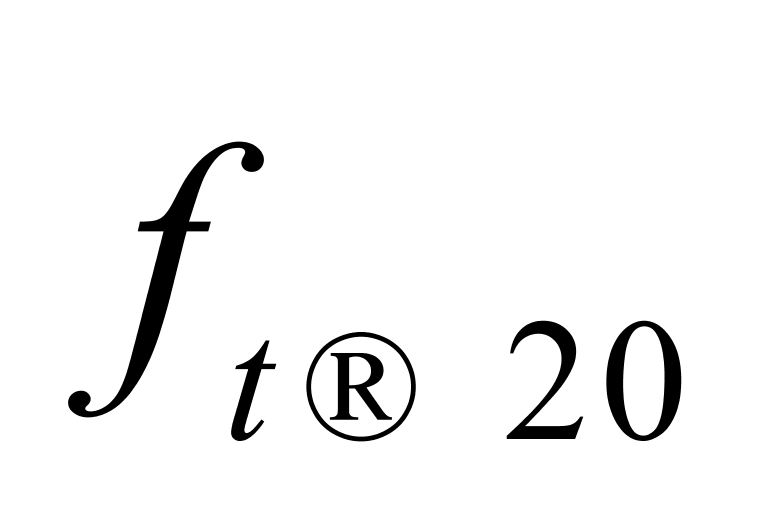 、
、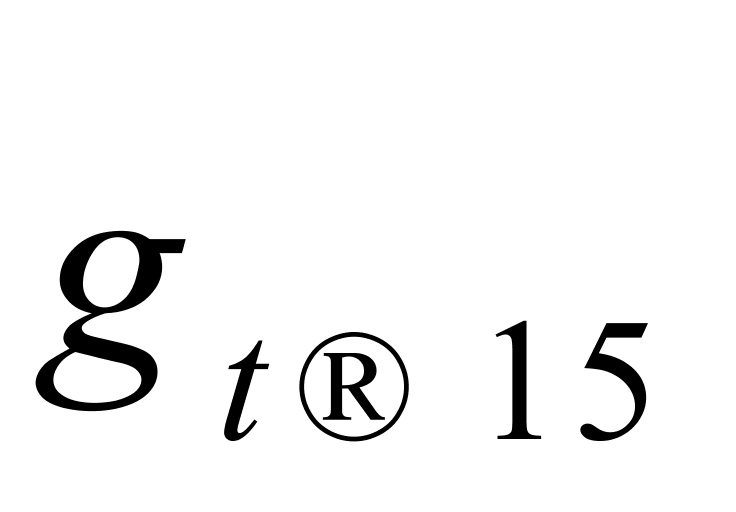 和
和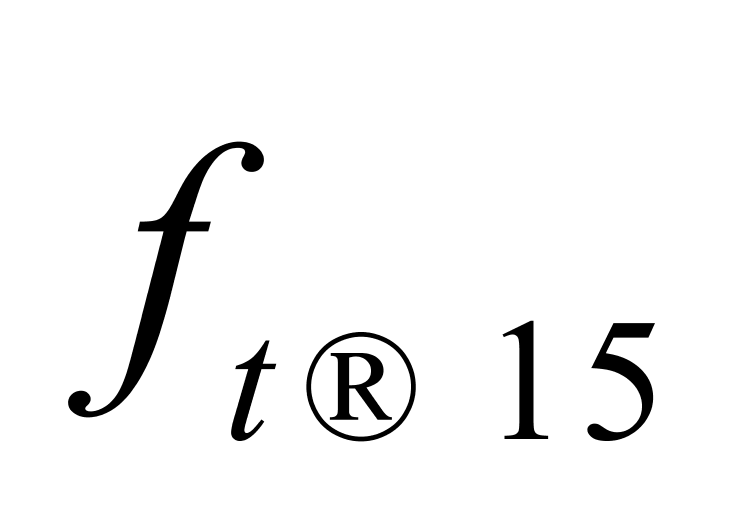 这4列数据的算术平均值及其修约后的结果,后者分别用符号
这4列数据的算术平均值及其修约后的结果,后者分别用符号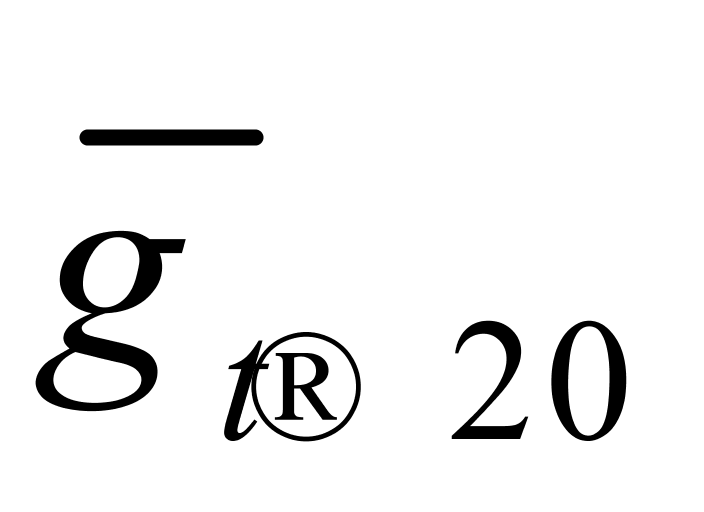 、
、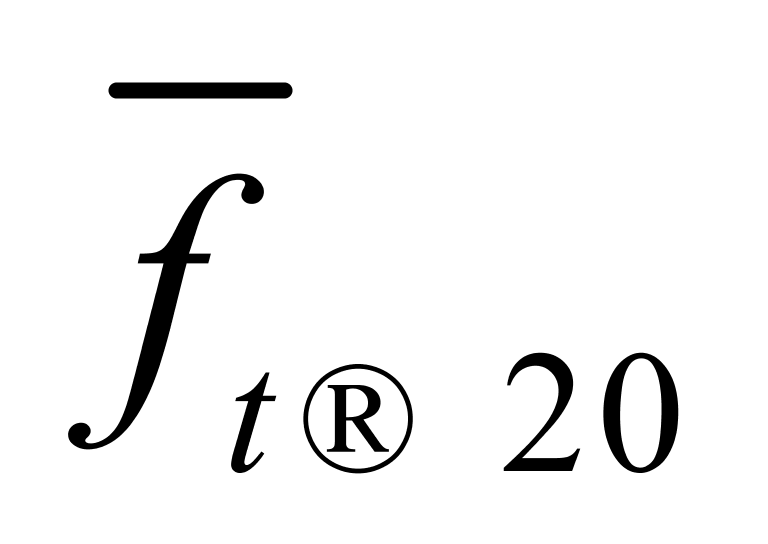 、
、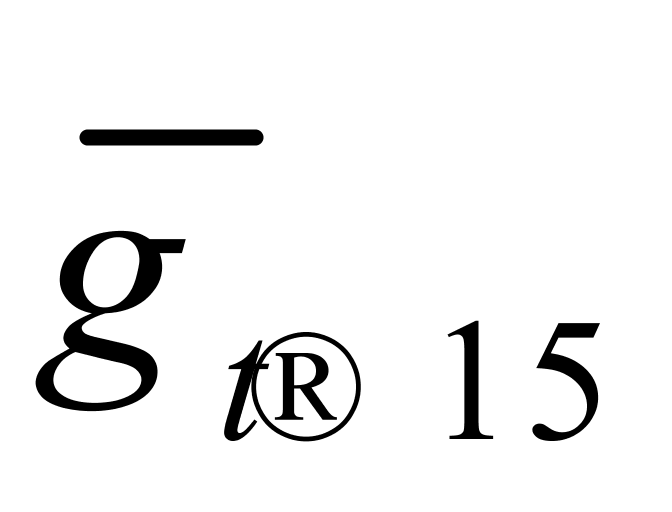 和
和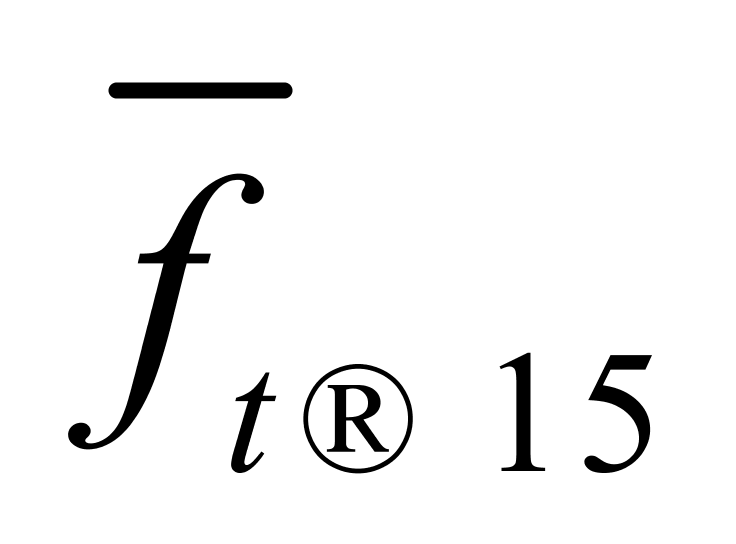 来表示。由于算术平均数与各数之差(即离差)的平方和最小,我们暂时把纯水在10~30℃温度区间内的密度温度系数和体积温度系数分别设定为
来表示。由于算术平均数与各数之差(即离差)的平方和最小,我们暂时把纯水在10~30℃温度区间内的密度温度系数和体积温度系数分别设定为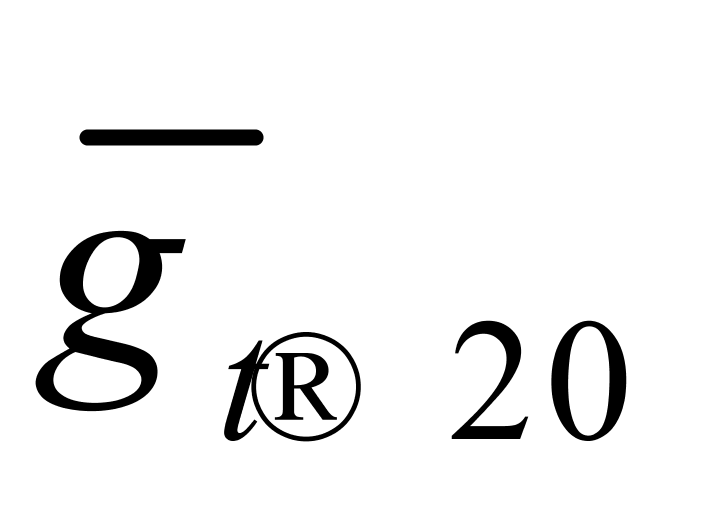 = 0.20 kg/(m3·℃)和
= 0.20 kg/(m3·℃)和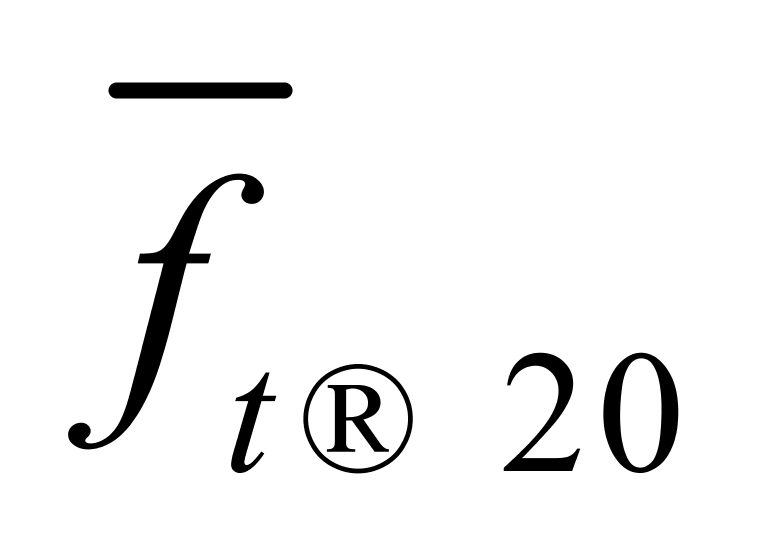 = 0.00020℃-1(暂不考虑
= 0.00020℃-1(暂不考虑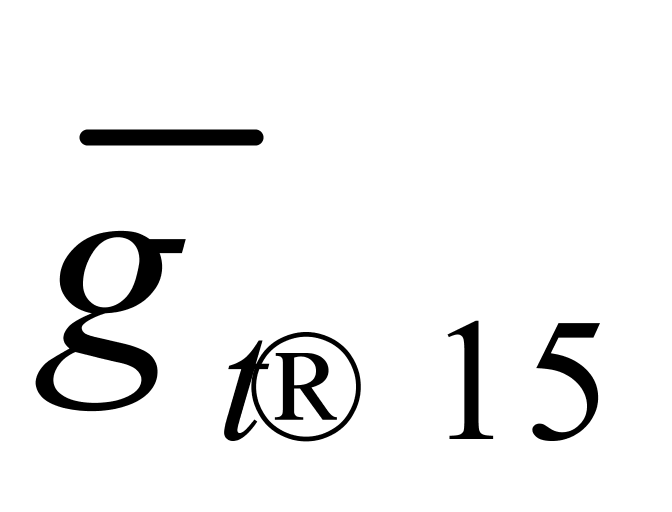 = 0.18 kg/(m3·℃)和
= 0.18 kg/(m3·℃)和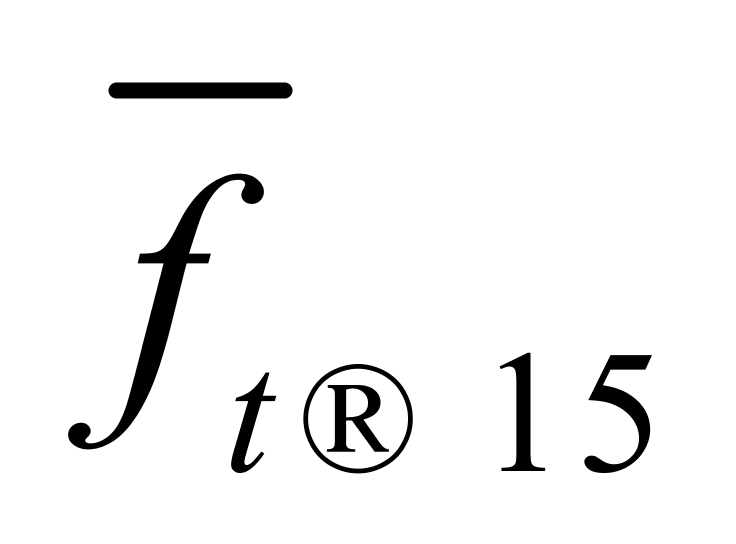 = 0.00018℃-1)。接下来,我们分析所取的这两个系数值对计算纯水重量所产生的误差。
= 0.00018℃-1)。接下来,我们分析所取的这两个系数值对计算纯水重量所产生的误差。
由(8)式可得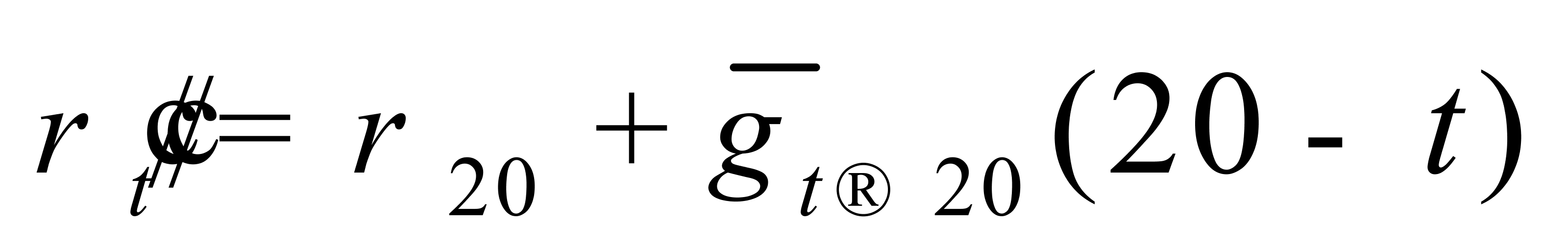 ,即
,即
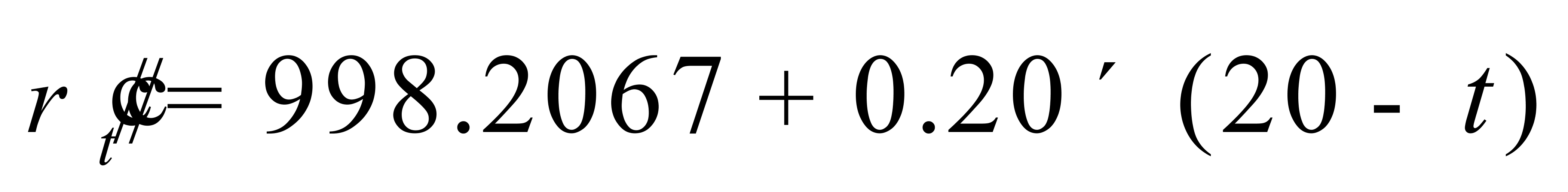 (11)
(11)
式中:
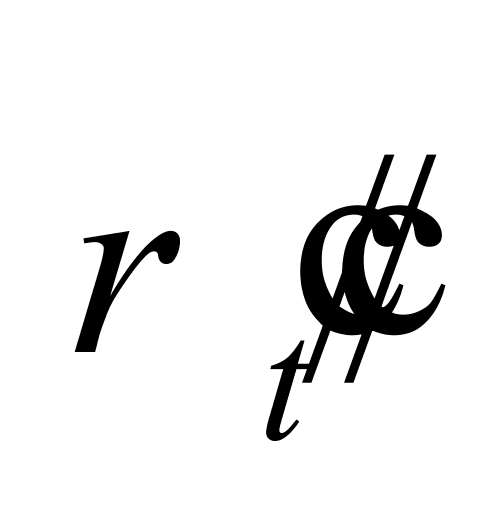 ——用
——用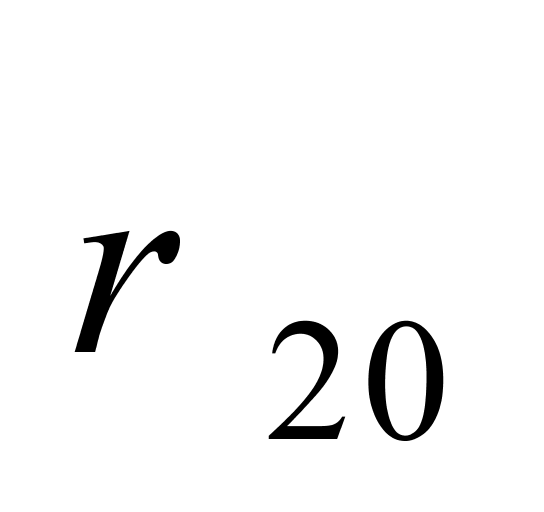 =998.2067 kg/m3及
=998.2067 kg/m3及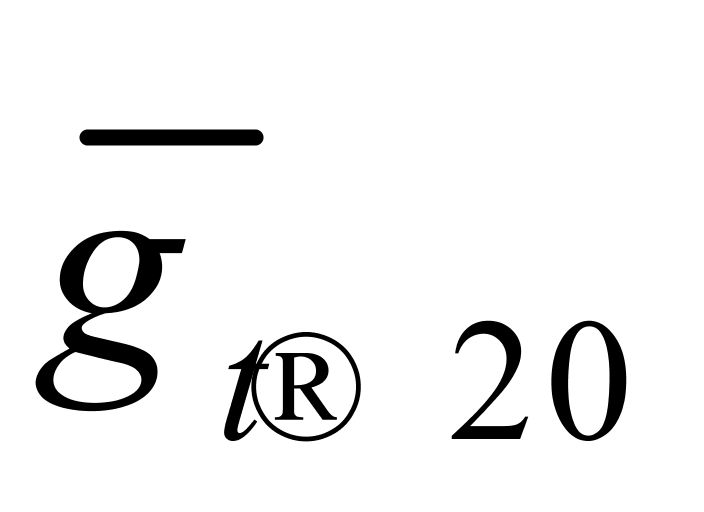 = 0.20 kg/(m3·℃)反推得到的纯水密度,kg/m3。
= 0.20 kg/(m3·℃)反推得到的纯水密度,kg/m3。
图2中的浅绿色线段即表示通过(11)式反推得到的纯水密度与温度的关系(具体数据见表1)。从图2中可以看出:一是总体上有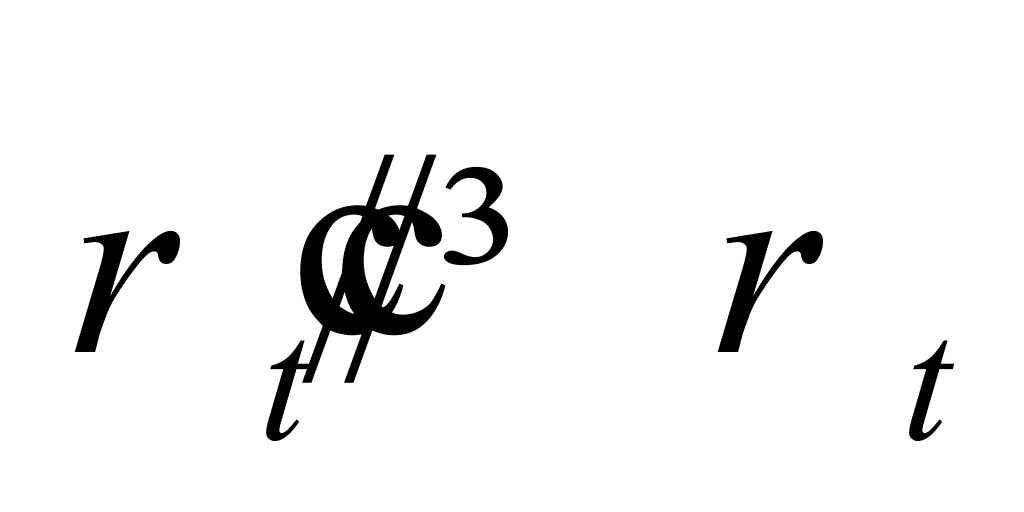 ,且
,且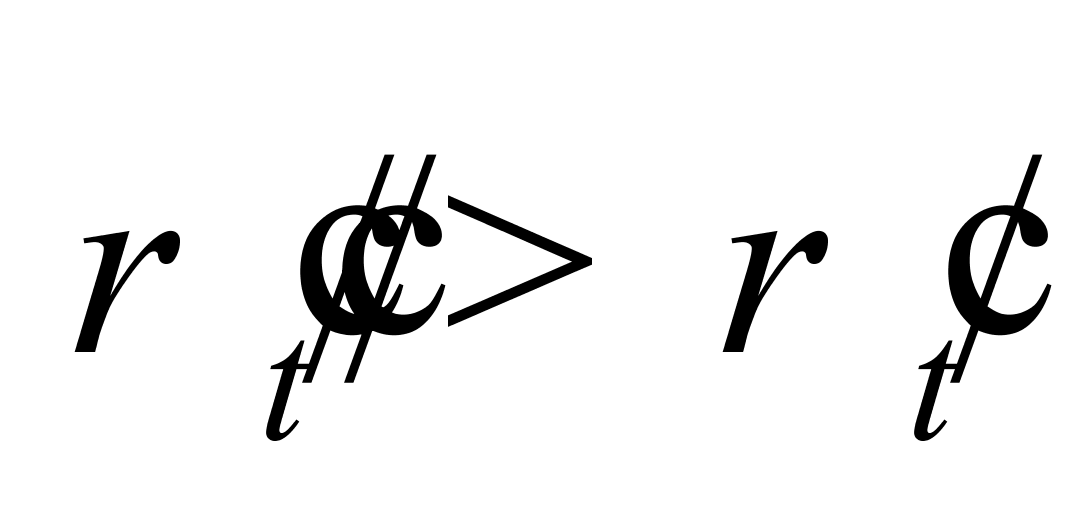 ;二是
;二是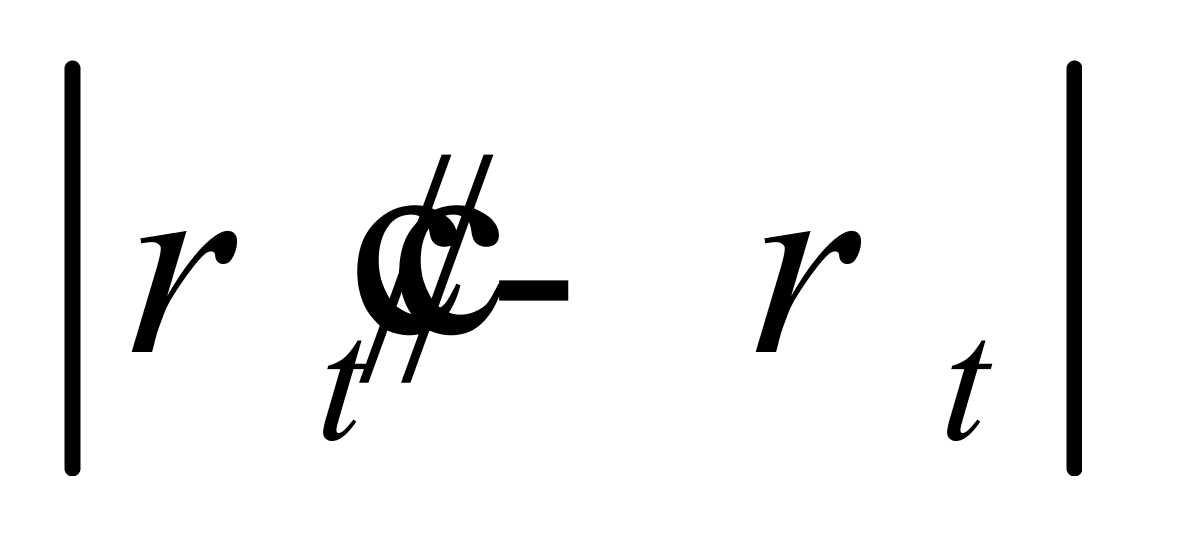 的极大值出现在温度区间的上下两限,温度越接近基准温度(20℃),
的极大值出现在温度区间的上下两限,温度越接近基准温度(20℃),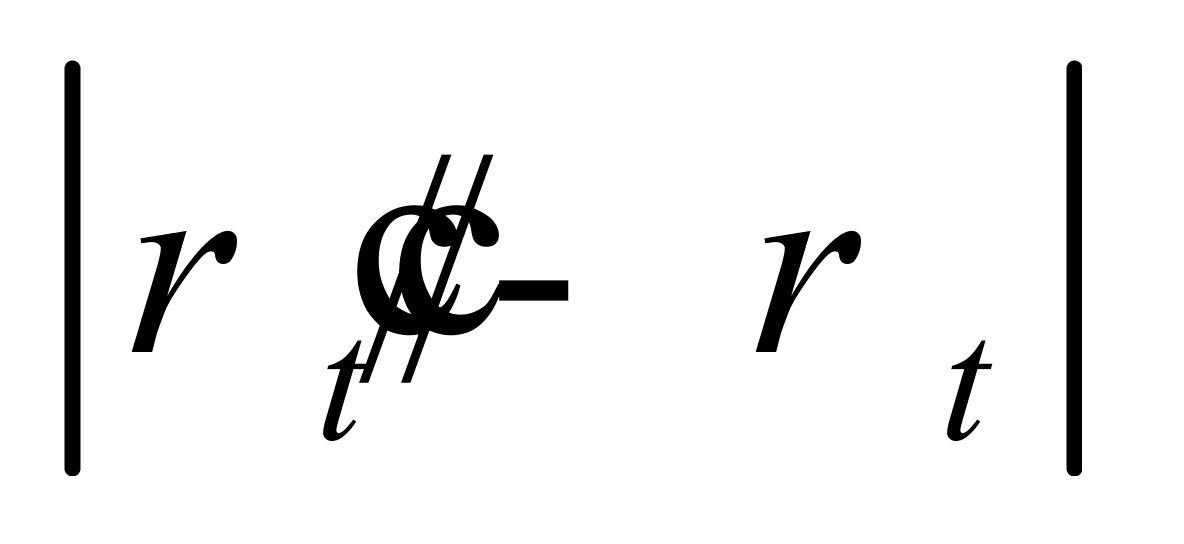 越小;三是
越小;三是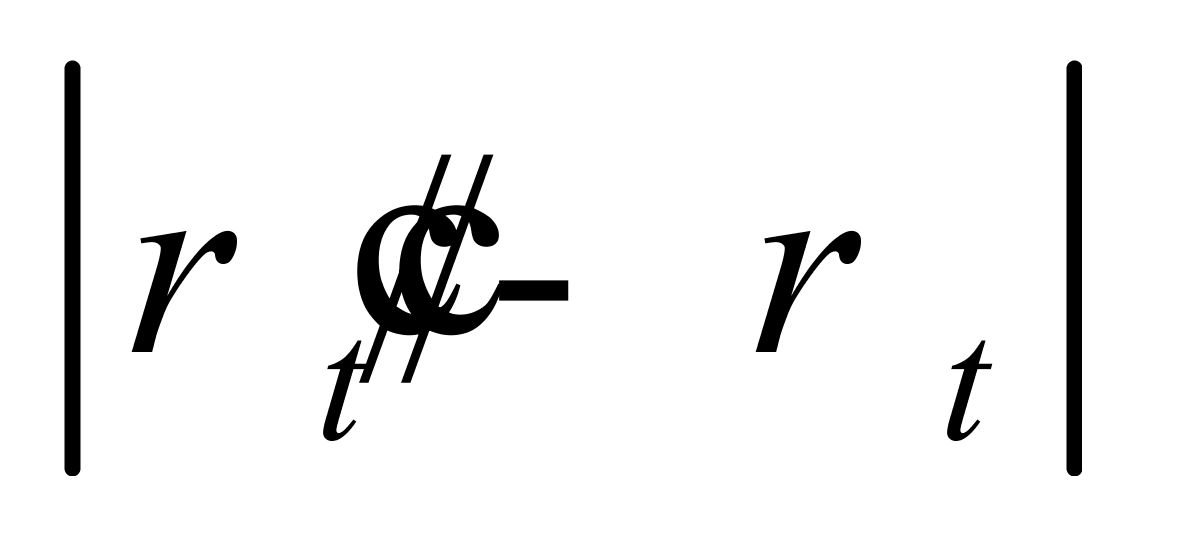 的极大值要远大于
的极大值要远大于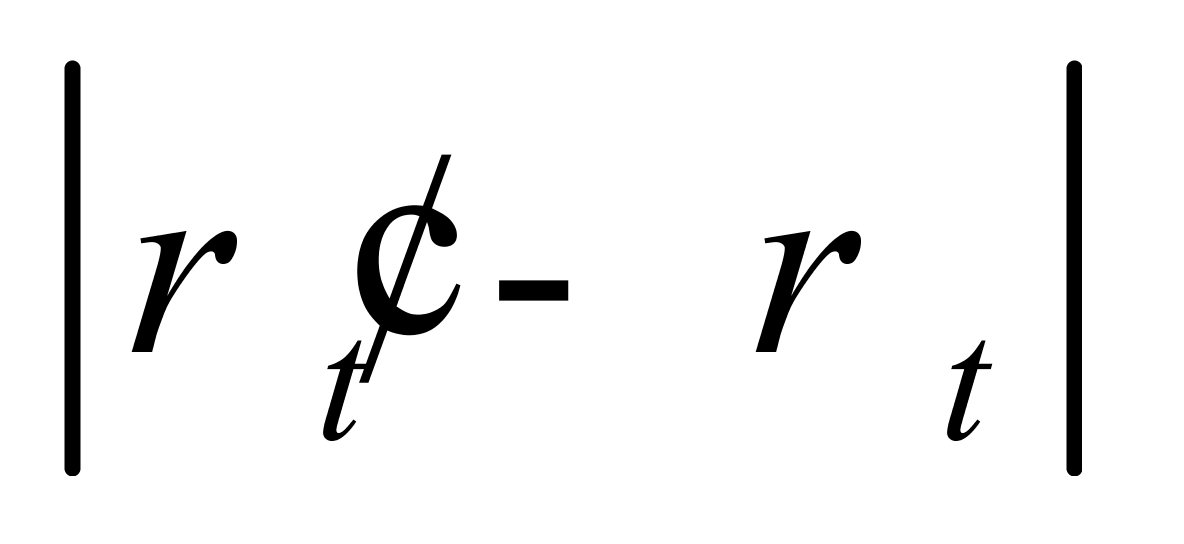 的极大值,但在基准温度(20 ℃)附近,
的极大值,但在基准温度(20 ℃)附近,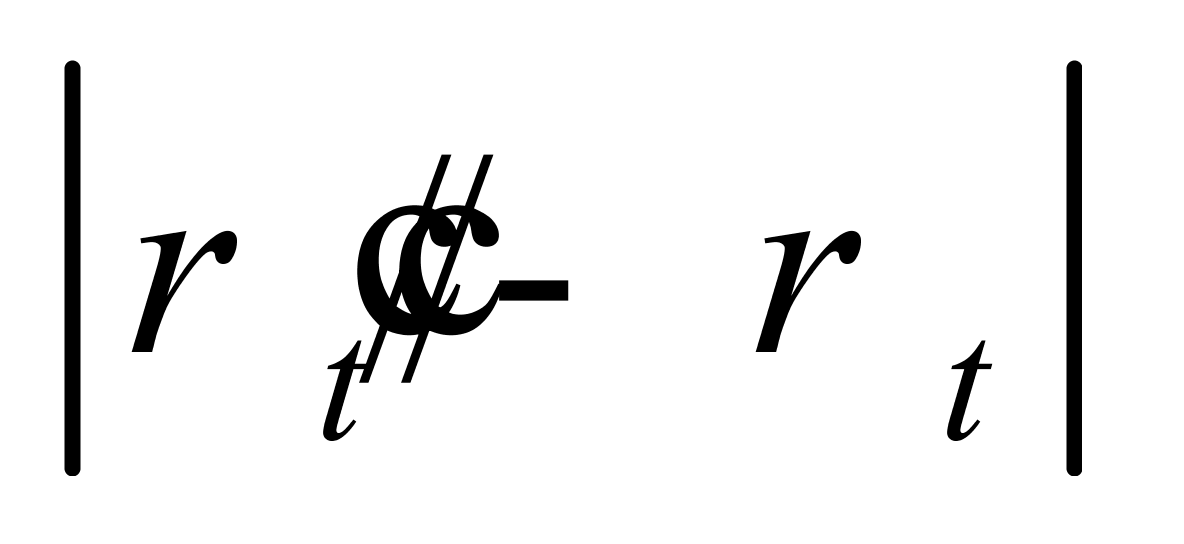 远小于
远小于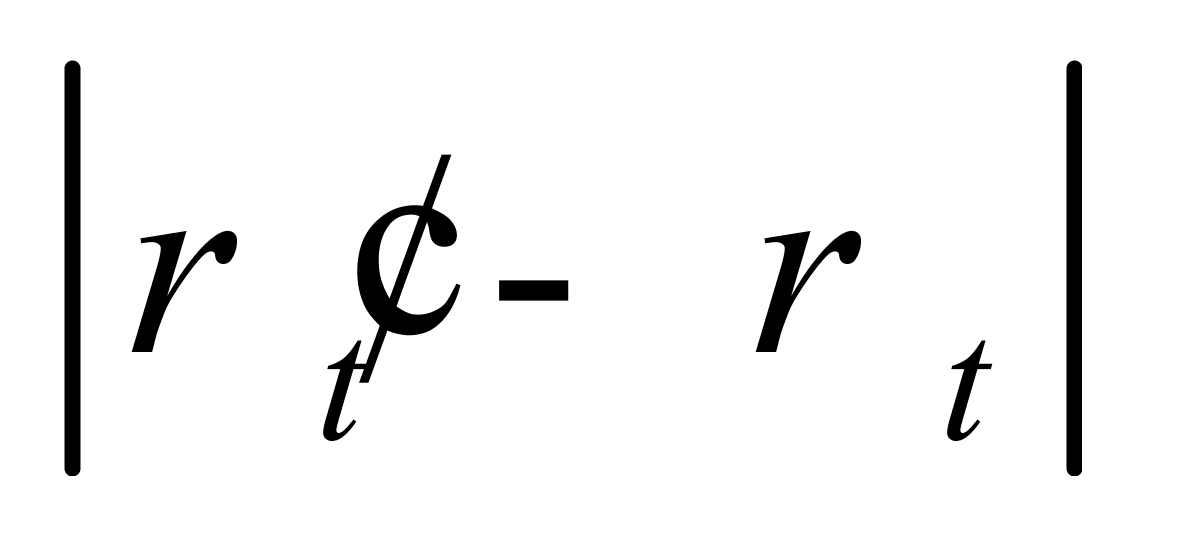 ;四是在纯水密度-温度直角坐标系中,浅绿色线段的斜率恰好是
;四是在纯水密度-温度直角坐标系中,浅绿色线段的斜率恰好是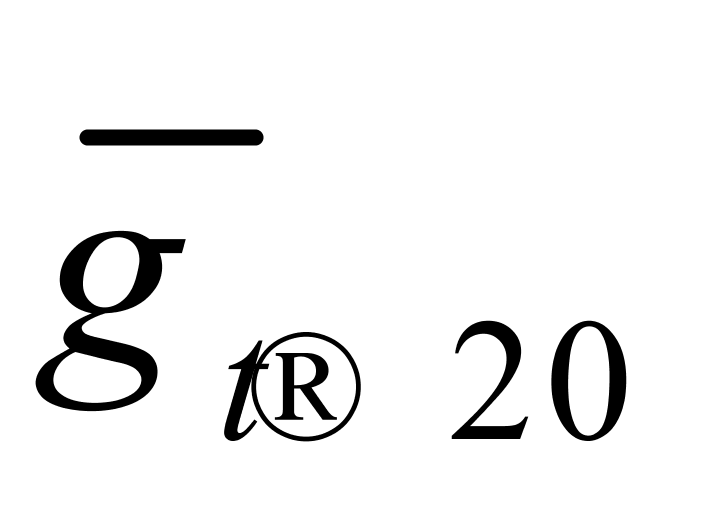 的相反数,即-0.20,而对(7)式中的系数进行相应修约后也是这个值③。
的相反数,即-0.20,而对(7)式中的系数进行相应修约后也是这个值③。
由(9)式可得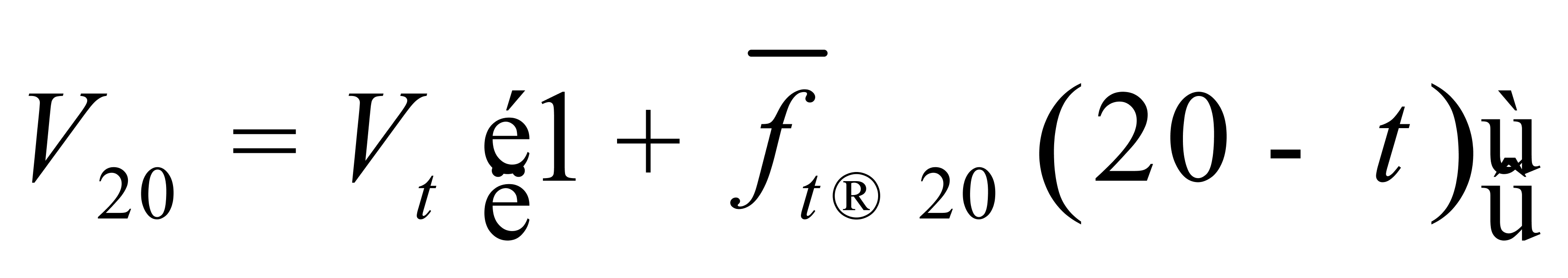 ,即
,即
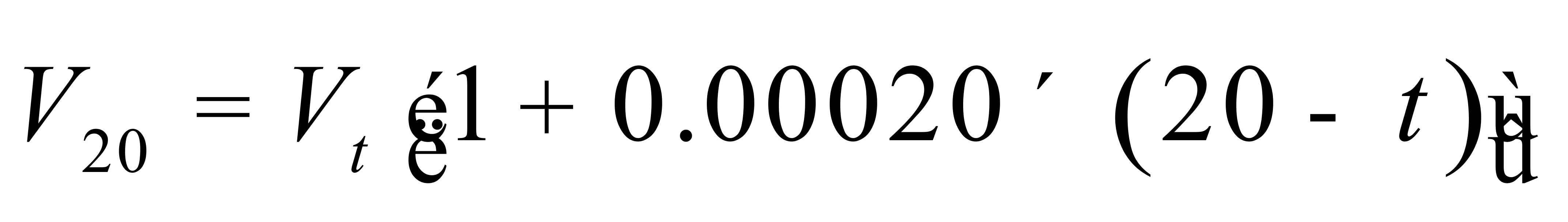 (12)
(12)
利用(11)式或(12)式计算纯水重量时,所产生的相对误差可用下列公式表示:
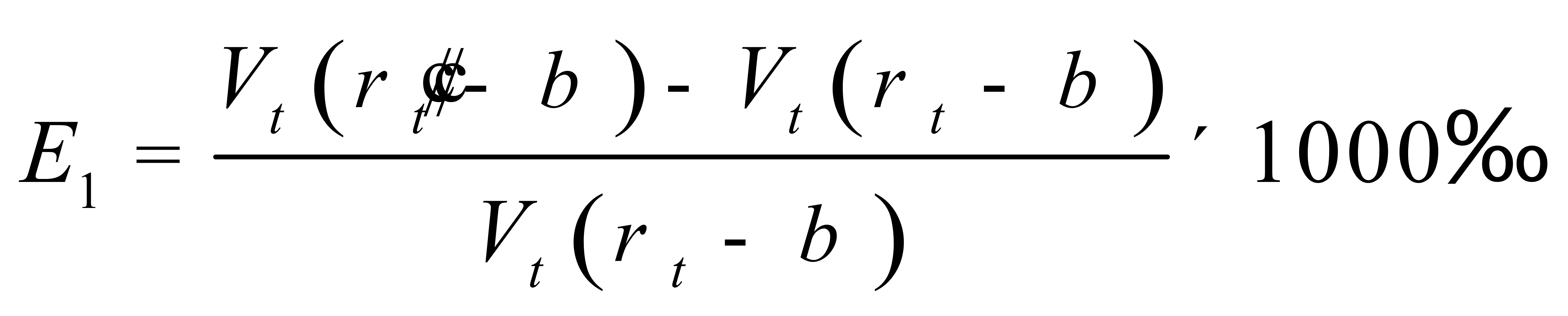
(13)
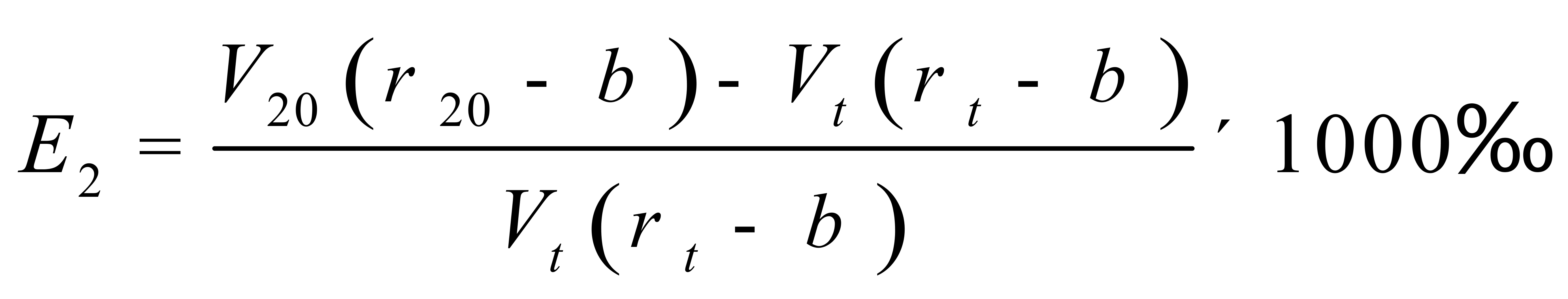
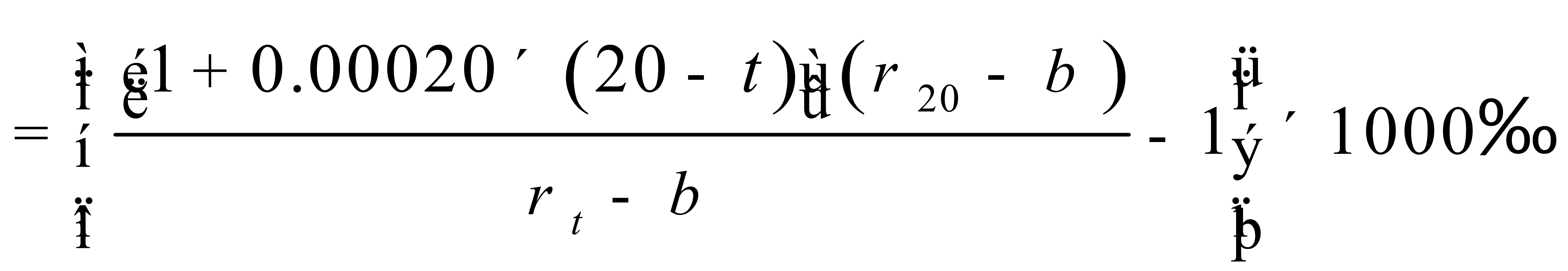 (14)
(14)
式中:
E1、E2——采用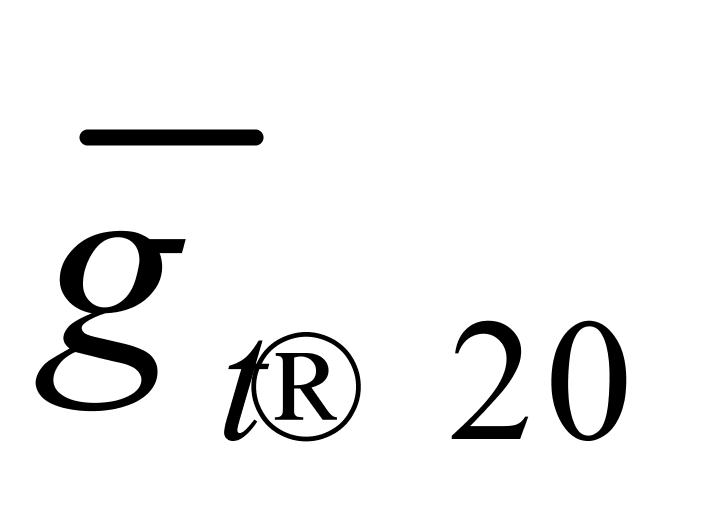 和
和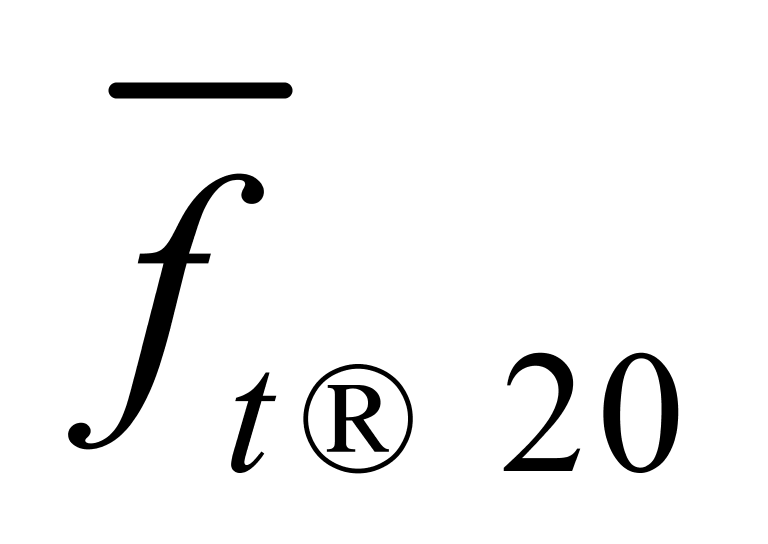 计算纯水重量时产生的相对误差,‰;
计算纯水重量时产生的相对误差,‰;
β——空气浮力修正值,kg/m3,这里取1.1 kg/m3。
表3按1℃的温度间隔列出了用上述确定的系数值计算纯水重量所产生的相对误差。从中可以看出:一是重量计算结果总体上呈正偏差;二是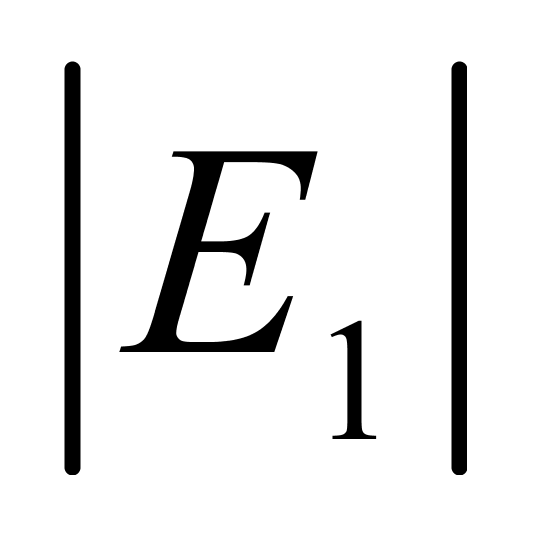 和
和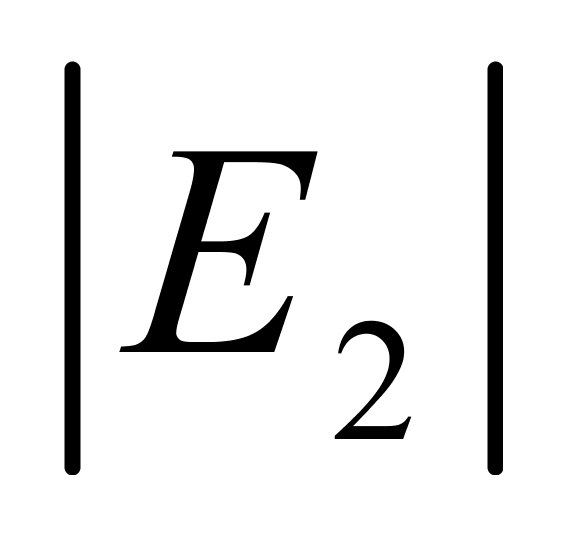 的极大值出现在温度区间的上下两限,温度越接近基准温度(20℃),它们的值越小;三是当t=30℃时,
的极大值出现在温度区间的上下两限,温度越接近基准温度(20℃),它们的值越小;三是当t=30℃时,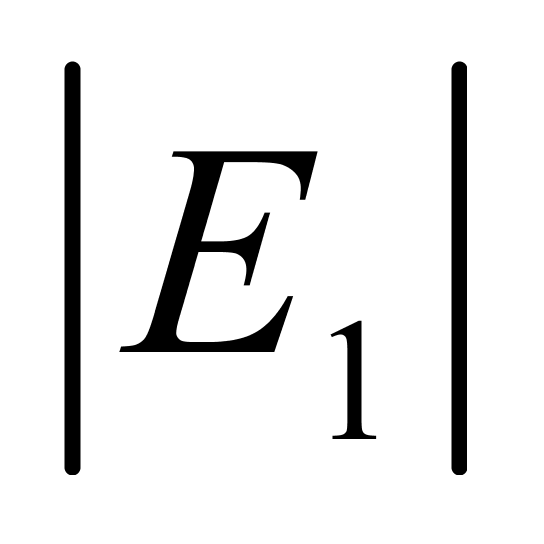 和
和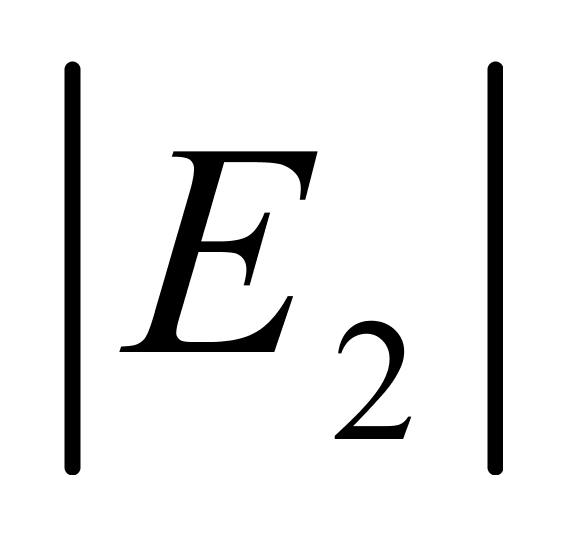 均达到最大值,约为0.57‰;四是当温度低于18℃时,
均达到最大值,约为0.57‰;四是当温度低于18℃时,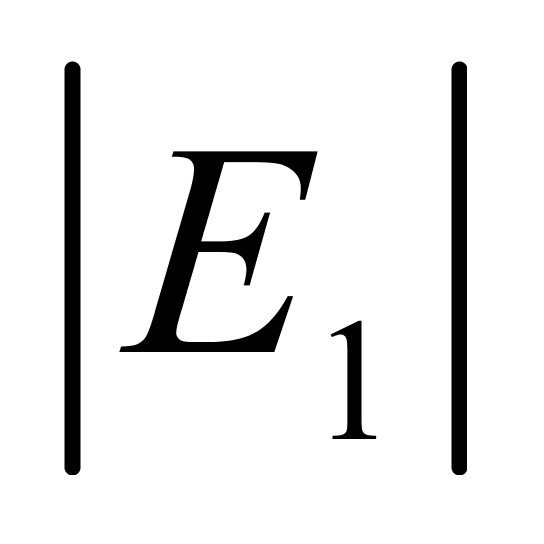 >
>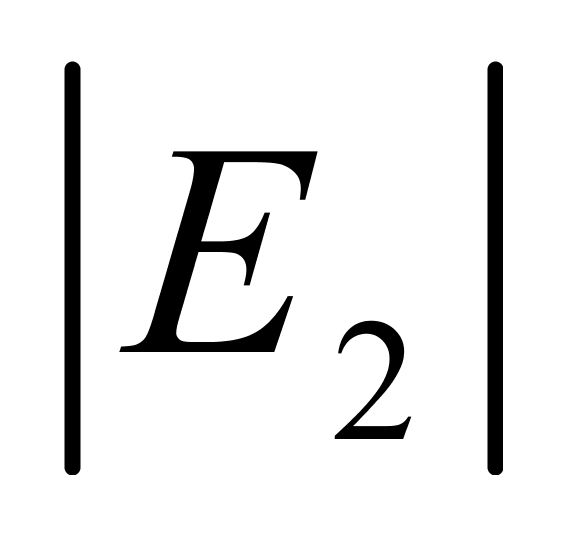 ,而当温度高于19℃时,
,而当温度高于19℃时,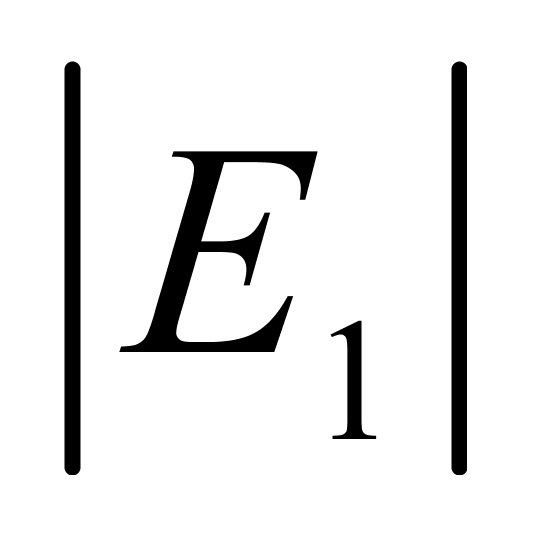 ≤
≤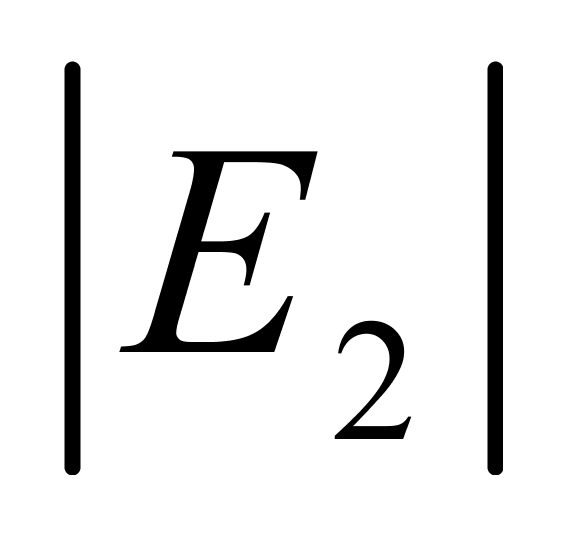 。除此,两种计算方法并没有明显的差异(或优劣)。由此可见,按上述方法所确定的纯水的这两个系数值是可以接受的。
。除此,两种计算方法并没有明显的差异(或优劣)。由此可见,按上述方法所确定的纯水的这两个系数值是可以接受的。
我们从表2和表3中可进一步看到:一是虽然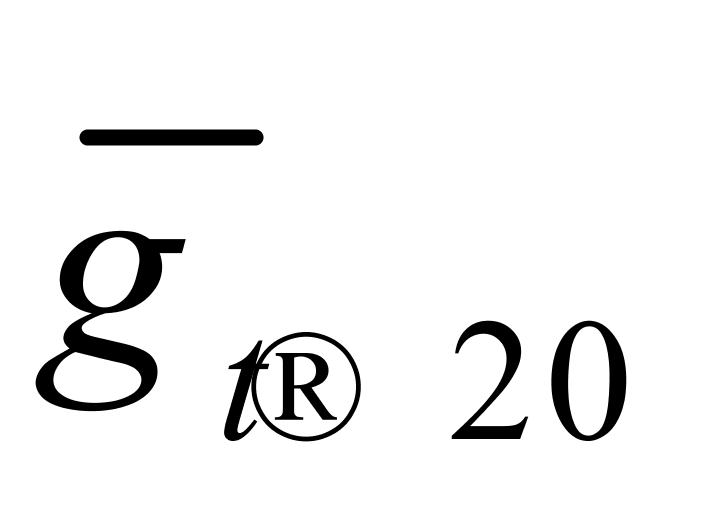 与
与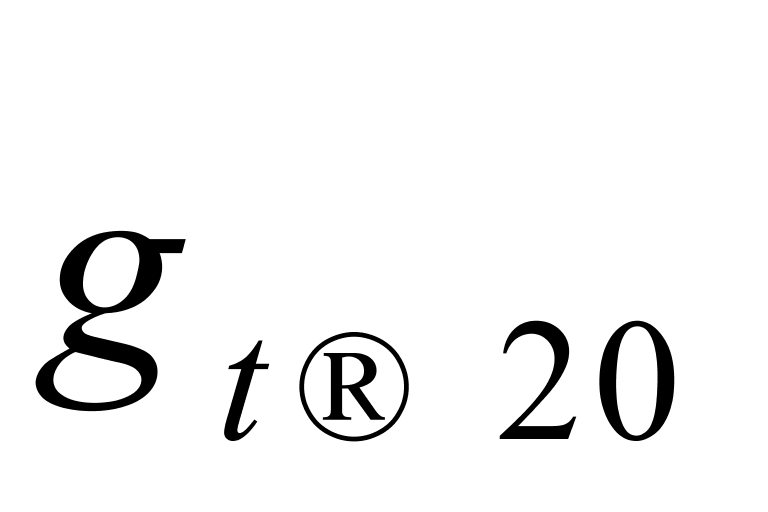 的最大值(即
的最大值(即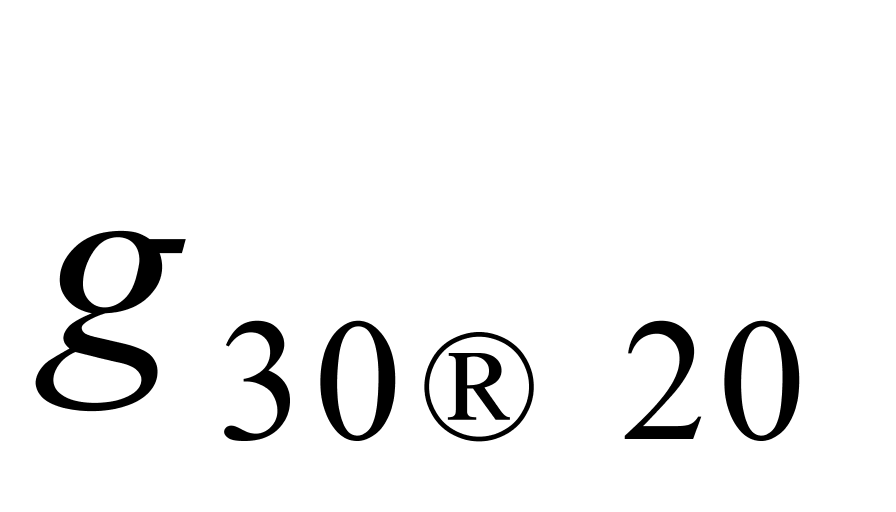 )和最小值(即
)和最小值(即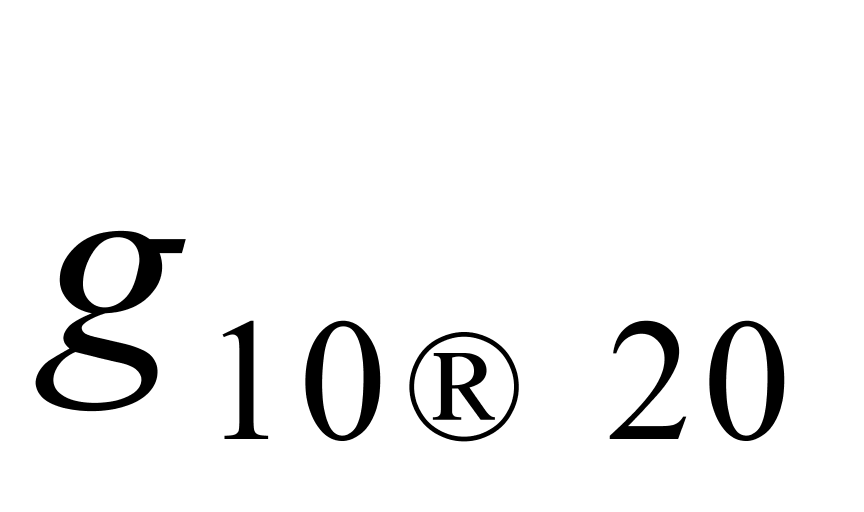 )均相差了大约0.05 kg/(m3·℃),
)均相差了大约0.05 kg/(m3·℃),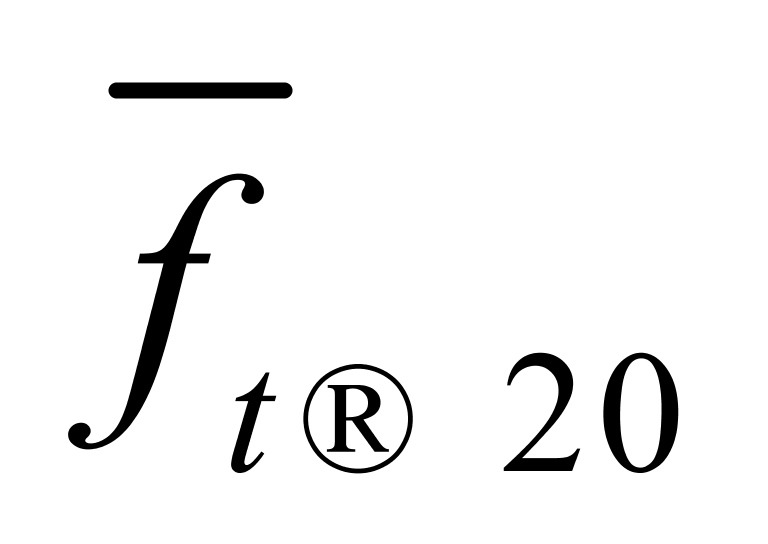 与
与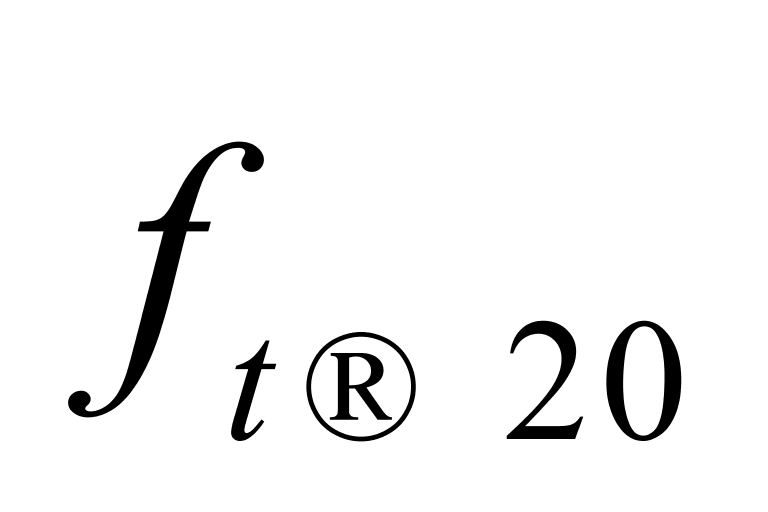 的最大值(即
的最大值(即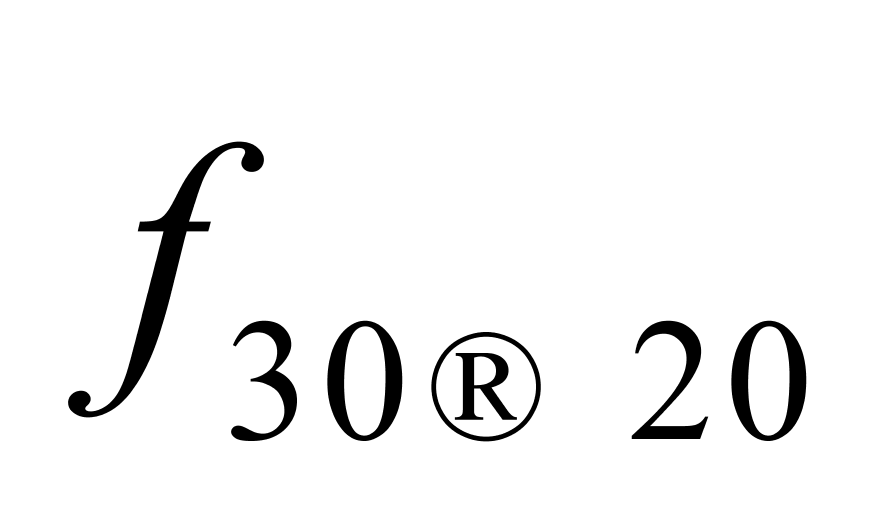 )和最小值(即
)和最小值(即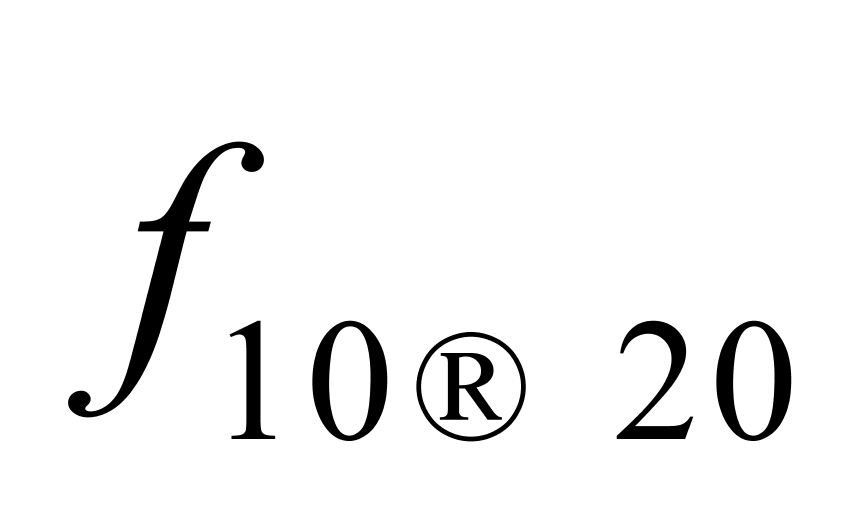 )也都相差了大约0.00005 ℃-1,但用这两个均值来计算纯水重量所产生的相对误差的最大值约为0.57‰(应该不算大);二是如果在计算纯水重量时将
)也都相差了大约0.00005 ℃-1,但用这两个均值来计算纯水重量所产生的相对误差的最大值约为0.57‰(应该不算大);二是如果在计算纯水重量时将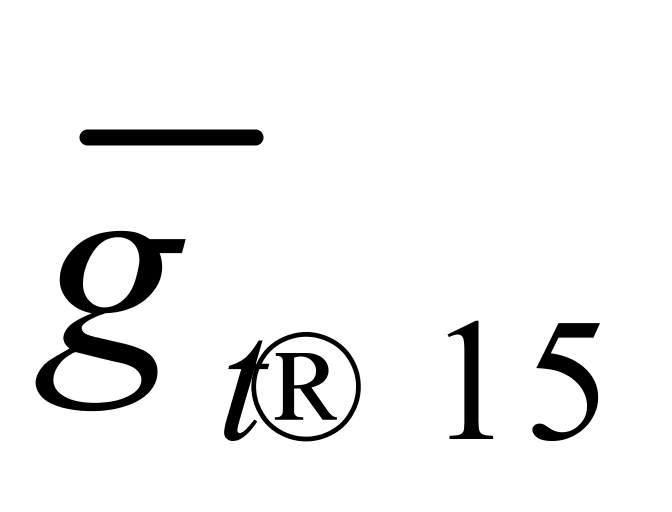 当作
当作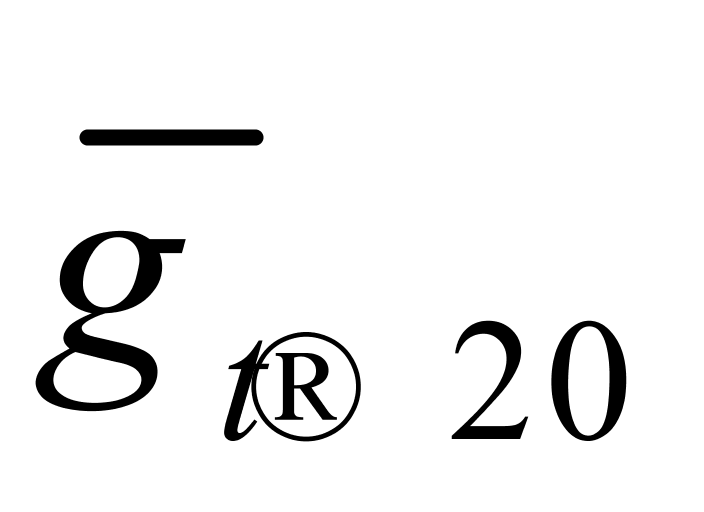 使用,
使用,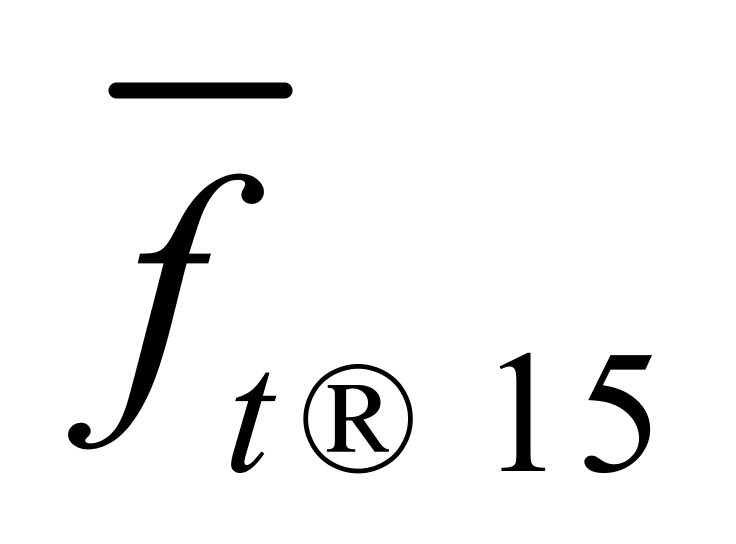 当作
当作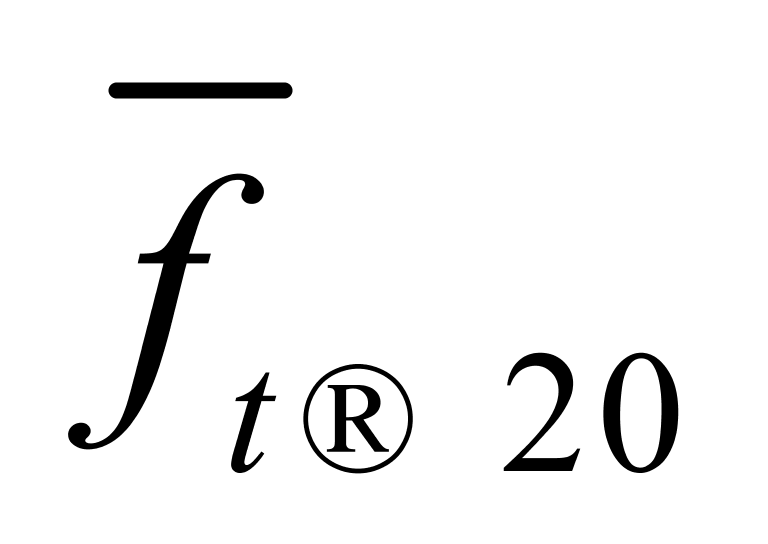 使用,所产生的相对误差的绝对值在纯水温度不高于基准温度(20℃)时反而较小,而在纯水温度不高于28℃时,也不会超过0.54‰。因此,在10℃~30℃范围内借用日本海事鉴定协会与新日本检定协会发布的化工品系数表④进行重量计算是可以接受的。
使用,所产生的相对误差的绝对值在纯水温度不高于基准温度(20℃)时反而较小,而在纯水温度不高于28℃时,也不会超过0.54‰。因此,在10℃~30℃范围内借用日本海事鉴定协会与新日本检定协会发布的化工品系数表④进行重量计算是可以接受的。
表3 用确定的相关系数值计算纯水重量所产生的相对误差
Table 3 Relative error in calculating water weight caused by the determined factors
℃ | kg/m3 | ‰ | ‰ | ‰ | ‰ |
10.0 | 999.7027 | 0.5047 | 0.4989 | 0.3044 | 0.2992 |
11.0 | 999.6081 | 0.3992 | 0.3940 | 0.2189 | 0.2142 |
12.0 | 999.5005 | 0.3067 | 0.3021 | 0.1464 | 0.1423 |
13.0 | 999.3801 | 0.2270 | 0.2229 | 0.0867 | 0.0831 |
14.0 | 999.2474 | 0.1596 | 0.1561 | 0.0394 | 0.0362 |
15.0 | 999.1026 | 0.1043 | 0.1014 | 0.0041 | 0.0015 |
16.0 | 998.9459 | 0.0609 | 0.0586 | -0.0192 | -0.0213 |
17.0 | 998.7778 | 0.0290 | 0.0272 | -0.0312 | -0.0327 |
18.0 | 998.5984 | 0.0083 | 0.0072 | -0.0318 | -0.0328 |
19.0 | 998.4079 | -0.0012 | -0.0018 | -0.0213 | -0.0218 |
20.0 | 998.2067 | 0.0000 | 0.0000 | 0.0000 | 0.0000 |
21.0 | 997.9950 | 0.0117 | 0.0123 | 0.0318 | 0.0323 |
22.0 | 997.7730 | 0.0338 | 0.0350 | 0.0739 | 0.0750 |
23.0 | 997.5408 | 0.0661 | 0.0679 | 0.1263 | 0.1279 |
24.0 | 997.2988 | 0.1083 | 0.1106 | 0.1886 | 0.1907 |
25.0 | 997.0470 | 0.1603 | 0.1633 | 0.2608 | 0.2634 |
26.0 | 996.7857 | 0.2220 | 0.2254 | 0.3425 | 0.3456 |
27.0 | 996.5151 | 0.2929 | 0.2970 | 0.4336 | 0.4373 |
28.0 | 996.2353 | 0.3732 | 0.3779 | 0.5340 | 0.5382 |
29.0 | 995.9465 | 0.4626 | 0.4678 | 0.6435 | 0.6482 |
30.0 | 995.6488 | 0.5610 | 0.5668 | 0.7621 | 0.7673 |
我们还可按不同温度间隔来计算纯水的密度温度系数均值和体积温度系数均值,但所得到的结果并没有明显的差异(见表4)。
表4 不同温度间隔下纯水的密度温度系数均值和体积温度系数均值
Table 4 The mean of the density temperature factor and volume temperature factor of water at different temperature intervals
℃ | kg/(m3·℃) | ℃-1 | kg/(m3·℃) | ℃-1 |
0.1 | 0.21 | 0.00021 | 0.18 | 0.00018 |
1 | 0.20 | |||
5 | 0.00020 | |||
10 | / | / | ||
10-15-30 | / | / | 0.18 | 0.00018 |
因此,对于温度区间在10℃~30℃的纯水,取5℃的温度间隔来确定其系数值是足够的,这将大幅减小测定密度的工作量。
至此可以看出,液态物质的密度温度系数和体积温度系数虽然是根据各自的定义式来确定的,但并不等同于由各自定义式直接计算得到的值,而是在一定温度范围内多个温度间隔点的计算值的算术平均值。
顺便指出,如果将(5)式改为
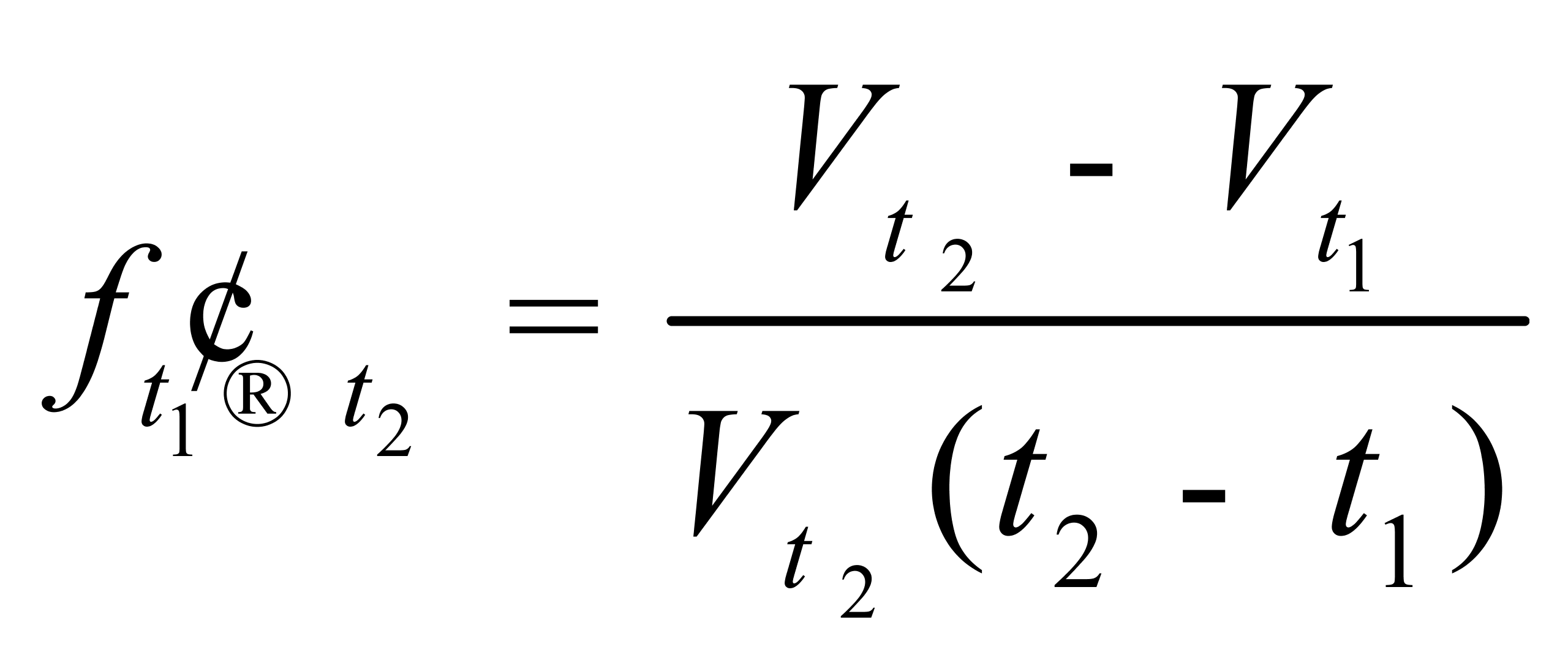 (15)
(15)
或
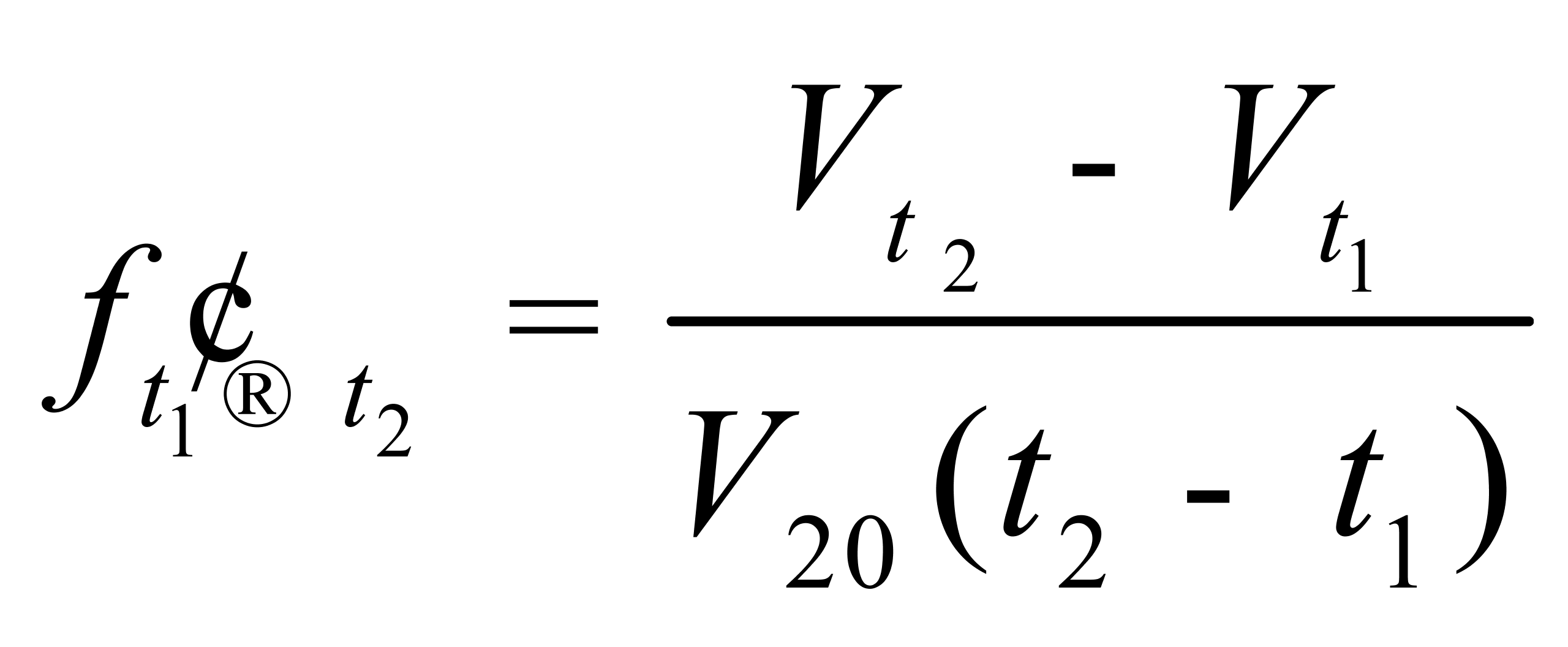 (16)
(16)
则均有
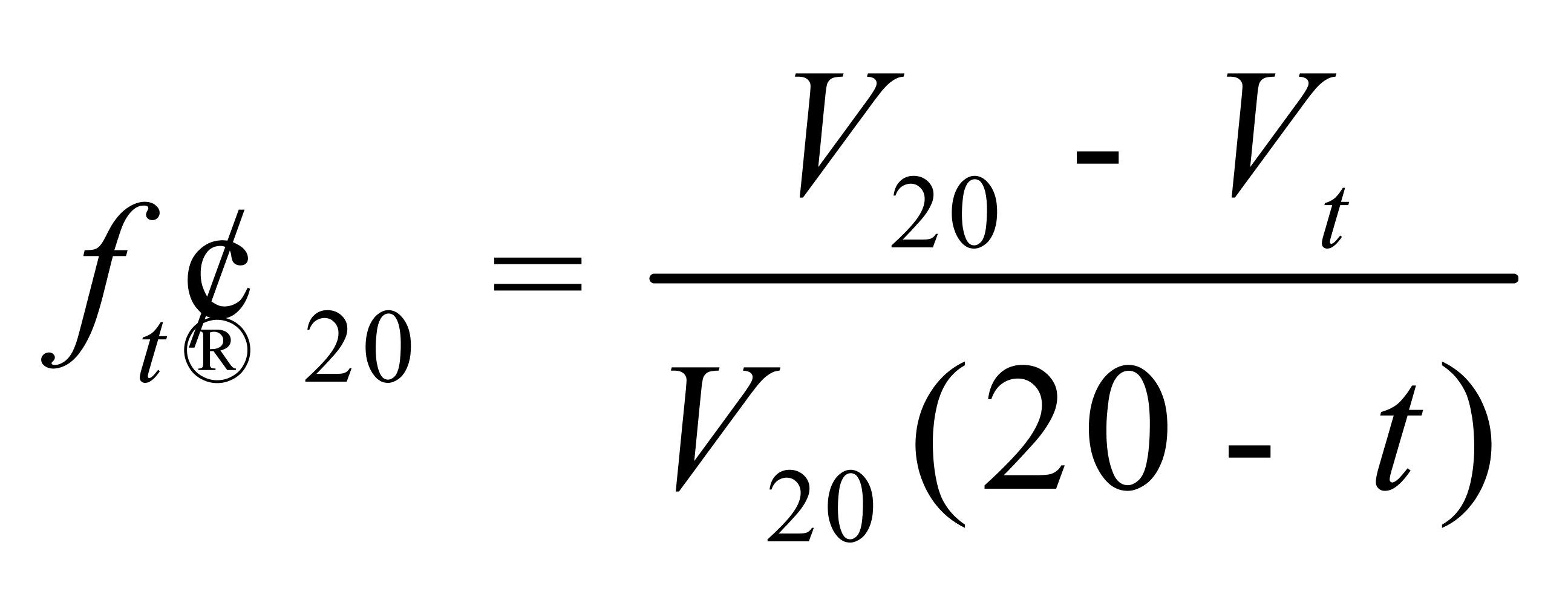 (17)
(17)
虽然,根据(17)式并沿用上述方法仍可确定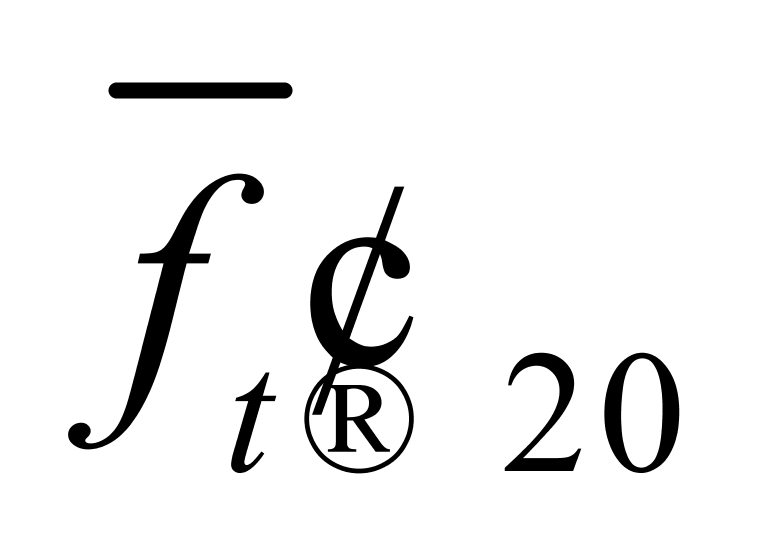 为0.00021℃-1或0.00020℃-1,但若用这两个值并采用(17)式来计算纯水的重量,其相对误差的绝对值要比表3第4列中的绝对值大很多⑤。因此,(5)式才是相对合理的。
为0.00021℃-1或0.00020℃-1,但若用这两个值并采用(17)式来计算纯水的重量,其相对误差的绝对值要比表3第4列中的绝对值大很多⑤。因此,(5)式才是相对合理的。
2 精炼棕榈油密度温度系数的探讨
2002年,刘一军等探讨了精炼棕榈油(包括精炼棕榈软脂、精炼棕榈油和精炼棕榈硬脂,下同)密度和温度的线性关系[10];2015年,刘新等又探讨了精炼棕榈液油(本文称之为精炼棕榈软脂)的密度温度系数对计重的影响[7]。两者分别给出了精炼棕榈油和精炼棕榈软脂在不同温度下的实测密度,这为我们按前述方法确定精炼棕榈油的密度温度系数提供了可能。最终确定的精炼棕榈油密度温度系数见表5,详细的确定过程见表6,误差分析见表7⑥。
表5 精炼棕榈油密度温度系数
Table 5 The density temperature factor of RBD palm oil
品种 | ℃ | kg/(m3·℃) | 线性回归方程中温度t的系数的绝对值 |
(熔点不大于24℃) | 30 | 0.68 | 0.68 |
精炼棕榈油⑦ | 35 | 0.68 | 0.67 |
精炼棕榈硬脂 | 60 | 0.67 | 0.67 |
表6 精炼棕榈油密度温度系数计算表
Table 6 Work sheet for the density temperature factor of RBD palm oil
品种 | ℃ | kg/m3 | kg/(m3·℃) | 品种 | ℃ | kg/m3 | kg/(m3·℃) | 品种 | ℃ | kg/m3 | kg/(m3·℃) |
(熔点不大于24 ℃) | 30 | 905.0 | / | 精炼棕榈油 | 35 | 901.1 | / | 精炼棕榈硬脂 | 55 | 886.1 | 0.660000 |
35 | 901.6 | 0.680000 | 40 | 897.6 | 0.700000 | 60 | 882.8 | / | |||
40 | 898.2 | 0.680000 | 45 | 894.2 | 0.690000 | 65 | 879.4 | 0.680000 | |||
45 | 894.8 | 0.680000 | 50 | 890.8 | 0.686667 | 70 | 876.1 | 0.670000 | |||
50 | 891.4 | 0.680000 | 55 | 887.5 | 0.680000 | 75 | 872.7 | 0.673333 | |||
55 | 888.0 | 0.680000 | 60 | 884.2 | 0.676000 | / | / | / | |||
60 | 884.7 | 0.676667 | 65 | 880.8 | 0.676667 | / | / | / |
表7 用表5确定的密度温度系数反推纯水密度所产生的误差
Table 7 Density error of water caused by the density temperature factor determined in Table 5
品种 | ℃ | kg/m3 | kg/m3 | kg/m3 | 品种 | ℃ | kg/m3 | kg/m3 | kg/m3 |
精炼棕榈软脂(熔点不大于 24 ℃) | 30 | 905.0 | 905.0 | 0.0 | 精炼棕榈软脂(熔点20.9 ℃) | 30 | 904.9 | 904.9 | 0.0 |
31 | 904.3 | 904.3 | 0.0 | 31 | 904.3 | 904.2 | -0.1 | ||
35 | 901.6 | 901.6 | 0.0 | 32 | 903.6 | 903.5 | -0.1 | ||
37 | 900.2 | 900.2 | 0.0 | 33 | 902.9 | 902.9 | 0.0 | ||
40 | 898.2 | 898.2 | 0.0 | 34 | 902.2 | 902.2 | 0.0 | ||
42 | 896.8 | 896.8 | 0.0 | 35 | 901.5 | 901.5 | 0.0 | ||
45 | 894.8 | 894.8 | 0.0 | 36 | 900.9 | 900.8 | -0.1 | ||
49 | 892.1 | 892.1 | 0.0 | 37 | 900.2 | 900.1 | -0.1 | ||
50 | 891.4 | 891.4 | 0.0 | 38 | 899.5 | 899.5 | 0.0 | ||
53 | 889.4 | 889.4 | 0.0 | 39 | 898.8 | 898.8 | 0.0 | ||
55 | 888.0 | 888.0 | 0.0 | 40 | 898.1 | 898.1 | 0.0 | ||
58 | 886.0 | 886.0 | 0.0 | 41 | 897.4 | 897.4 | 0.0 | ||
60 | 884.6 | 884.6 | 0.0 | 42 | 896.8 | 896.7 | -0.1 | ||
精炼棕榈油 | 35 | 901.1 | 901.1 | 0.0 | 43 | 896.1 | 896.1 | 0.0 | |
36 | 900.4 | 900.4 | 0.0 | 44 | 895.4 | 895.4 | 0.0 | ||
40 | 897.6 | 897.7 | 0.1 | 45 | 894.7 | 894.7 | 0.0 | ||
41 | 897.0 | 897.0 | 0.0 | 精炼棕榈硬脂 | 55 | 886.1 | 886.2 | 0.0 | |
45 | 894.2 | 894.3 | 0.1 | 58 | 884.1 | 884.1 | 0.0 | ||
47 | 892.8 | 892.9 | 0.1 | 60 | 882.8 | 882.8 | 0.0 | ||
50 | 890.8 | 890.9 | 0.1 | 63 | 880.8 | 880.8 | 0.0 | ||
53 | 888.8 | 888.9 | 0.1 | 65 | 879.4 | 879.5 | 0.0 | ||
55 | 887.5 | 887.5 | 0.0 | 68 | 877.4 | 877.4 | 0.0 | ||
60 | 884.3 | 884.1 | -0.2 | 70 | 876.1 | 876.1 | 0.0 | ||
65 | 880.8 | 880.7 | -0.1 | 71 | 875.4 | 875.4 | 0.0 | ||
66 | 880.1 | 880.0 | -0.1 | 73 | 874.2 | 874.1 | -0.1 | ||
70 | 877.5 | 877.3 | -0.2 | 75 | 872.7 | 872.8 | 0.0 |
从表7可以看出,把精炼棕榈软脂、精炼棕榈油和精炼棕榈硬脂的密度温度系数分别确定为0.68 kg/(m3·℃)、0.68 kg/(m3·℃)和0.67 kg/(m3·℃)是合理的。比较而言,如果将0.64 kg/(m3·℃)作为精炼棕榈油的密度温度系数,并用之进行重量计算,所产生的误差则要比表7中所列的大很多⑧。因此,刘新等“以加权平均温度密度为基准温度密度计算货物质量能最大程度减少误差”的建议[7]固然可取,但确定合理的密度温度系数似乎才是问题的关键所在。
3 结论
在基准温度上和/或下按5 ℃的温度间隔测定液态物质的密度,再分别按(8)式和(10)式计算各个温度间隔点对应的系数值,最后取它们的算术平均值作为液态物质相应的系数是可行的;据此将精炼棕榈软脂、精炼棕榈油和精炼棕榈硬脂的密度温度系数分别确定为0.68 kg/(m3·℃)、0.68 kg/(m3·℃)和0.67 kg/(m3·℃)是合理的。此外,在10℃~30℃范围内借用日本海事鉴定协会与新日本检定协会发布的化工品系数表进行重量计算亦是可以接受的。
【该文经 CNKI 学术不端文献检测系统检测,总文字复制比为0.2%。】
参考文献
[1] 石油 石油产品 化工品 动植物油容量计重[K]. 中华人民共和国辽宁进出口商品检验局. 1986: 190-213.
[2] 进出口商品鉴定业务编写组, 进出口商品重量鉴定学[M]. 北京: 电子工业出版社, 1991: 223.
[3] 张鹤卿, 沈运泉. 商检鉴定业务基础知识[Z]. 国家商检局人教司教育处, 1997: 214-216.
[4] 国家质量监督检验检疫总局检验监管司. 进出口商品检验鉴定人员培训教材(下册)进出口商品检验鉴定实务[M]. 北京: 中国标准出版社, 2004: 177-179.
[5] SN/T 2389.11-2012 进出口商品容器计重规程 第11部分:液体化工品岸上立式金属罐静态计重[S].
[6] SN/T 2389.2-2009 进出口商品容器计重规程 第2部分:动植物油岸上立式金属罐静态计重[S].
[7] 刘新, 赵伟, 俞晔, 等. 密度温度系数对进口精炼棕榈液油计重的影响[J]. 检验检疫学刊, 2015, 25(3): 17-20.
[8] 细矢治夫, 丸山有成. 结构与物性[M]. 方小玉译. 上海: 上海科学技术出版社, 1979: 73-74.
[9] HAYNES W M. CHC Handbook of Chemistry and Physics [M]. 95th ed. Boca Raton: CRC Press, 2014: 6-7– 6-8.
[10] 刘一军, 俞晔. 进口精炼棕榈油温度和密度线性关系的探讨[J]. 中国油脂, 2002, 27(5): 43-45.
(文章类别:CPST-A)







