CopyRight 2009-2020 © All Rights Reserved.版权所有: 中国海关未经授权禁止复制或建立镜像
智能水尺计重测量系统的算法设计
作者:吴璟 杜姗姗 蒋一昕 章回 唐晨
吴璟 杜姗姗 蒋一昕 章回 唐晨
吴 璟 1 杜姗姗 2 蒋一昕 1 章 回 1 唐 晨 1 *
摘 要 针对现有船舶水尺计重过程中存在的主观因素和数据同步性等问题,本研究利用雷达测量技术,通过激光测距仪准确定位,结合三角高程测量法,计算吃水深度。将以上长时间、多点同时测量得到的数字信号用事先预设的算法自动筛选出数据集,计算出结果并形成直观图像。与人工方法比较前后尺总体差异小于0.1%,提高了水尺计重测量的准确性和科学性,有较大的推广应用前景。
关键词 水尺计重;雷达;三角高程测量
Algorithm Design for Intelligent Draft Survey System
WU Jing 1 Du Shan-Shan 2 JIANG Yi-Xin 1 ZHANG Hui 1 TANG Chen 1*
Abstract In view of the subjective factors and data synchronization in the process of draft survey of existing ships, this study uses radar measurement technology, accurate positioning by laser rangefinder, and triangulation elevation measurement method to calculate the draft. The digital signals obtained from long-term, multi-point simultaneous measurements are automatically filtered into a dataset using a pre-set algorithm. Subsequently, the results are calculated and visualized as an intuitive image. Compared with manual methods, the overall discrepancy of the two draft survey before and after is less than 0.1%, which enhances the accuracy and scientific reliability of draft surveys, presenting significant potential for widespread adoption.
Keywords draft survey; radar; trigonometric leveling
水尺计重作为散货船运输中普遍采用的一种货物计重方法,具有省时省力、低成本、高效率等优点[1],进口铁矿石、铜精矿、煤炭、大豆、粮食等关系到国计民生的大宗商品基本都采用水尺计重的方式[2],其计算结果是货物通关计税、交接结算、理赔计费的重要依据[3]。因此,通过技术手段和现场检验人员的规范操作来减小水尺观测的误差是提高水尺计重准确度的重要突破口[4]。
国内外现有的水尺观测方法大致分为三类,即人工观测、基于机器视觉的智能观测和传感器测量。传统水尺鉴定一般采用人工观测法,主要依靠检验人员的经验来决定数据的读取,人的主观因素对鉴定结果影响很大,手工记录的数据也无法进行事后查验校对。近年来,行业内开始尝试采用基于机器视觉的智能观测法,使用钓竿、无人机[5-6]、无人船[7]、机器人[8]等测量平台采集水位测量点附近的图像信息,通过智能算法获得水尺数据,测量的智能化程度高于传统的人工目测方法,但是这些测量方案受环境限制,在保证全天候作业方面还存在挑战,且对图像信号处理的效果也不甚理想[9-10]。基于传感器的测量方法与上述两种方案不同,可以直接获得数字信号,便于测量数据的读取和处理,但是因船型引起的船艏和船艉高度差校正困难限制了该类方法的推广应用[11]。以上这些测量方法均采用单点依次测量的方式,每个测量点的观测时间很短,但整体的测量周期很长,在全部6点水尺观测的周期内来自不同方向的波浪严重影响了船舶全身水尺观测的同步性,后期的数据处理也仅是单个测量点数据的简单平均,难以反应同一时间内船舶真实的六面吃水情况,从而可能造成一定测量误差。
为进一步提升测量方法的准确性,本研究基于雷达、激光测距和无线通信技术,研发了一种全天候、全场景的智能水尺测量设备,并在此基础上开发出一种多维度优化的数据处理方案。
1 设计原理与方法
1.1 总体技术路线
本研究利用便携式电磁波雷达测量水面空距,再利用激光测距仪定位雷达测量面与水尺标记的高度差,结合上述的水面空距、高度差、船舶水尺标记读数,通过三角高程测量法计算出实际吃水深度值。同时,通过远距离无线通信(Long Range Radio,LoRa)技术和实验室虚拟仪器工程平台(Laboratory Virtual Instrument Engineering Workbench,LABVIEW)进行信号的传输和设备的远程控制,实现水尺计重过程中长时间、全方位、全自动测量。
本研究利用上述设备获取船舶艏部、舯部、艉部左右舷水尺标记位置的6点瞬时测量数据,并由此6点数据计算得到的船艏横倾、船舯横倾、船艉横倾、左舷艏艉纵倾和右舷艏艉纵倾5点数据,共同组成了11维数据集,并以连续的曲线形式直观地呈现在计算机屏幕上,综合比较其稳定性变化程度,根据水面波动与船舶姿态变化的规律,分别设计加权法和叠加法用于自动筛选及推荐数据采集区间,利用各个推荐区间的数据分别计算6点水尺平均值,检验人员根据现场情况和曲线确定6点的最终的吃水值。总体技术路线如图1所示。
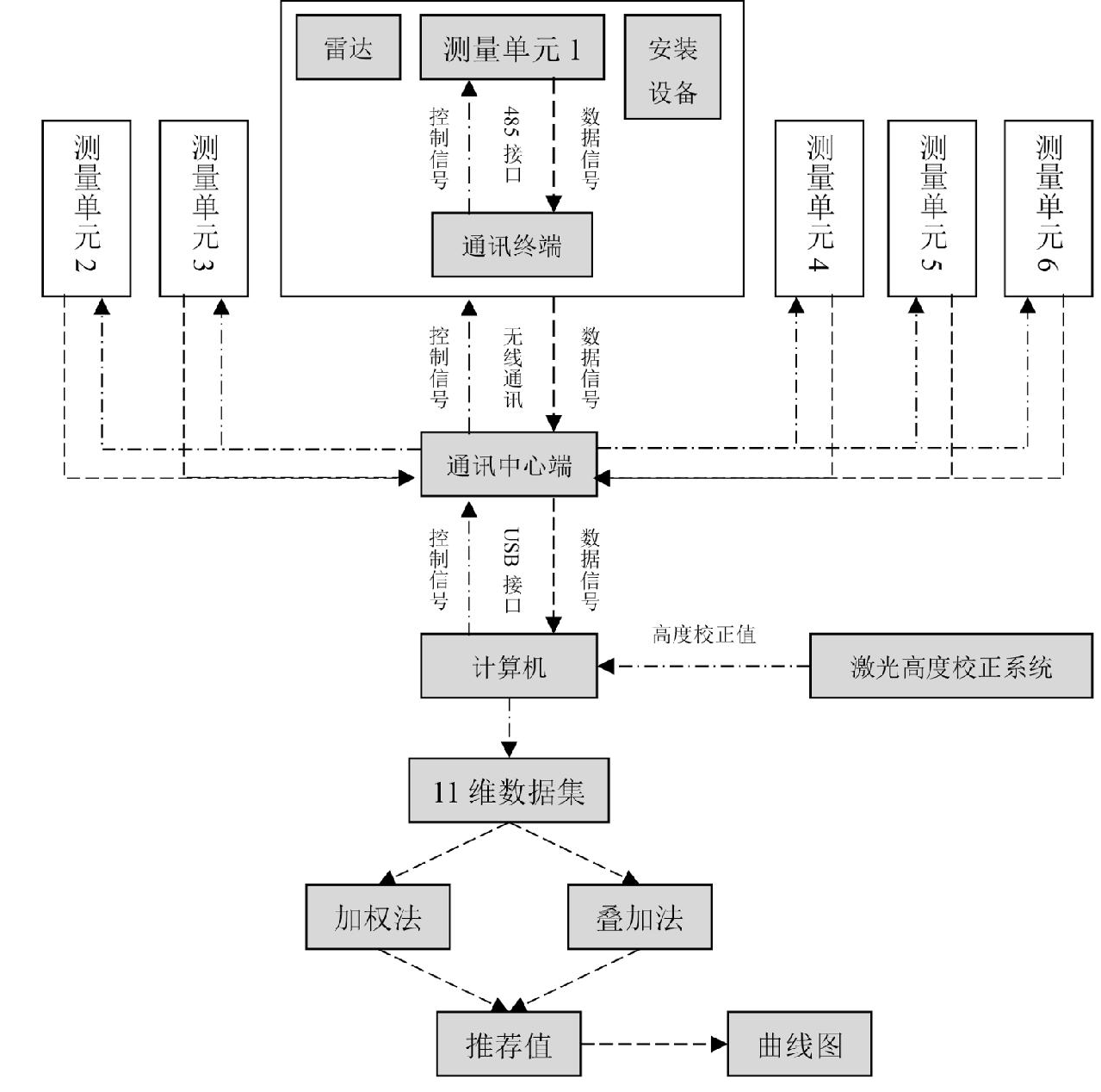
图1 总体技术路线图
Fig.1 Overall technical roadmap
1.2 水位测量系统设计
(1)鉴于水尺测量现场环境的特殊性,本研究选用了调频连续波雷达(Frequency Modulated Continuous Wave Radar,FMCW)作为测量单元,有效解决了测量现场舱壁和岸基带来的测距干扰,如图2所示。
(2)为了解决雷达测量结果传输到控制平台所面临的空间跨度、电磁干扰、电源、布线等问题,本研究选择采用LoRa(Long Range Radio)方式进行无线通信[12],如图3所示。组网通信系统由计算机终端、作为中心节点的通信基站、作为终端节点的通信模块等组成。输入端的外部仪器通过RS485串口总线与LoRa通信系统连接,输出端LoRa通信系统通过USB接口与PC实现通信。采用LoRa通信协议进行组网通信,实现命令或参数的下达,以及数据的采集与上传等功能。
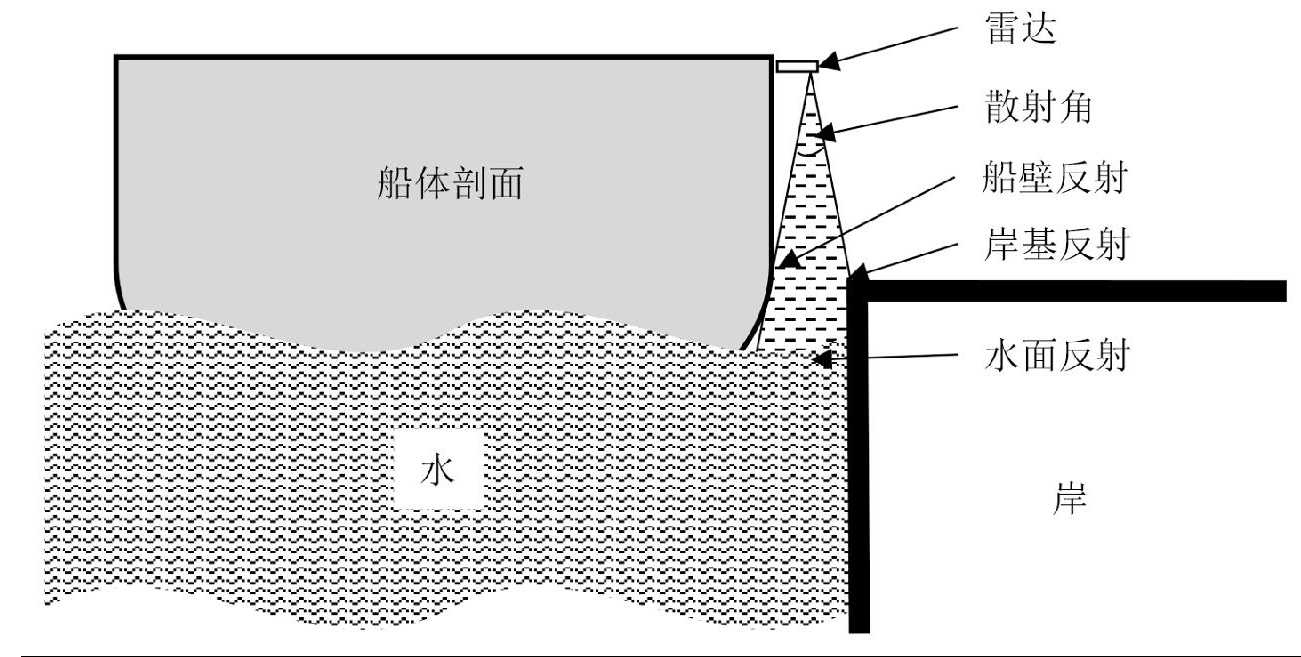
图2 雷达反射面示意图
Fig.2 Schematic diagram of radar reflector
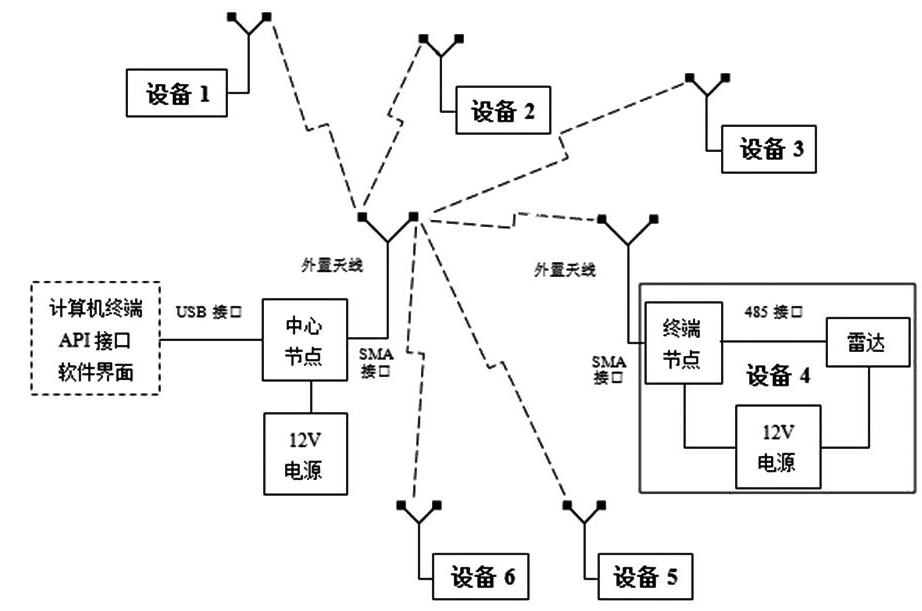
图3 通信网络结构图
Fig.3 Structure diagram of communication network
(3)仪器控制系统是利用虚拟仪器专用开发平台LabVIEW,应用动态链接库通过USB接口与外部仪器通信,并且有菜单可以实现常用功能的操作。软件的主界面主要分为工具栏、菜单栏以及参数输入、运行控制和数据显示区域,如图4所示。
测量前在参数输入部分输入有关参数,在控制部分输入测量时间或直接开关测量设备,数据显示区域可以实时显示被测量的6个吃水点数据以及纵横倾曲线。
1.3 吃水深度算法设计
1.3.1 单点单次测量吃水值的计算方法
使用移动式雷达或激光装置测量船舶吃水值时,最关键的是确定测量参考基点。船舶载重线标志勘绘于船中两舷船壳外板,可从船舶资料中获取其高度作为测量参考基点,如甲板线对应的型深 。传统方案中,测量吃水值时,需要将测量装置准确地安装在与甲板线上缘齐平的位置,测定装置至水面的距离
。传统方案中,测量吃水值时,需要将测量装置准确地安装在与甲板线上缘齐平的位置,测定装置至水面的距离 ,利用
,利用 减去
减去 ,得到吃水深度
,得到吃水深度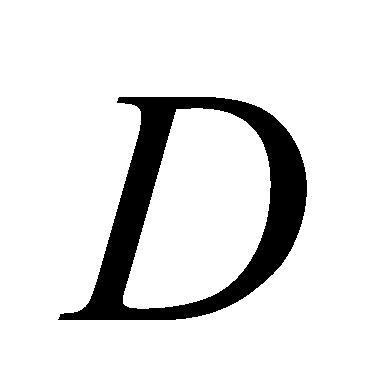 ,如图5所示。
,如图5所示。
然而,实践中存在两个关键问题影响吃水深度的测算:(1)由于船舶艏艉通常没有勘绘相关标志,艏艉吃水深度无法测算;(2)测量装置的安装需要与甲板线上缘齐平,安装固定存在一定的困难。
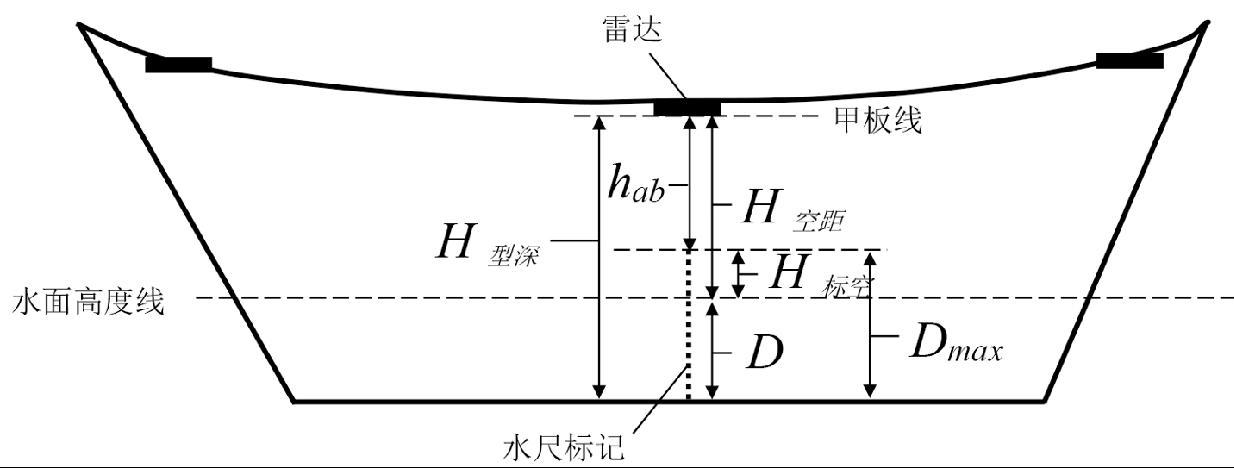
图5 吃水深度计算示意图
Fig.5 Schematic diagram of draft calculation
鉴于上述两点问题,本文作者采用三角高程中间测量法[14],以艏、舯、艉水尺标记最高刻度线的下缘作为测量参考基点,使用雷达和激光测距仪进行相关参数的测量,再计算出各个测量点的水尺读数,具体步骤如下:
(1)人工读取水尺刻度标记最高点下缘值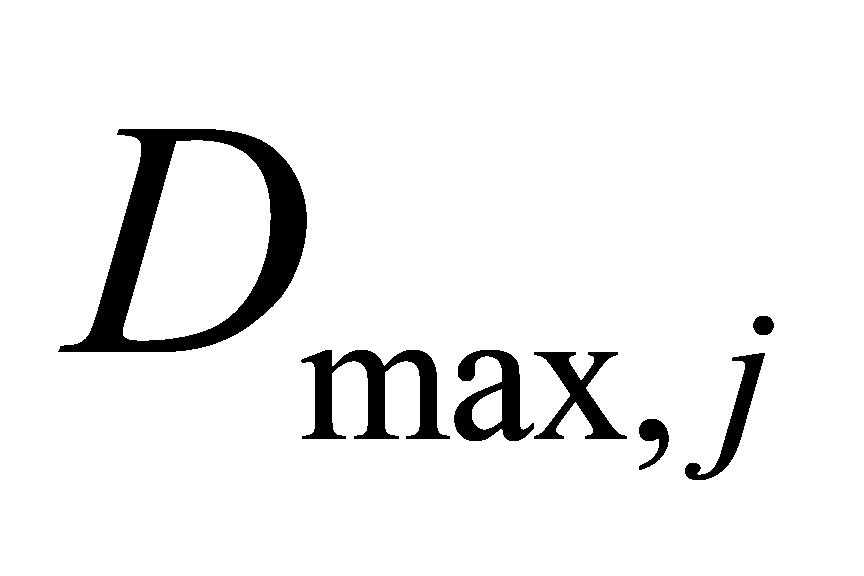 (j为数据系列序号,具体对应关系见表1,下同,此处仅涉及1—6)。
(j为数据系列序号,具体对应关系见表1,下同,此处仅涉及1—6)。
(2)在水尺刻度标记正上方,使用调频连续波雷达(FMCW)测量其与水面高度差 。
。
(3)如图6所示,在岸上利用激光测距仪测量得其与a点的距离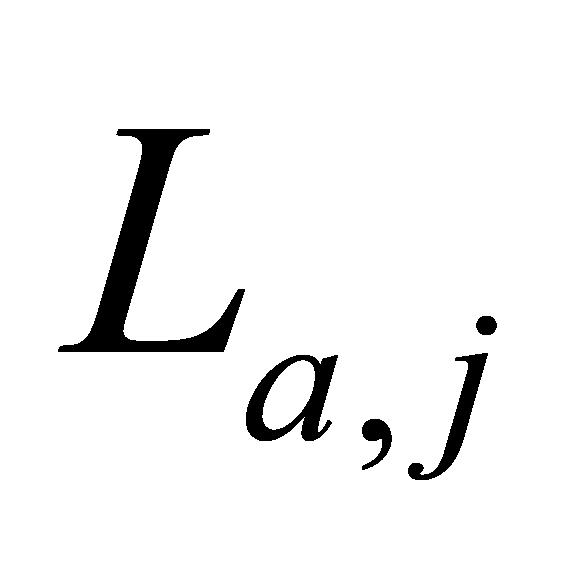 和角度
和角度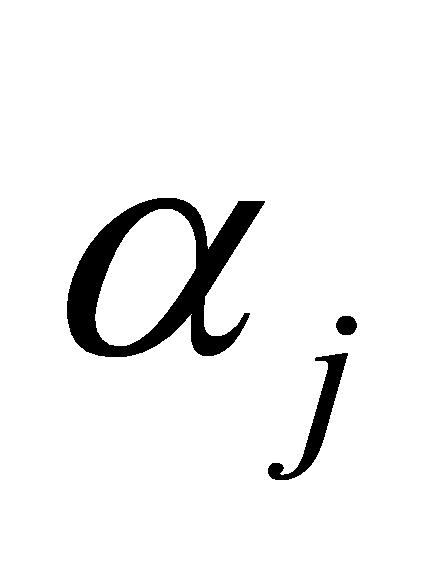 ,以及与b点的距离
,以及与b点的距离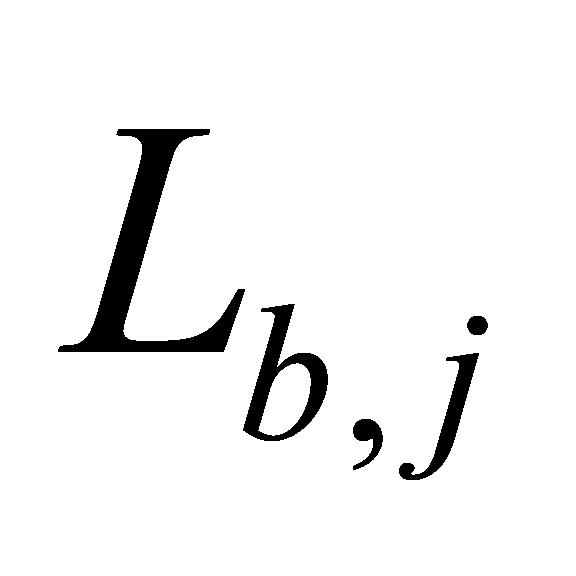 和角度
和角度 ,分别计算a点至激光测距仪的垂直高度
,分别计算a点至激光测距仪的垂直高度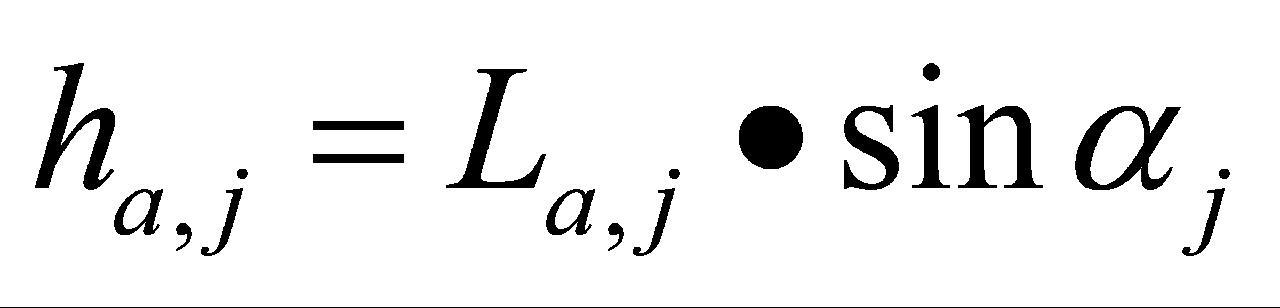 和b点至激光测距仪的垂直高度
和b点至激光测距仪的垂直高度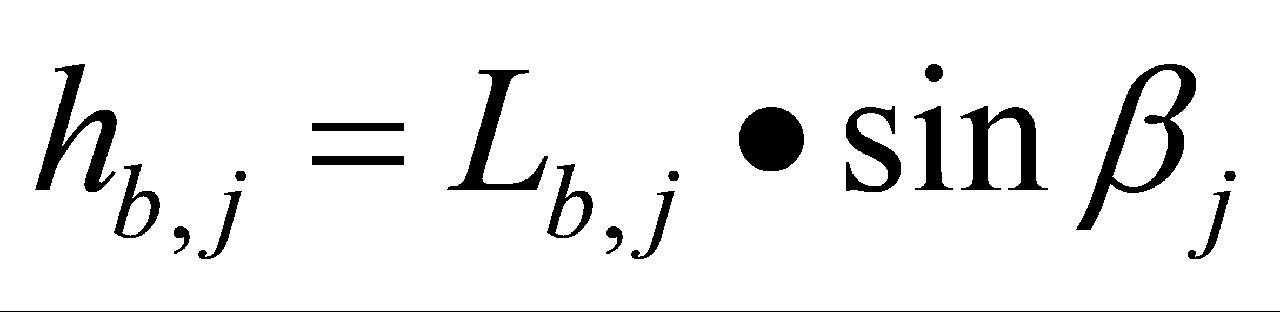 。
。
(4)计算a、b两点垂直高度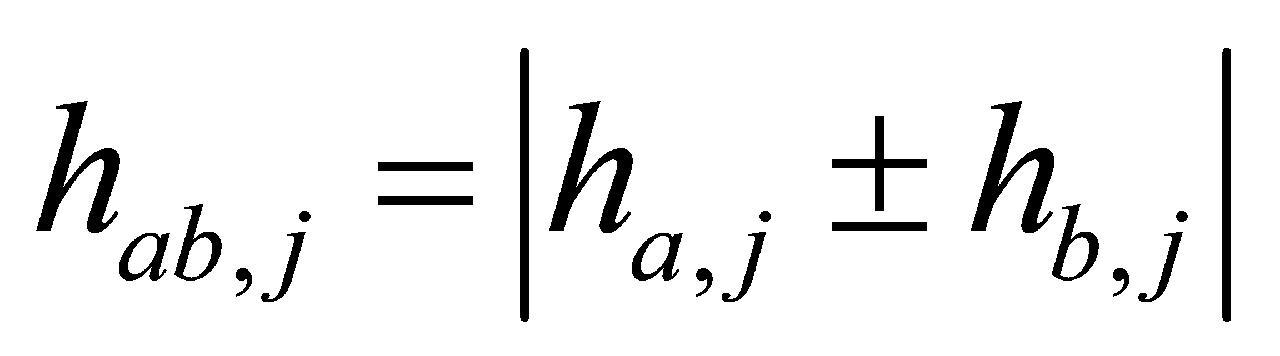 ,a、b点同在激光测距仪上方或下方则运算符号为“-”。
,a、b点同在激光测距仪上方或下方则运算符号为“-”。
(5)计算水尺刻度标记最高点下缘与水面高度差 。
。
(6)计算吃水深度 。
。
1.3.2 数据筛选算法设计
船舶停靠在水面上,吃水值受到风浪、涌浪、船舶姿态和船舶作业状态等多种因素的影响,始终处在动态变化的过程中。由于水的流体特性,造成了水位与船舶姿态变化的不同步,当水位发生变化时,6点吃水立即随之变化,而船舶姿态需要经过一段时间之后才随之发生变化,船舶姿态主要由纵横倾数值反映,因此纵横倾值的变化明显滞后于6点吃水的变化。实际情况是水位和船舶姿态变化不断交替,反复多次后才达到新的平衡,在此过程中新一轮波动又不断叠加到前一个波动中,所以实际的吃水值和纵横倾变化很难用一个简单的公式或图表进行描述,只能用统计的方式给出趋近于平衡态的吃水结果[15],具体步骤如下:
(1)在船艏左右、船艉左右和船舯左右6个点位安装测量设备并同步实时测量,测得值按照1.3.1所述方法计算,得到6组吃水值数据,每组吃水值随时间变化曲线如图7所示,定义一个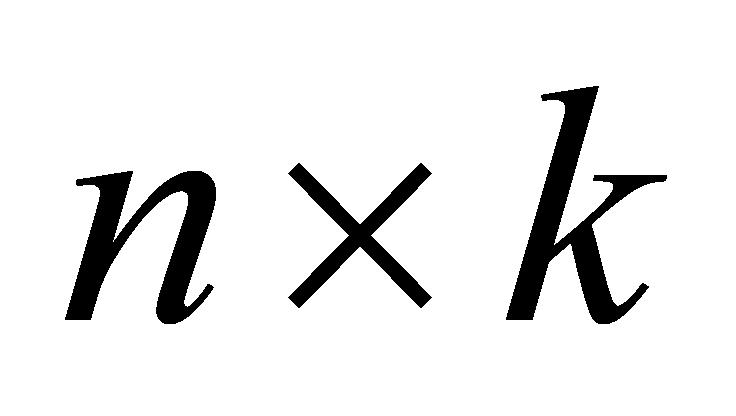 的
的 矩阵,如公式(1)所示,上述6组数据构成
矩阵,如公式(1)所示,上述6组数据构成 矩阵的前6列。
矩阵的前6列。
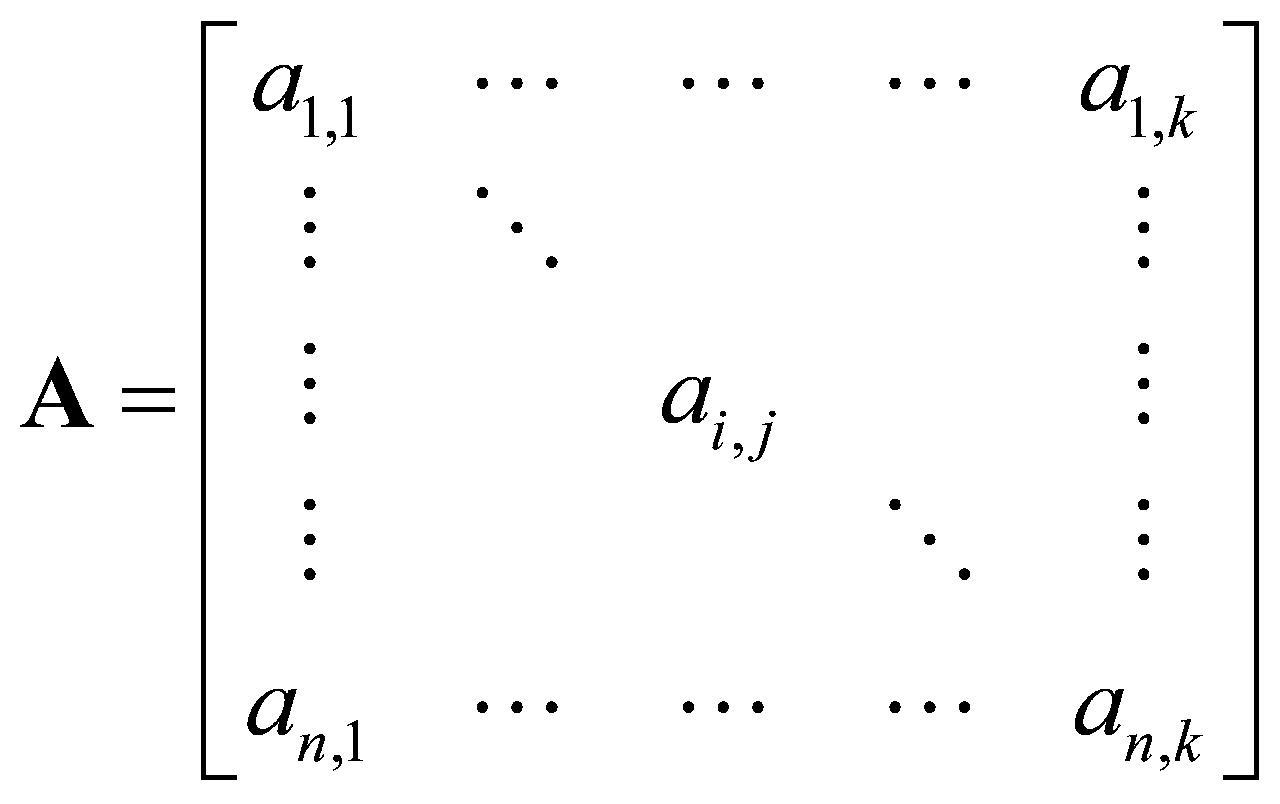 (1)
(1)
式(1)中,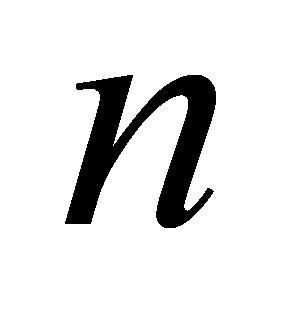 为测量时间内依次采集的数据个数,即
为测量时间内依次采集的数据个数,即 矩阵行数;
矩阵行数;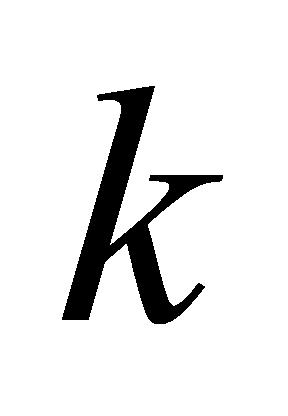 为数据组数量,即
为数据组数量,即 矩阵列数,
矩阵列数,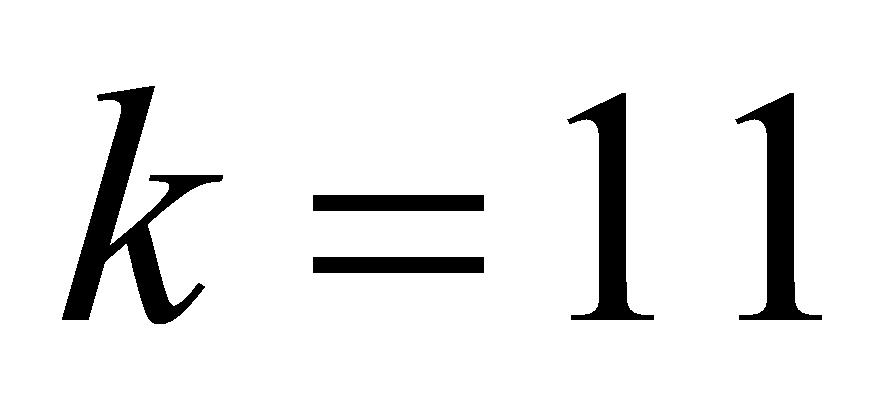 ;
; 为
为 矩阵中的数据点;i为行序号,
矩阵中的数据点;i为行序号, ;j为数据系列序号,对应关系见表1。
;j为数据系列序号,对应关系见表1。
(2)根据上述6组吃水数据,按公式(2)至(4)计算船舶艏、舯、艉左右横倾值系列数据,按公式(5)至(6)计算船舶左、右艏艉纵倾值,得到另外5组数据,随时间变化曲线如图8所示,该5组数据构成 矩阵的后5列。
矩阵的后5列。
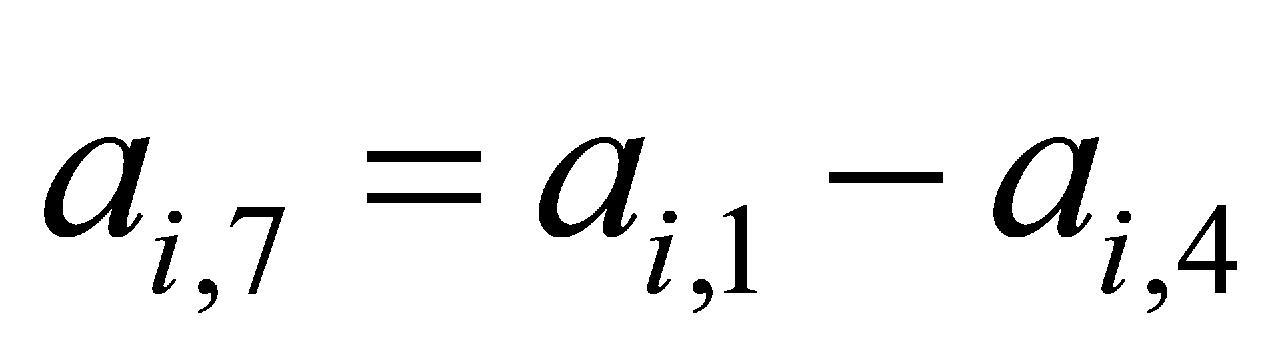 (2)
(2)
 (3)
(3)
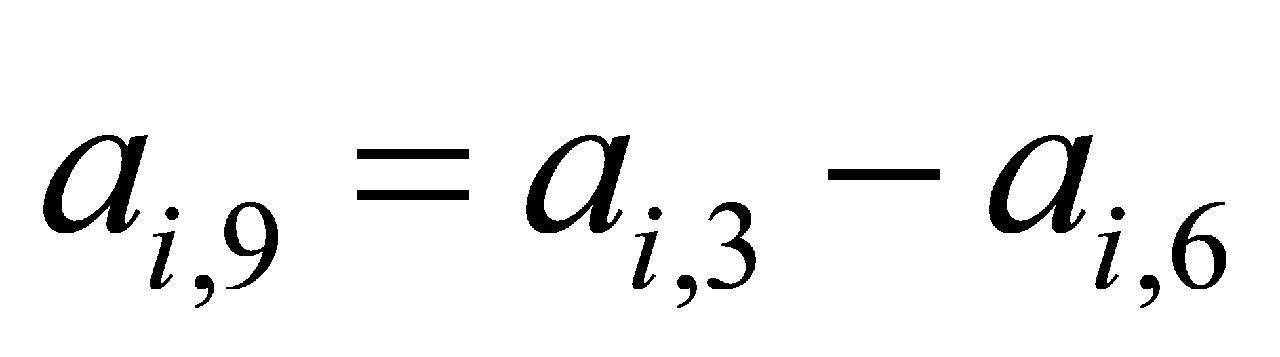 (4)
(4)
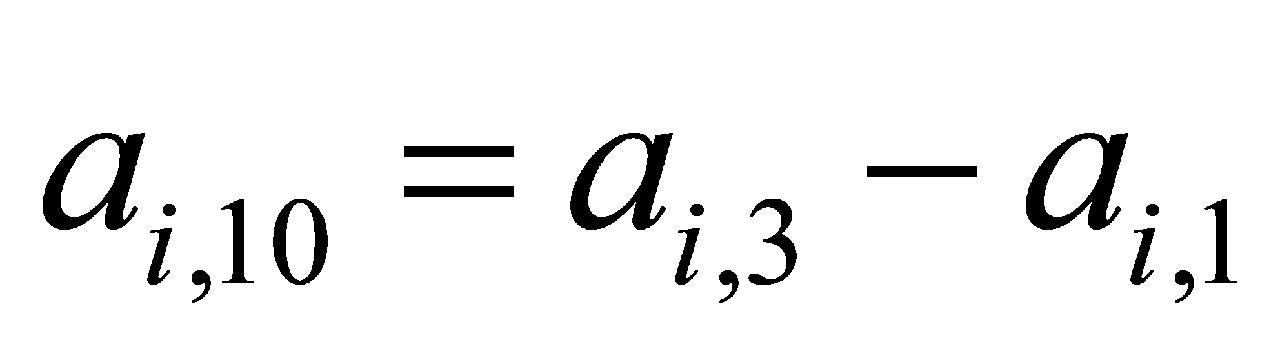 (5)
(5)
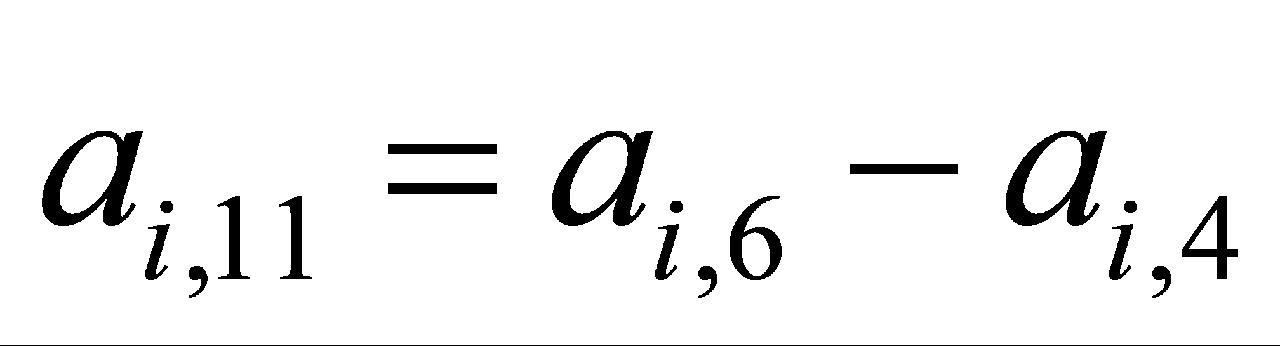 (6)
(6)
式(2)—式(6)中: 为船艏横倾值系列数据;
为船艏横倾值系列数据; 为船舯横倾值系列数据;
为船舯横倾值系列数据;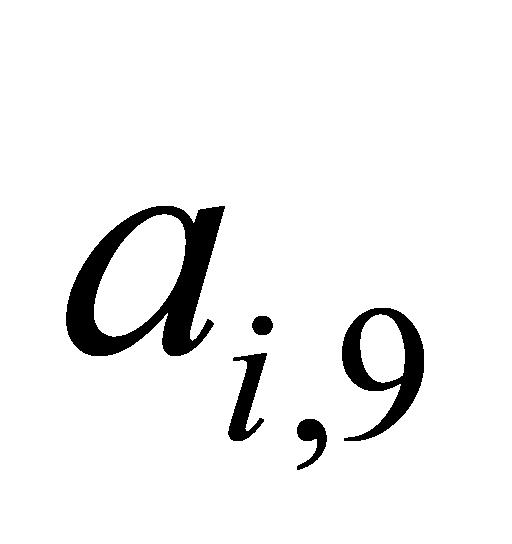 为船艉横倾值系列数据;
为船艉横倾值系列数据; 为船左纵倾值系列数据;
为船左纵倾值系列数据;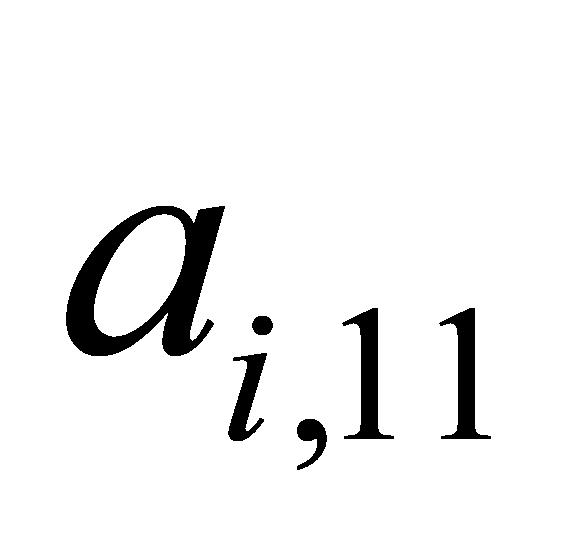 为船右纵倾值系列数据。
为船右纵倾值系列数据。
(3)依据公式(7)依次计算 矩阵中每列连续的20个数据的标准偏差,得到
矩阵中每列连续的20个数据的标准偏差,得到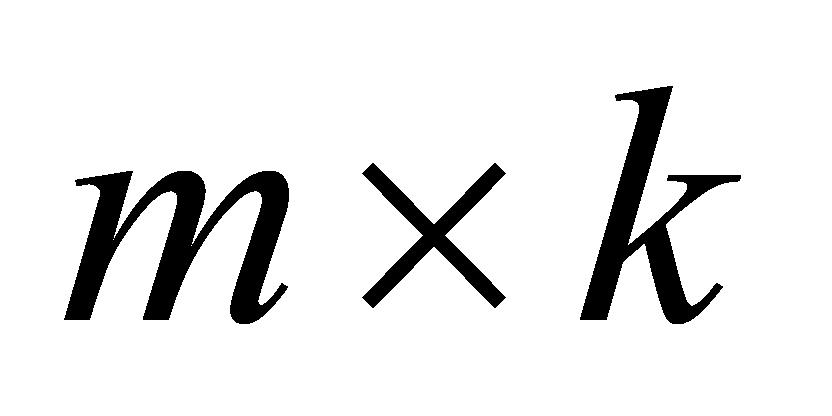 的
的 矩阵,如式(8)所示:
矩阵,如式(8)所示:
 (7)
(7)
 (8)
(8)
式(7)至式(8)中: 为
为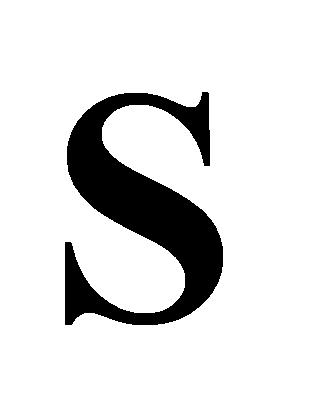 矩阵中的数据点;x为矩阵行序号,
矩阵中的数据点;x为矩阵行序号, ;j为数据系列序号,同上文;
;j为数据系列序号,同上文;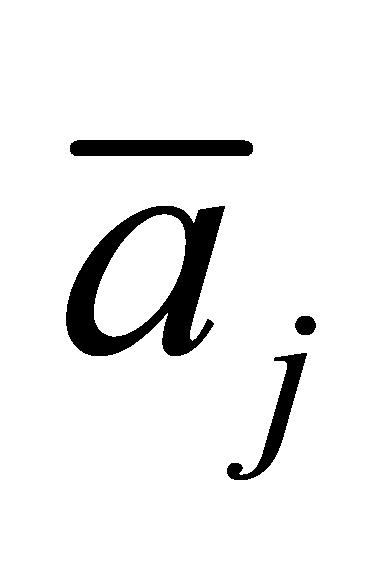 为每20个连续数据的平均值;
为每20个连续数据的平均值;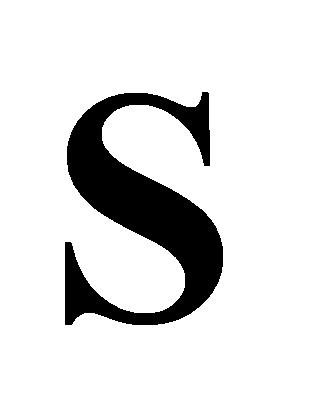 矩阵与
矩阵与 矩阵列序号相互对应,用
矩阵列序号相互对应,用 矩阵中每列连续的20个数据为一组计算标准偏差,因此
矩阵中每列连续的20个数据为一组计算标准偏差,因此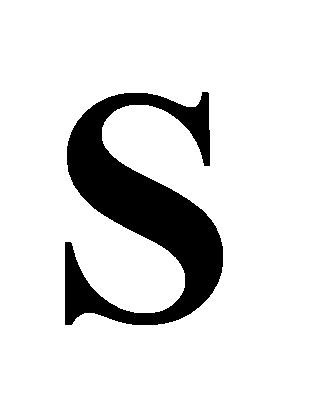 矩阵比
矩阵比 矩阵少19列,
矩阵少19列, 。
。
(4)两种数据筛选算法
A.叠加法:分别比较11维数据的变异性,选取变异性均小于某个设定值的数据作为采集区间,取其平均值。
(A-1)调用 函数,依据公式(9)计算
函数,依据公式(9)计算 矩阵中每列的
矩阵中每列的 分位点的数值
分位点的数值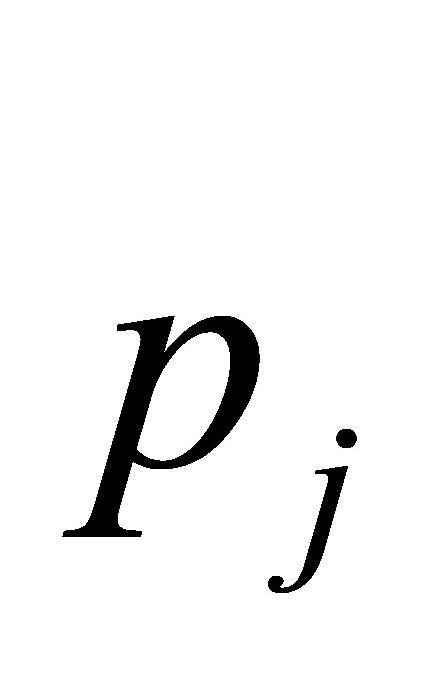 ,本研究采用30%分位点上的数值,则
,本研究采用30%分位点上的数值,则 设为0.3。
设为0.3。
 (9)
(9)
式(9)中, 为
为 矩阵中第
矩阵中第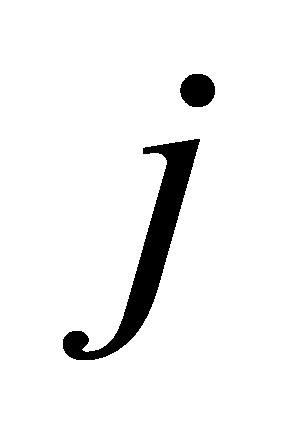 列的第1行数据;
列的第1行数据;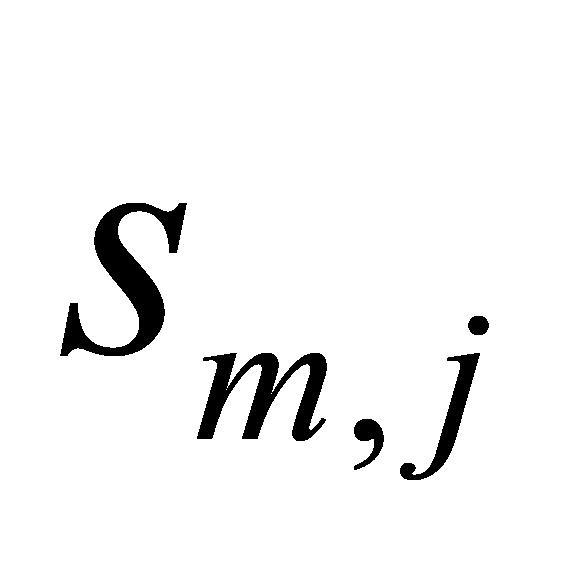 为
为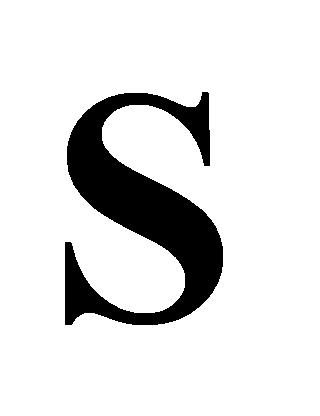 矩阵中第
矩阵中第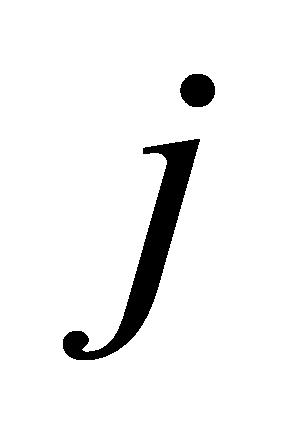 列的最后一行数据;
列的最后一行数据;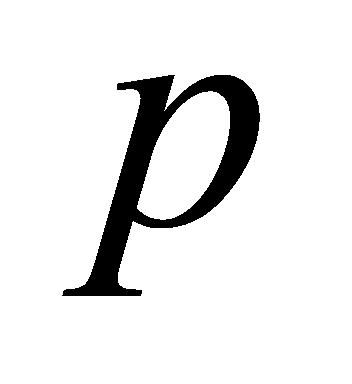 为设定的分位点,
为设定的分位点,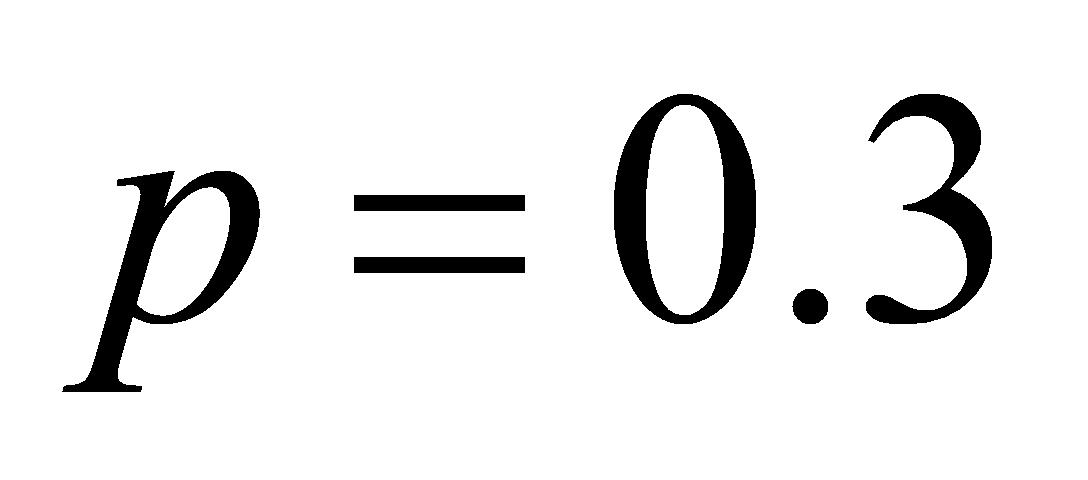 。
。
(A-2)比较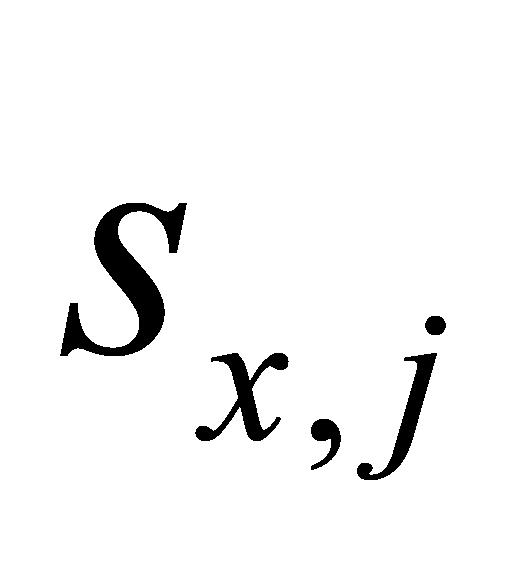 与
与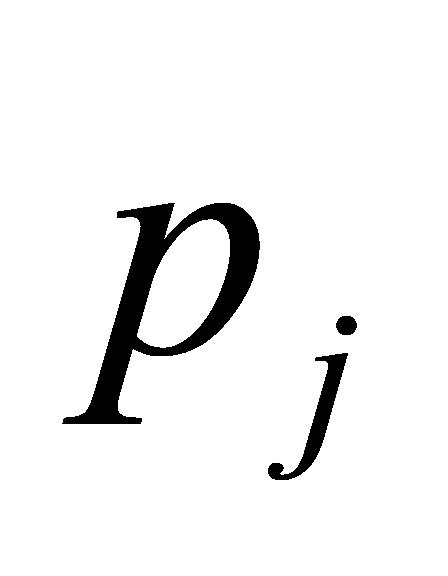 的大小,确定变异性排名符合设定要求的数据,由公式(7)可以推断出,当
的大小,确定变异性排名符合设定要求的数据,由公式(7)可以推断出,当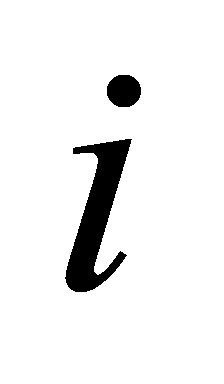 为某一具体数值时(
为某一具体数值时(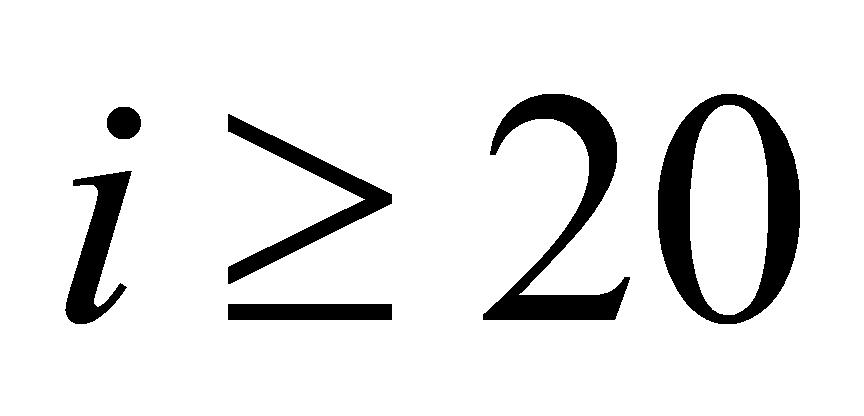 ),
), 参与了
参与了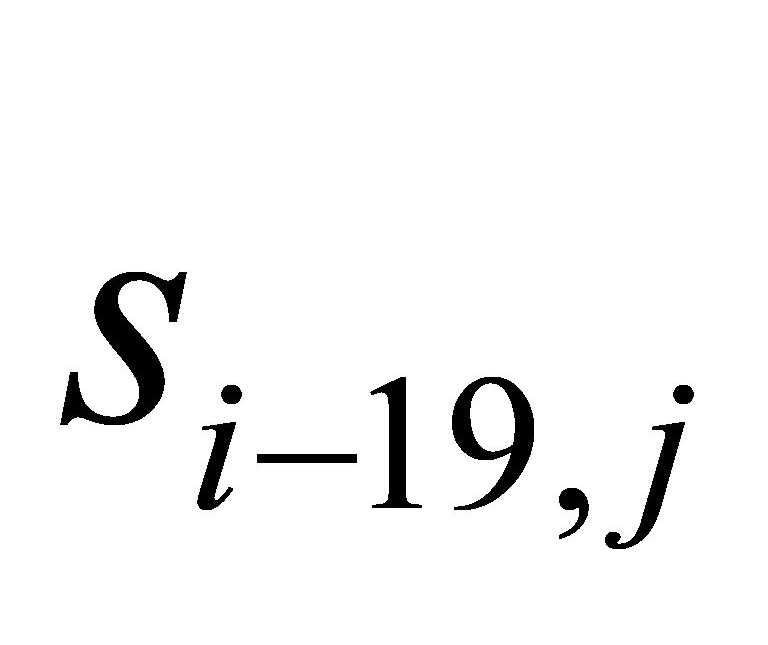 至
至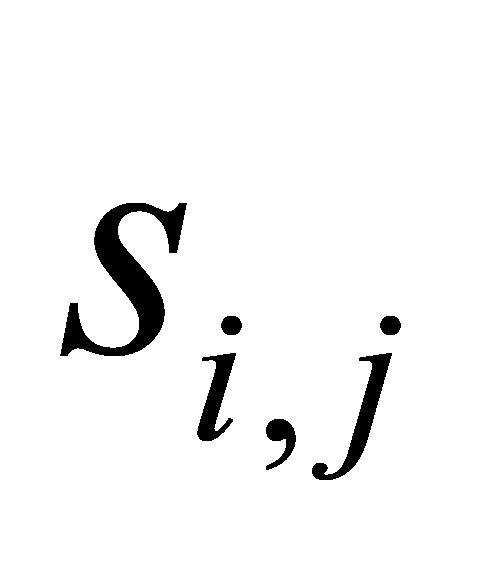 共20个
共20个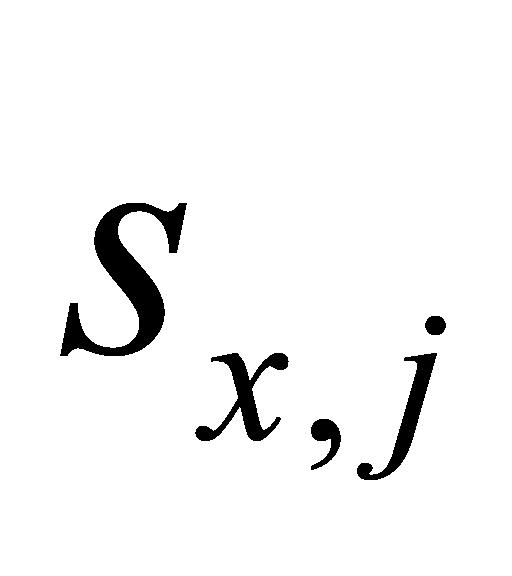 的计算,如式(10)所示。因此,当
的计算,如式(10)所示。因此,当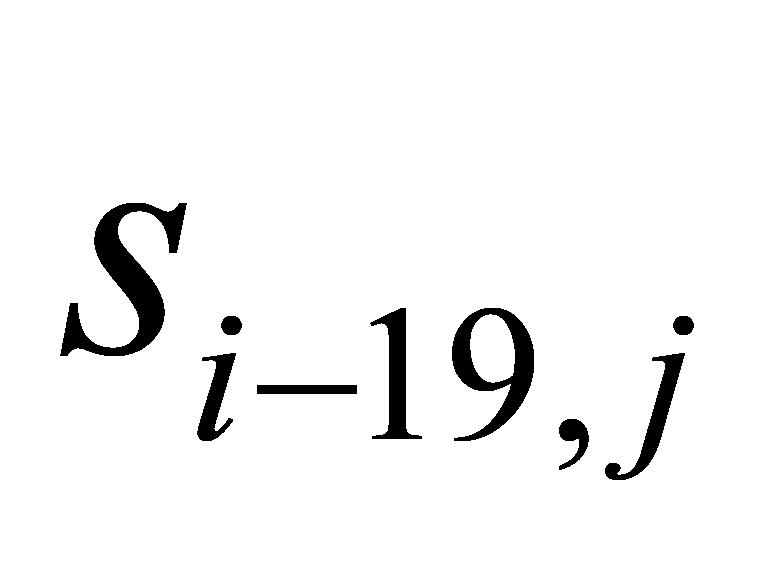 至
至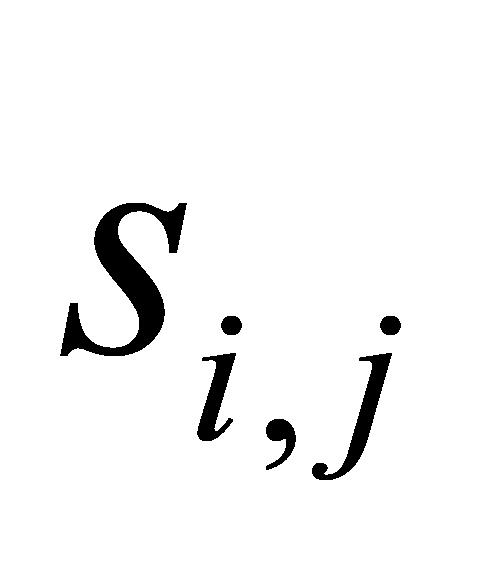 共20个
共20个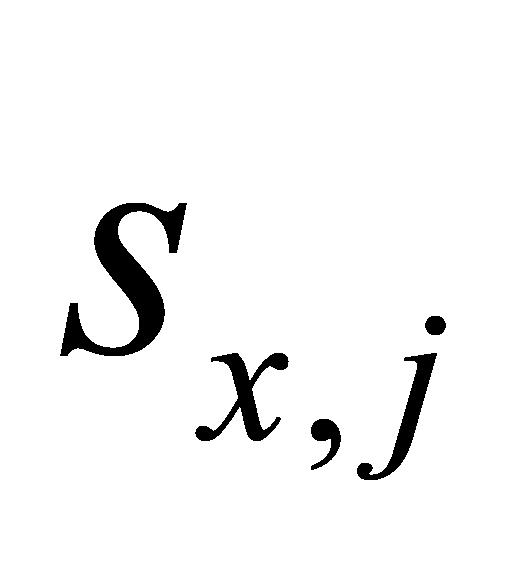 之中存在小于
之中存在小于 的数值时,
的数值时, 可被认为是符合变异性要求的,赋值
可被认为是符合变异性要求的,赋值 矩阵中对应的元素
矩阵中对应的元素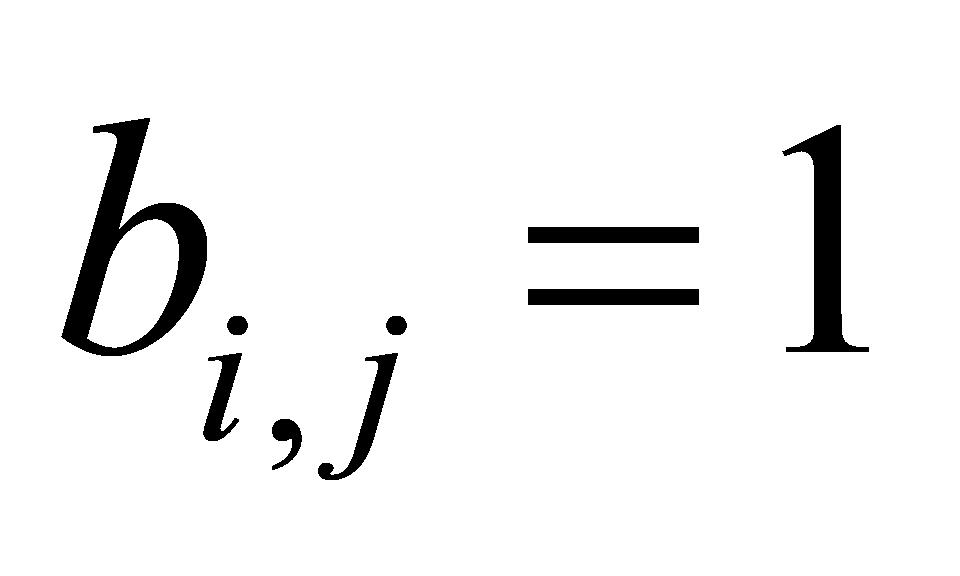 ,此
,此 矩阵的规模与
矩阵的规模与 矩阵相同,在
矩阵相同,在 的情况下,
的情况下, 应赋值0。
应赋值0。
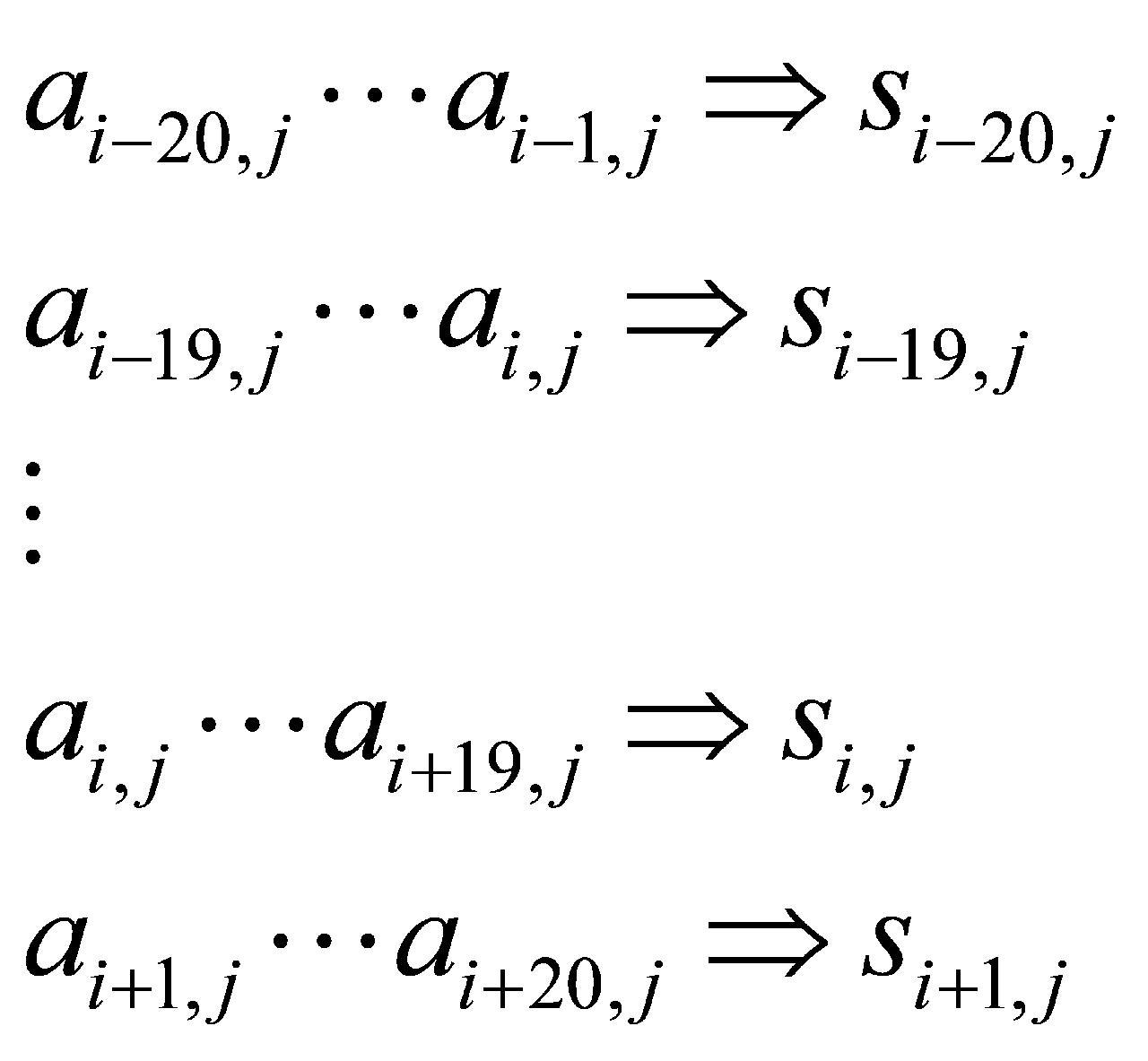 (10)
(10)
(A-3)将 矩阵中每行数据连乘,得到
矩阵中每行数据连乘,得到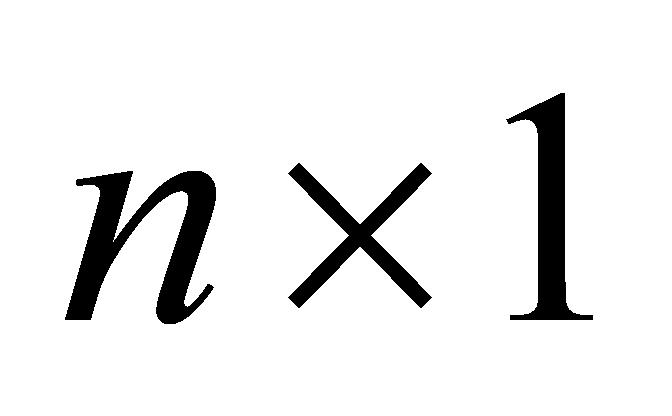 规模的
规模的 矩阵,矩阵中的元素
矩阵,矩阵中的元素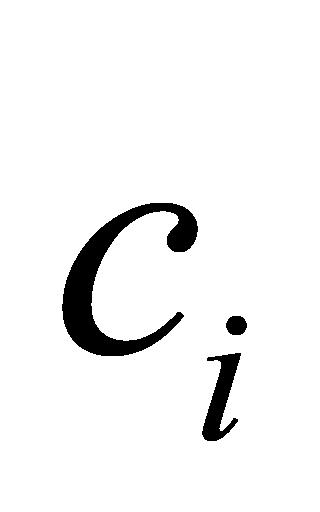 的值只有0或1,其中为1的位置就是11个维度的变异性全部小于设定值的测量时间点。
的值只有0或1,其中为1的位置就是11个维度的变异性全部小于设定值的测量时间点。
(A-4)使用公式(11)计算各个观测点的最终的吃水值 ,此时
,此时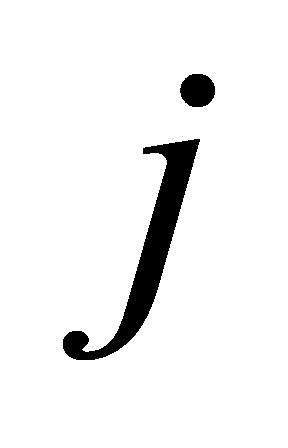 只需要取1~6。
只需要取1~6。
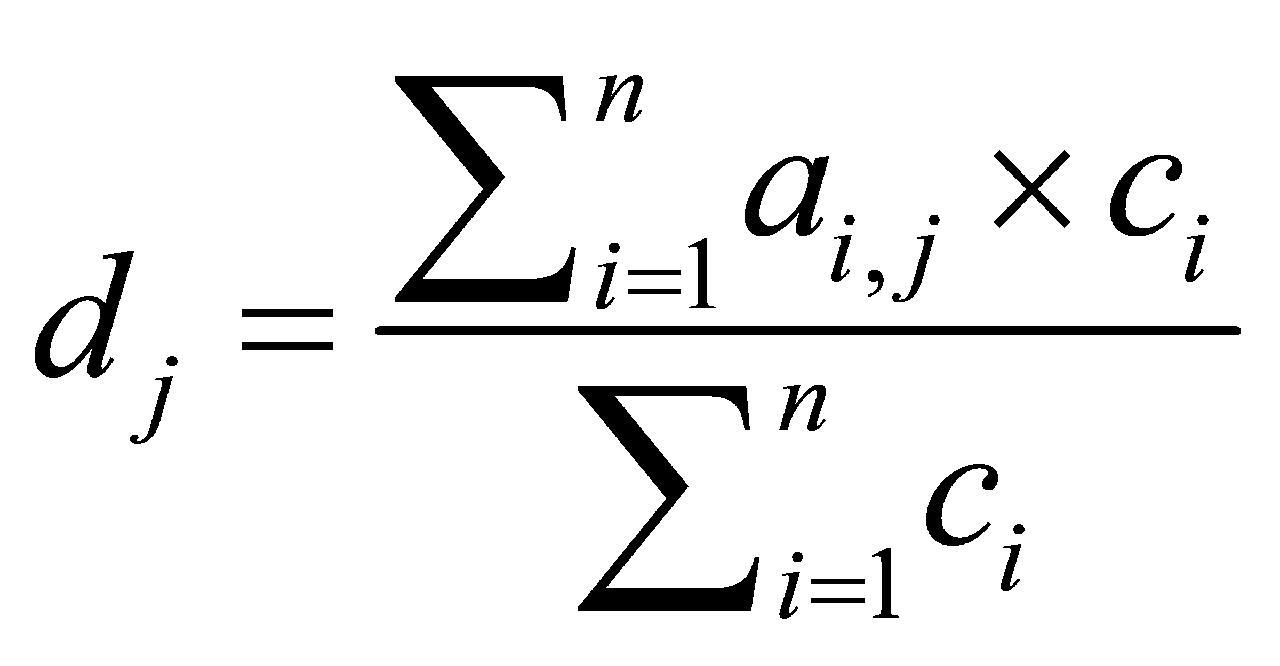 (11)
(11)
B.加权法:按照分配的权重综合比较各维度数据的变异性,选取综合变异性小于设定值的数据作为采集区间,取其平均值。
(B-1)首先为11组数据按重要性分配权重,见表2。
其中权重分配的主要依据是该组数据对水尺计算结果的影响程度和对水面波动的反应程度,经反复测试比较,得到表2中的数据,比较能够真实反映出波动程度并有利于筛选出有效数据。
根据表2定义一个 的权重矩阵
的权重矩阵 ,对
,对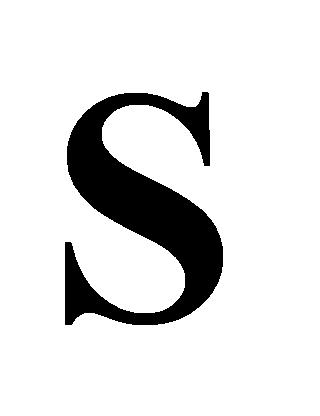 矩阵每行数据依据公式(12)进行计算,得到每行数据加权后的标准偏差之和,形成一个
矩阵每行数据依据公式(12)进行计算,得到每行数据加权后的标准偏差之和,形成一个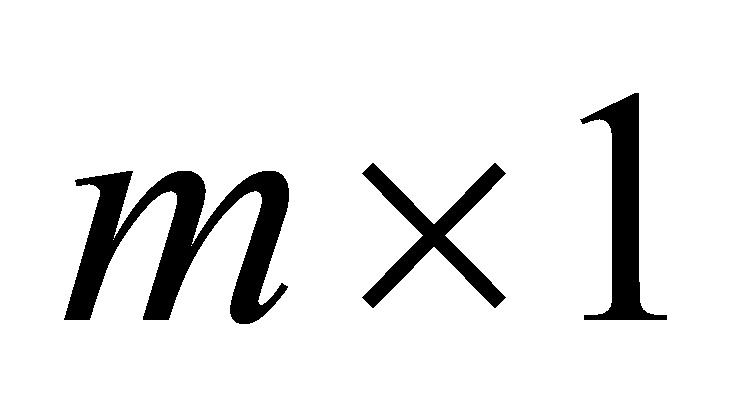 规模的
规模的 矩阵,矩阵元素为
矩阵,矩阵元素为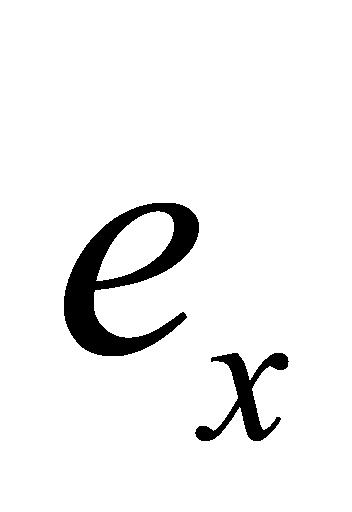 ;
;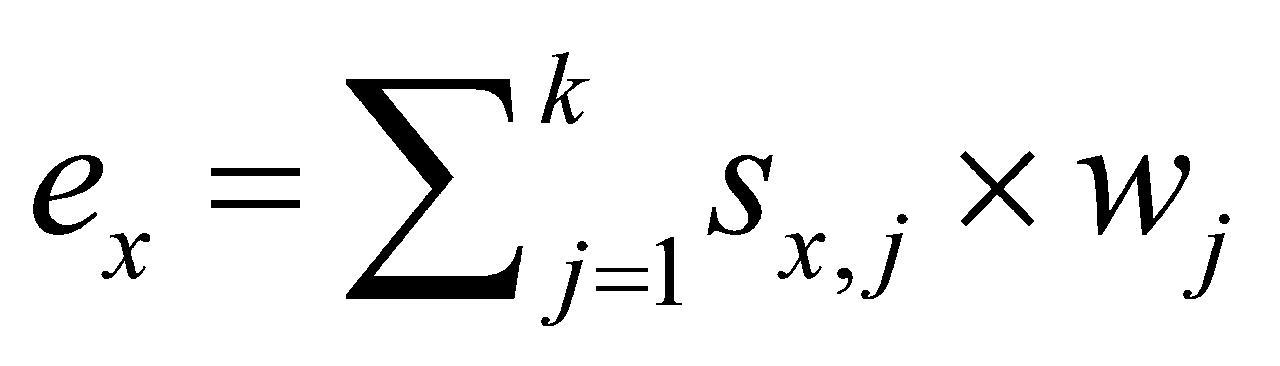 (12)
(12)
式(12)中, 为每一列标准差数据对应的权重。
为每一列标准差数据对应的权重。
(B-2)按照(A-1)所述方法计算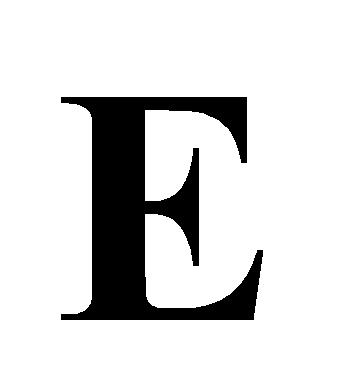 矩阵的
矩阵的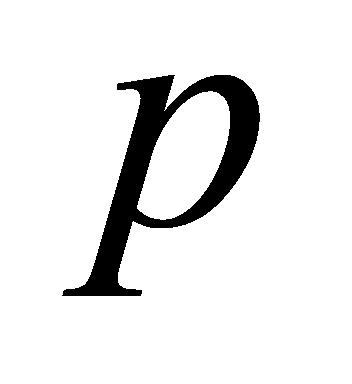 分位点的数值
分位点的数值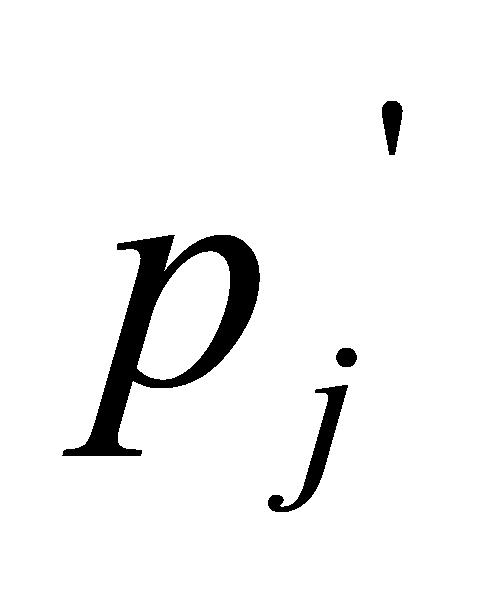 ,
,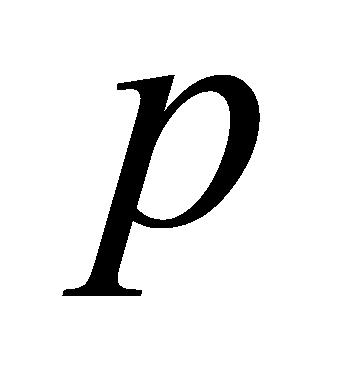 设为0.2。
设为0.2。
(B-3)依据(A-2)所述筛选原理,比较 与
与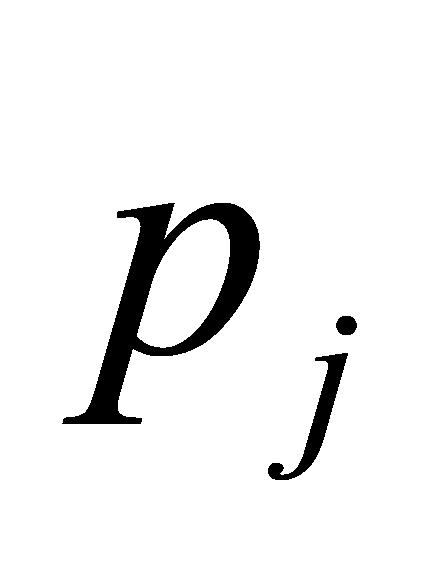 的大小,确定变异性排名符合设定要求的数据,当
的大小,确定变异性排名符合设定要求的数据,当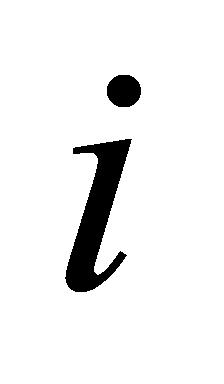 为某一具体数值时(
为某一具体数值时( ),由于
),由于 参与了
参与了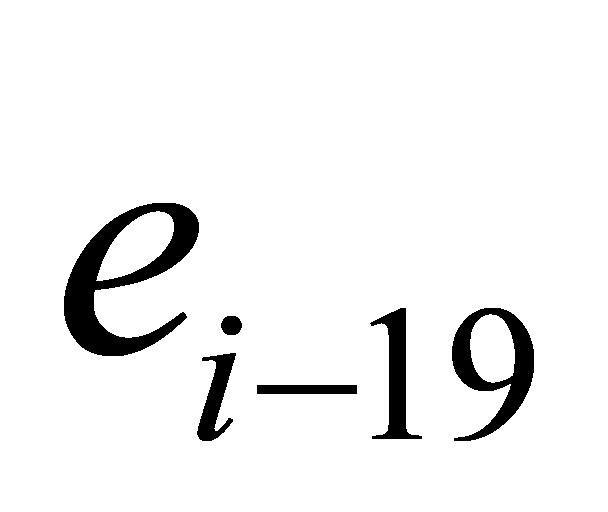 至
至 共20个
共20个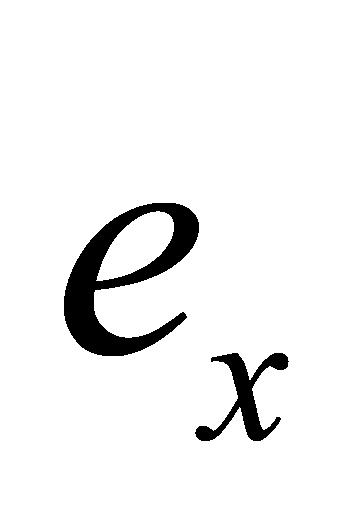 的计算。因此,当
的计算。因此,当 至
至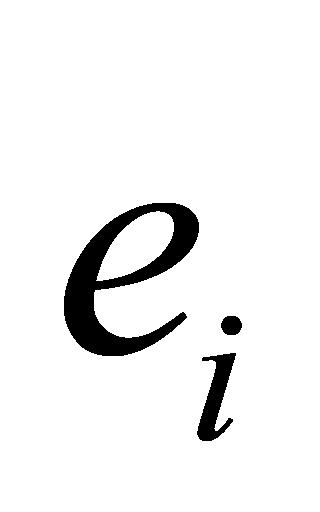 共20个
共20个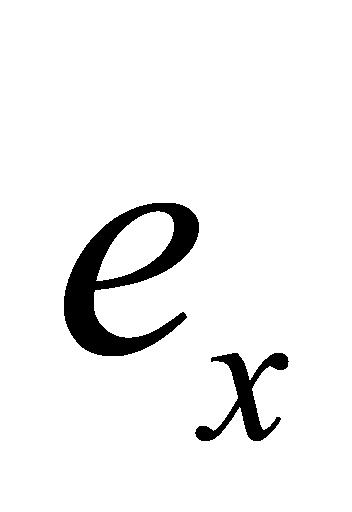 之间存在小于
之间存在小于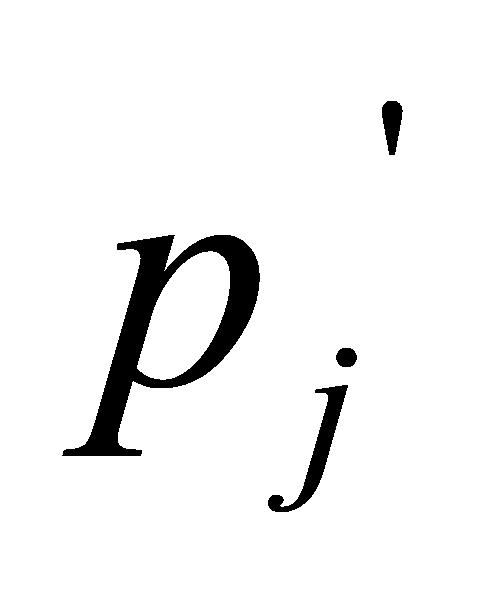 的数值时,
的数值时, 可被认为是符合变异性要求的,赋值
可被认为是符合变异性要求的,赋值 矩阵中对应的元素
矩阵中对应的元素 ,在
,在 的情况下,
的情况下, 应赋值0。
应赋值0。
(B-4)使用公式(13)计算各个观测点的最终的吃水值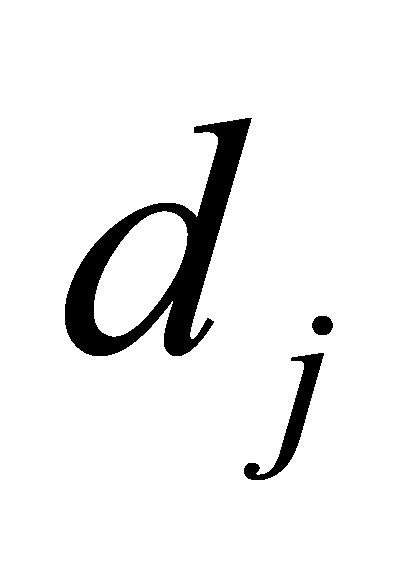 ,此时
,此时 只需要取1~6。
只需要取1~6。
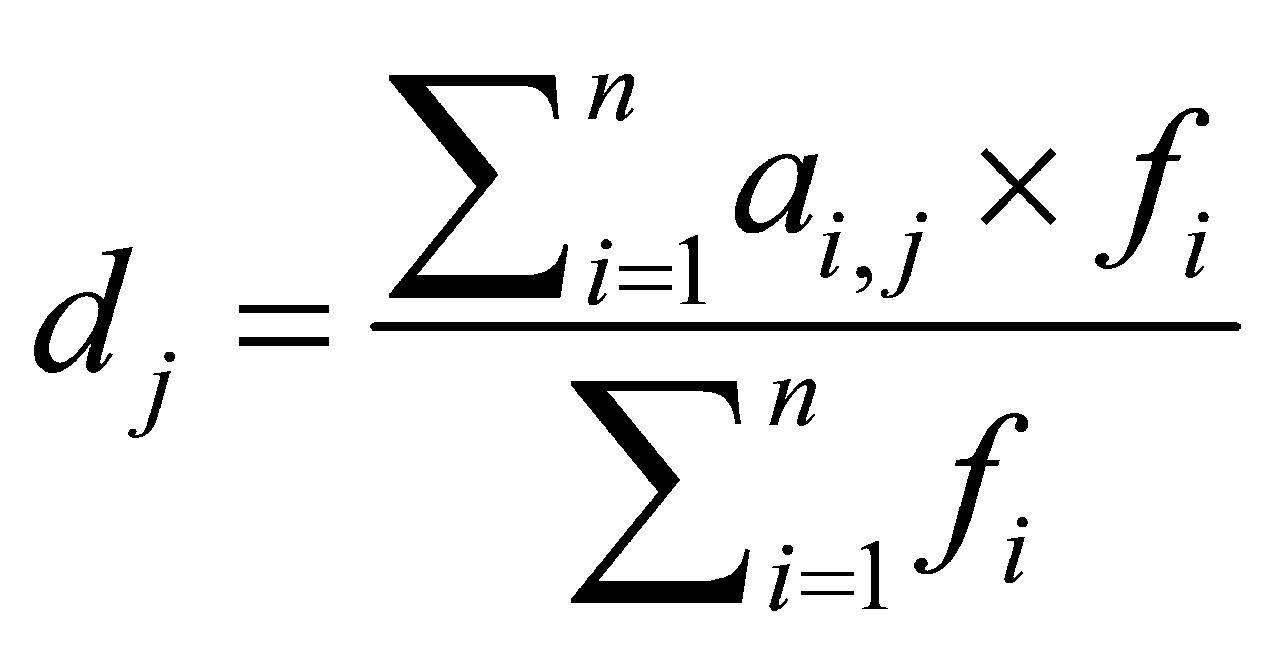 (13)
(13)
(5)两种筛选结果的比较
加权法综合考虑了所有数据的稳定程度,而叠加法对每一个单独数据的稳定性程度设定了门槛,如果只考察6点吃水值的变化程度,二者差别不大,但是在引入纵横倾数据后,情况就不同了。因为纵横倾值是相对两侧吃水值相减的结果,所以其变化量相对于单侧吃水值的变化量是翻倍的,从曲线上就能看出二者的变化并不同步。因此,本研究引入加权法,综合反映整体稳定性大小,得到的是11个维度上稳定性最高的数据集。另外,由于波浪变化受各种环境影响,如风力、风向、岸边、船身、涌浪及水上漂浮物等,尤其是小波浪的破碎造成的短时间内水位快速变化会造成异常吃水值的出现。因此,本研究引入叠加法,利用其对单点高变异性的零容忍度,有效剔除了单点稳定性较差的数据集。所以两种方式得到的数据有重叠部分和差异部分,如图9和图10所示。其中,实线框内为加权法筛选出的数据区域,虚线框内为叠加法筛选出的数据区域,区域1和3中虽然6点吃水较平稳,但纵横倾出现了较大变化,所以叠加法剔除了,而加权后的总体稳定性变化不大,所以加权法采用了这部分数据;区域4中6点水尺和纵横倾都略有波动,加权后的结果变化较大,故被加权法抛弃,而叠加法可以接收;区域2和5为两种算法重叠部分,属于既没有异常值的出现,又满足整体稳定性最佳的区域。因此,本研究给出两种筛选结果,供检验人员根据现场情况参考使用,推荐采用重叠部分。
2 系统测试和评价
为考察系统应用效果,对本套水尺计重测量设备及算法在南京港务(集团)新生圩港务分公司散货装卸码头401泊位进行了应用测试,同时安排传统人工测量对照组进行比对,测量条件及结果见表3。与人工观测相比,总体偏差小于0.5%,符合现有水尺计重标准的要求[16]。
之后又进行了10次测量比对试验,总结了人工观测结果与自动测量结果的平均相对差对比情况,具体结果见表4,变化趋势如图11所示。
表4 人工观测结果与自动测量结果的相对差对比
Table 4 Comparison of the relative difference between automatic measurements and manual measurements
序号 | 比对结果 | ||
前尺相对差 (%) | 后尺相对差 (%) | 前后差相对差 (%) | |
1 | 0.07 | 0.144 | 0.049 |
2 | 0.088 | 0.168 | 0.072 |
3 | 0.138 | 0.161 | 0.085 |
4 | 0.155 | 0.147 | 0.102 |
5 | 0.082 | 0.050 | 0.047 |
6 | 0.119 | 0.170 | 0.054 |
7 | 0.133 | 0.146 | 0.053 |
8 | 0.146 | 0.158 | 0.097 |
9 | 0.082 | 0.026 | 0.035 |
10 | 0.187 | 0.181 | 0.116 |
平均 | 0.120 | 0.135 | 0.071 |
从图11中可以看出,不论前尺或后尺,人工观测结果与自动测量结果的相对差平均值都在0.2%以内,前后尺相减后的相对差平均值则明显更小,主要原因是前后尺相减抵消了船身水尺刻度不准或船体变形造成的误差,总体平均的结果控制在0.1%以内,大大优于标准所规定的相对误差范围。
3 结论
本研究利用便携式电磁波雷达和激光测距仪设计了全新的船舶水尺测量装置,开发了新的吃水深度值测量计算方法。采用远距离无线通信技术和实验室虚拟仪器工程平台实现了6部水尺测量装置实时远程通信和控制,实现了水尺计重过程中测量值的长时间、全方位、全自动同步采集。一系列测试过程及结果分析证实,本研究提出的智能水尺测量系统及算法在科学性和准确性上相较于传统水尺计重测量方法具有显著的优势,主要展现出以下两方面的改进:(1)能够兼容多种不同的甲板和船舷类型,有效解决了艏艉吃水的数字化测量问题。(2)通过采用6点同步测量模式,并结合全新的数据处理方法,有效地解决了传统人工测量和机器视觉测量中难以避免的多点数据瞬时一致性问题,显著提升了测量的准确度。
参考文献
[1] 朱景林, 朱金善. 基于误差传递原理的水尺计重误差分析[J]. 计量学报, 2021, 42(5): 609-614.
[2] 邓国风, 李洪星. 进口大宗法检商品水尺计重短重风险分析及应对措施[J]. 中国海关, 2023(1): 86-87.
[3] 叶晓同. 基于超声相控阵的新型船舶计重技术研究[D]. 杭州: 中国计量大学, 2022.
[4] 张方, 胡明豪, 林航, 等. 船舶水尺计重误差分析[J]. 中国水运, 2020(4): 81-82.
[5] 黄彪斌, 赖华海, 周立群, 等. 无人机在水尺计重领域的应用[J]. 中国水运, 2020(12): 77-79.
[6] 王猛, 刘进涛, 刘冲伟, 等. 无线图传技术无人机在大宗商品水尺计重中的应用[J]. 中国口岸科学技术, 2022, 4(7): 25-29.
[7] 张忠义, 马赛男, 丁海涛, 等. 一种新型水尺计重无人船平台系统的设计及应用探索[J]. 中国口岸科学技术, 2024, 6(2): 15-19.
[8] 沈益骏, 陈林, 刘冲伟, 等. 一种船舶水尺计重用机器人的研制和应用[J]. 船海工程, 2023, 52(5): 64-68.
[9] 周广程. 图象处理技术在船舶吃水自动检测系统中的应用[D]. 南京: 南京理工大学, 2006.
[10] 刘丹. 基于图像处理的散货船港航交重计量系统[D]. 大连: 大连海事大学, 2012.
[11] 沈益骏, 李博, 王鹏皓. 雷达液位计测距技术在船舶水尺计重中的应用[J]. 中国舰船研究, 2017, 12(6): 134-140.
[12] 王安. 基于LoRa通讯的路灯光感开关设计[J]. 信息工程, 2022, 30(11): 47-50+42.
[13] 王鹏皓, 李博, 闫雨, 等. 一种利用雷达液位技术测量船舶水尺的方法[J]. 中国水运(下半月), 2017, 17(9): 18-20+23.
[14] 牛长喜, 王西超, 谭宏武. 距离—角度法水位观测探索与研究[J]. 中国水利, 2004(5): 52-53+5.
[15] 沈嘉炜. 波浪作用下双船干涉的数值模拟[D]. 哈尔滨: 哈尔滨工业大学, 2021.
[16] SN/T 3023.2—2021进出口商品重量鉴定规程 第2部分: 水尺计重[S]. 北京: 中国标准出版社, 2021.
基金项目:南京海关科研项目(2022KJ43)
第一作者:吴璟(1975—),男,汉族,北京人,硕士,高级工程师,主要从事进出口商品检验鉴定及国际航运货船运载重量快速鉴定技术和装备研发等工作,E-mail: jimwright@126.com
通信作者:唐晨(1988—),男,汉族,江苏扬中人,硕士,工程师,主要从事进出口商品检验鉴定及国际航运货船运载重量快速鉴定技术和装备研发等工作,E-mail: tangchen8862@163.com
1. 南京海关工业产品检测中心 南京 210019
2. 沈阳海关技术中心 沈阳 110067
1. Nanjing Customs Industrial Products Testing Center, Nanjing 210019
2. Shenyang Customs Technical Center, Shenyang 110067

图4 控制和采集软件
Fig.4 Control and acquisition software
表1 数据系列对应关系表
Table 1 Comparison chart of data series
序号j | 位置说明 |
1 | 艏左 |
2 | 舯左 |
3 | 艉左 |
4 | 艏右 |
5 | 舯右 |
6 | 艉右 |
7 | 艏横倾 |
8 | 舯横倾 |
9 | 艉横倾 |
10 | 左纵倾 |
11 | 右纵倾 |

图6 激光测距示意图
Fig.6 Schematic diagram of laser ranging
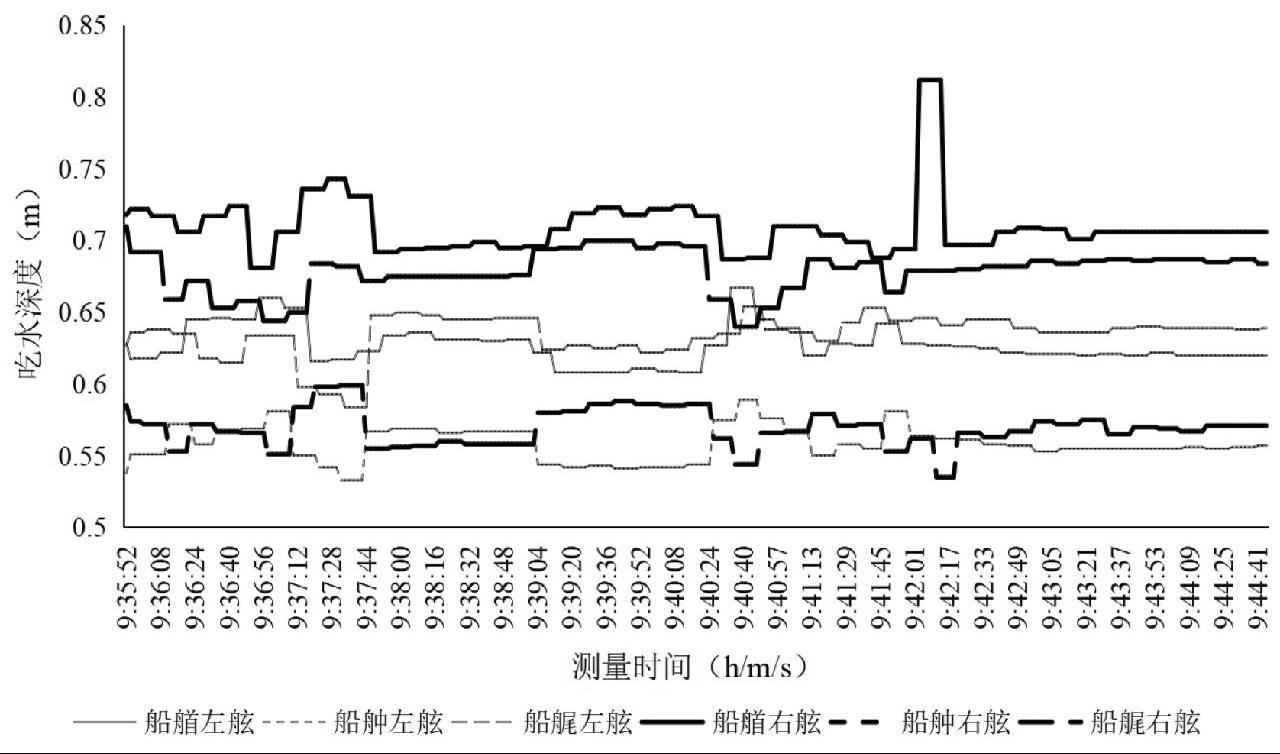
图7 6点吃水高度曲线图
Fig.7 Draft graph of six points
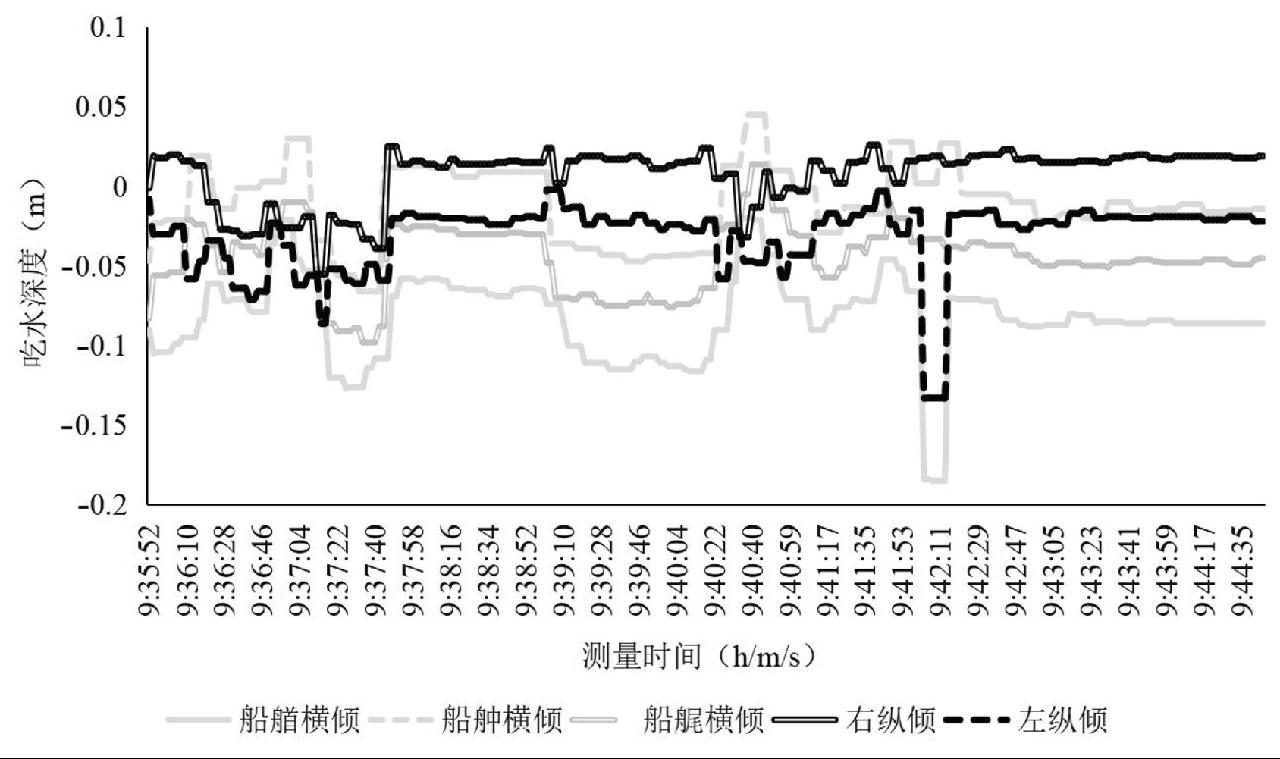
图8 纵横倾曲线图
Fig.8 Graph of trims and heels

图9 6点吃水值取值区间示意图
Fig.9 Schematic diagram of the range of drafts at six points
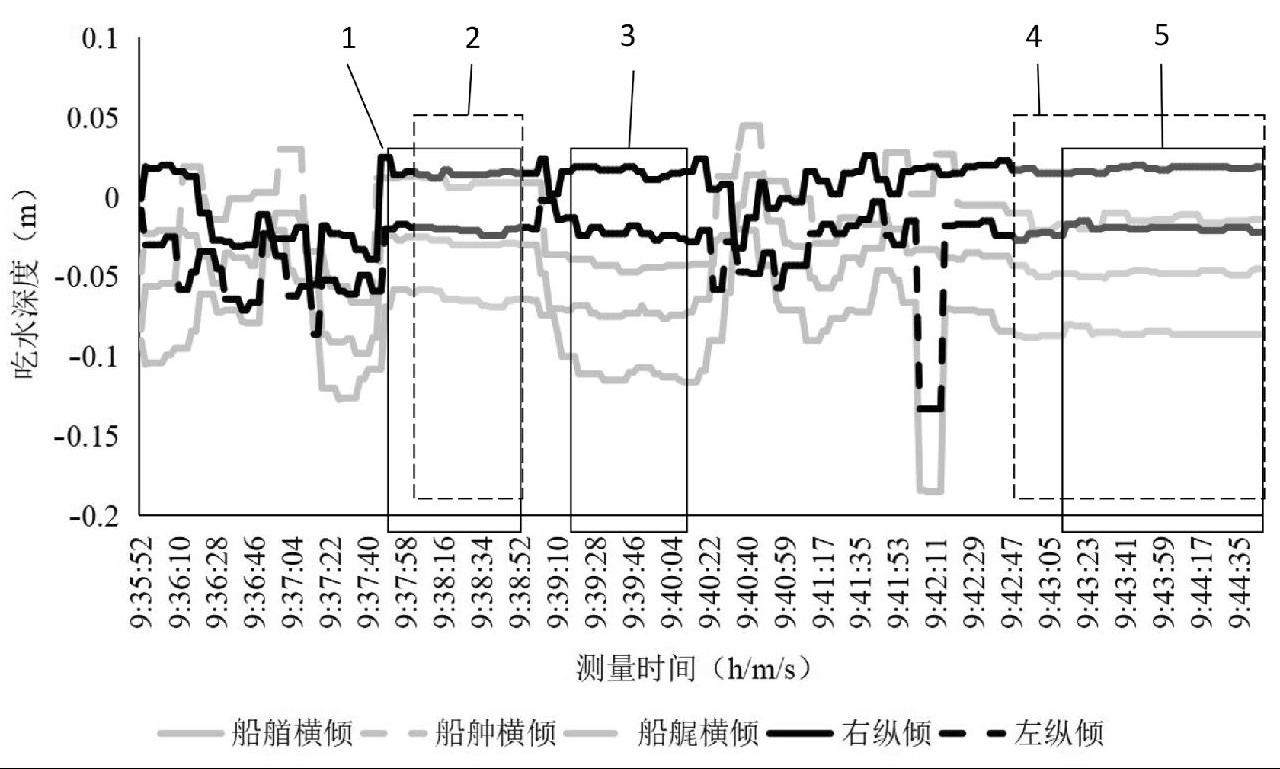
图10 纵横倾取值区间示意图
Fig.10 Schematic diagram of the range of trims and heels
表3 自动测量与人工观测的结果比对
Table 3 Comparison of automatic measurements with manual measurements
前后尺 | 测量点位置 | 人工观测值 (m) | 自动测量值 (m) | 绝对差 (m) | 相对差 (%) | 平均相对差 (取绝对值) (%) |
前尺 | 艏左 | 9.93 | 9.932 | 0.002 | 0.023 | 0.070 |
艏右 | 9.88 | 9.871 | -0.009 | -0.086 | ||
舯左 | 10.43 | 10.428 | -0.002 | -0.017 | ||
舯右 | 10.39 | 10.394 | 0.004 | 0.034 | ||
艉左 | 10.81 | 10.795 | -0.015 | -0.141 | ||
艉右 | 10.79 | 10.803 | 0.013 | 0.117 | ||
后尺 | 艏左 | 4.28 | 4.273 | -0.007 | -0.166 | 0.144 |
艏右 | 4.29 | 4.283 | -0.007 | -0.169 | ||
舯左 | 5.50 | 5.493 | -0.007 | -0.125 | ||
舯右 | 5.54 | 5.537 | -0.003 | -0.051 | ||
艉左 | 6.94 | 6.922 | -0.018 | -0.256 | ||
艉右 | 6.94 | 6.947 | 0.007 | 0.096 | ||
前后尺差 | 艏左 | 5.65 | 5.659 | 0.009 | 0.095 | 0.049 |
艏右 | 5.59 | 5.589 | -0.001 | -0.013 | ||
舯左 | 4.93 | 4.935 | 0.005 | 0.049 | ||
舯右 | 4.85 | 4.856 | 0.006 | 0.061 | ||
艉左 | 3.87 | 3.872 | 0.002 | 0.023 | ||
艉右 | 3.85 | 3.856 | 0.006 | 0.055 |
注: 以上数据是对某大豆船舶进行的现场水尺计重; 天气: 晴; 风量: 2级.
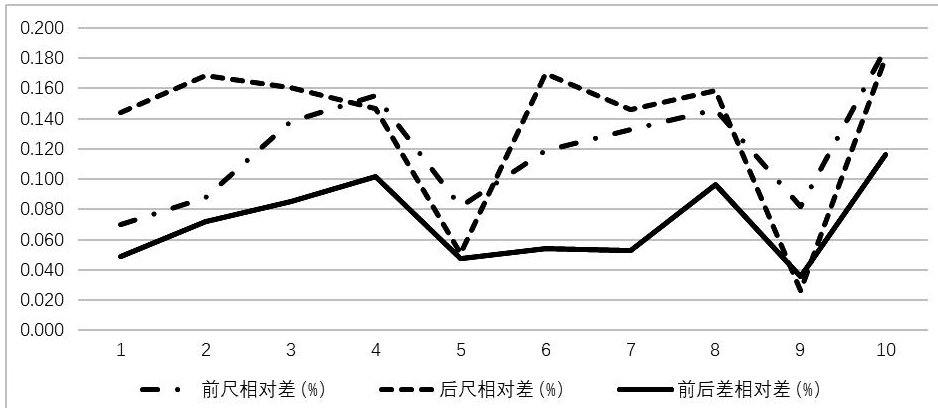
图11 人工观测结果与自动测量结果相对差的对比图
Fig.11 Graph of the relative difference between automatic measurements and manual measurements







