CopyRight 2009-2020 © All Rights Reserved.版权所有: 中国海关未经授权禁止复制或建立镜像
基于SARIMA模型与LSTM神经网络模型的中国肺结核发病预测比较研究
作者:武长礼 徐锋顺 段萌 李海川 罗银波
武长礼 徐锋顺 段萌 李海川 罗银波
武长礼 1 徐锋顺 2 段 萌 2 李海川 2 罗银波 3
摘 要 本研究通过评估季节性自回归差分移动平均模型(Seasonal Autoregressive Integrated Moving Average,SARIMA)与长短期记忆(Long Short-Term Memory,LSTM)神经网络在预测中国肺结核发病的效能差异,为传染病预警系统构建提供模型选择依据。基于2011—2023年全国肺结核监测数据,通过划分训练集与测试集,分别构建SARIMA模型和LSTM神经网络模型,采用绝对百分比误差(Absolute Percentage Error,APE)、平均绝对百分比误差(Mean Absolute Percentage Error,MAPE)和均方根误差(Root Mean Square Error,RMSE)等指标来评价外推预测精度,最后用上述最优参数模型来进行预测分析。结果显示,SARIMA最优模型(1,1,0) (1,1,0)12在预测后期APE较LSTM高,SARIMA模型和LSTM神经网络模型的MAPE分别为11.26%和9.45%,RMSE分别为9791.58和8337.80。结果表明,SARIMA模型和LSTM神经网络模型均能对中国肺结核发病情况进行较好的预测,LSTM神经网络模型在捕捉非线性时序特征方面具有显著优势,尤其适用于中长期预测场景。
关键词 时间序列分析;肺结核监测;模型比较;预测
Comparative Study of SARIMA and LSTM Neural Network Models for Pulmonary Tuberculosis Incidence Prediction in China
WU Chang-Li 1 XU Feng-Shun 2 DUAN Meng 2 LI Hai-Chuan 2 LUO Yin-Bo 3
Abstract This study evaluated the performance differences between the SARIMA and LSTM models in predicting monthly pulmonary tuberculosis incidence in China, providing evidence for infectious disease surveillance system development. Based on the national pulmonary tuberculosis surveillance data from 2011 to 2023, we trained and tested both SARIMA and LSTM models. Predictive accuracy was assessed by Absolute Percentage Error (APE), Root Mean Absolute Percentage Error (MAPE) and Root Mean Square Error (RMSE). The optimal SARIMA model (1,1,0)(1,1,0)12 has a higher APE than the LSTM model in the later stage of prediction. The SARIMA model demonstrated higher MAPE (11.26% vs 9.45%) and RMSE (9791.58 vs 8337.80) compared to the LSTM model. Both models demonstrated satisfactory predictive capabilities, with LSTM exhibiting superior performance in capturing nonlinear temporal patterns, particularly in later prediction phases.
Keywords time series analysis; tuberculosis surveillance; model comparison; prediction
基金项目:武汉海关科研项目(2024WK004)
第一作者:武长礼(1986—),男,汉族,湖北孝感人,硕士,主治医师,主要从事口岸传染病监测与防控研究工作,E-mail: changliw2018@163.com
1. 湖北国际旅行卫生保健中心(武汉海关口岸门诊部) 武汉 430070
2. 武汉海关 武汉 430048
3. 湖北省疾病预防与控制中心 武汉 430070
1. Hubei International Travel Health Care Center (Outpatient Department of Wuhan Customs Port), Wuhan 430070
2. Wuhan Customs, Wuhan 430048
3. Hubei Provincial Center for Disease Control and Prevention, Wuhan 430070
中国口岸科学技术
肺结核属于国家法定乙类传染病,同时也是口岸监测的传染病之一。根据《2024年全球结核病报告》数据显示,2023年全球新发结核病1080万例,发病率为134/10万人,较2022年分别增长0.93%和0.2%[1]。2023年我国肺结核报告发病61.31万例,报告发病率为43.49/10万,近20年来,尽管肺结核发病率呈下降趋势[2],但人口流动加剧和耐药菌株出现给防控工作带来新挑战。
在传染病预测领域,传统统计模型与机器学习方法的预测效能比较是研究热点。季节性自回归差分移动平均模型(Seasonal Autoregressive Integrated Moving Average,SARIMA)通过差分运算消除序列非平稳性,结合季节性参数刻画周期波动特征,该模型已被用于许多流行性疾病的发病趋势预测,如乙肝、猩红热、季节性流感、流行性腮腺炎以及布鲁氏-7]。而长短期记忆(Long Short-Term Memory,LSTM)神经网络模型运用记忆单元和门控机制,可有效处理长期依赖关系,近年来广泛应用于传染病的时间序列分10]。本研究系统比较SARIMA模型与LSTM神经网络模型在中国肺结核发病预测中的差异,通过构建混合精度评估体系,揭示两类模型在不同预测周期的性能特点,为肺结核监测和预警系统的构建提供模型选择依据。
1 资料和方法
1.1 资料来源
本研究从中国疾病预防控制中心官网(http://www.chinacdc.cn/)收集的肺结核月报告发病人数数据,涵盖时间为2010年1月—2023年12月。研究数据包括来自全国31个省、自治区和直辖市的报告发病人数,并多次核对数据,以确保其准确性和一致性。
此外,本研究在收集数据期间,中国疾病预防控制中心发布的最新监测数据时间截至2024年10月,而本研究采用SARIMA模型的季节周期为12个月,综合考虑数据周期完整性,故选取截至2023年12月的数据纳入研究。
1.2 方法
1.2.1 SARIMA模型
SARIMA是由季节效应、长期趋势效应、周期性变化和随机干扰组成的时间序列分析中的经典模型。一般来说,时间序列建模方法包括以下四步:
(1)序列平稳化。通过增强迪基-福勒检验(Augmented Dickey-Fuller,ADF)单位根检验评估序列平稳性,当检验统计量对应的p<0.05时拒绝原假设,判定序列平稳;反之则需进行平稳化处理。同时,结合自相关函数与偏自相关函数的衰减特征进行验证:平稳序列表现为均值稳定且波动范围恒定,若存在趋势或周期性波动则需要对原始数据进行对数或者平方根变化、差分处理,直至序列平12]。
(2)模型选择和参数估计。基于平稳序列的自相关图和偏自相关图截尾特性确定非季节项(p,d,q)与季节项(P,D,Q)s参数候选集。其中,季节周期s依据数据采集间隔确定为固定值(月数据s = 12)。采用网格搜索法遍历参数组合,以最小化赤池信息准则为优化目标筛选最优模型。参数估计采用最大似然估计法,确保参数估计量的渐进13]。为筛选出最优模型,以赤池信息准则(Akaike Information Criterion,AIC)作为评估指标,所对应的最小值作为确定最优模型的依据 。
(3)残差诊断与模型验证。通过Ljung-Box Q检验评估残差序列的自相关性,当检验p>0.05时接受残差为白噪声的原假设,表明模型已充分提取时14]。
(4)预测分析及效能评价。将数据分为训练集(2011年1月—2020年12月报告数据)和测试集(2021年1月—2023年12月的报告数据),用上述最优模型进行预测,并对模型进行评价。
1.2.2 LSTM神经网络
LSTM神经网络模型包含一种作为记忆形式的细胞状态,涉及3种关键门结构:分别为负责控制上一时刻信息保留程度的遗忘门、管控当前输入信息进入状态的输入门,以及决定输出信息内容的输出门。它能够通过门控机制向单元状态添加或删除信息。对于当前输入xt和来自前一步的历史信息ht-1,遗忘门ft将输入和先前激活值进行组合,然后经一个非线性sigmoid函数(输出值范围为0—1)传递,以过滤出哪些值要存储,哪些值要忘记或删除,用σ表示。另一方面,输入门 it决定应该在单元状态中存储(记住)哪些信息。sigmoid层决定要更新的值,而tanh层对这些值进行加权,以添加到状态 。通过结合遗忘门所产生的控制信号与输入门生成的新信息,对上一时刻的细胞状态Ct-1进行修正与更新,从而得到当前时刻的新细胞状态
。通过结合遗忘门所产生的控制信号与输入门生成的新信息,对上一时刻的细胞状态Ct-1进行修正与更新,从而得到当前时刻的新细胞状态 。输出门是体系结构中的最后一个门,它决定应该给出哪个作为输出。这个门也有一个用于选择的sigmoid层和一个用于产生最终输出的ta16]。对应方程为公式(1)—公式(6)。
。输出门是体系结构中的最后一个门,它决定应该给出哪个作为输出。这个门也有一个用于选择的sigmoid层和一个用于产生最终输出的ta16]。对应方程为公式(1)—公式(6)。
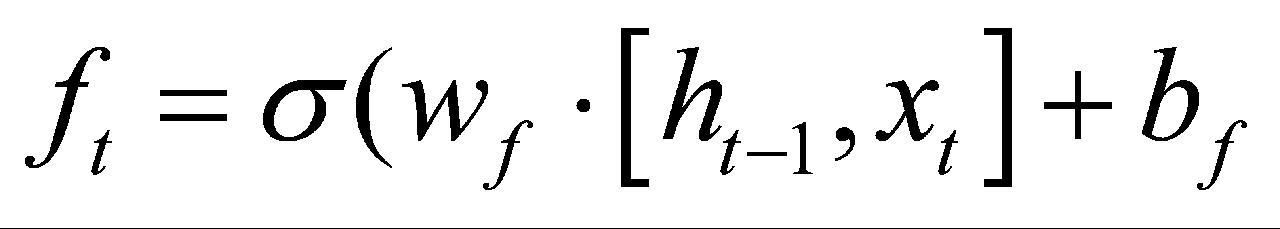 (1)
(1)
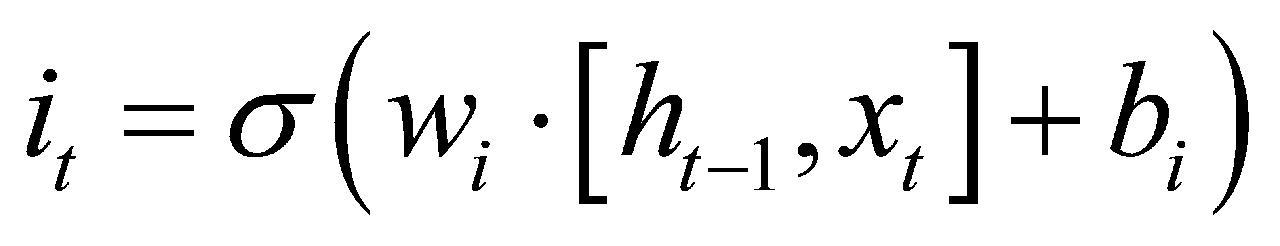 (2)
(2)
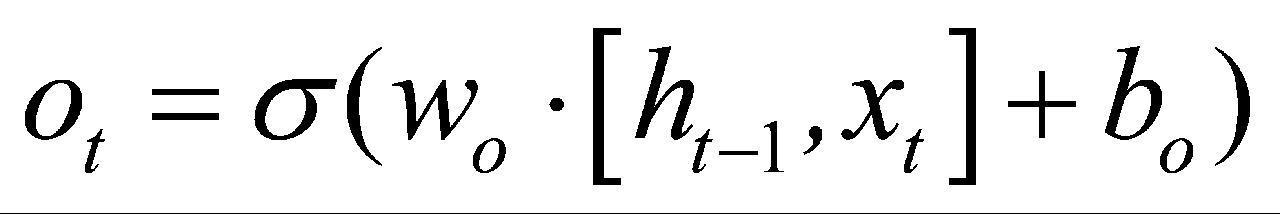 (3)
(3)
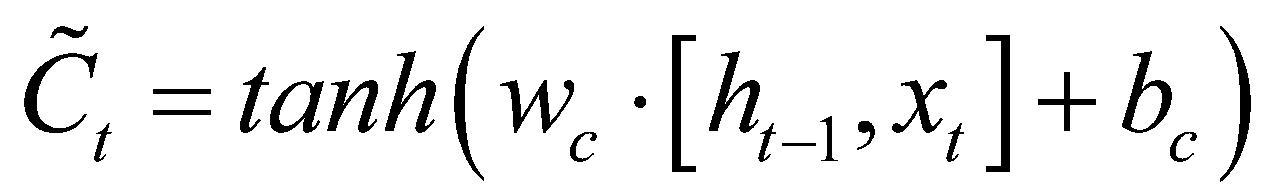 (4)
(4)
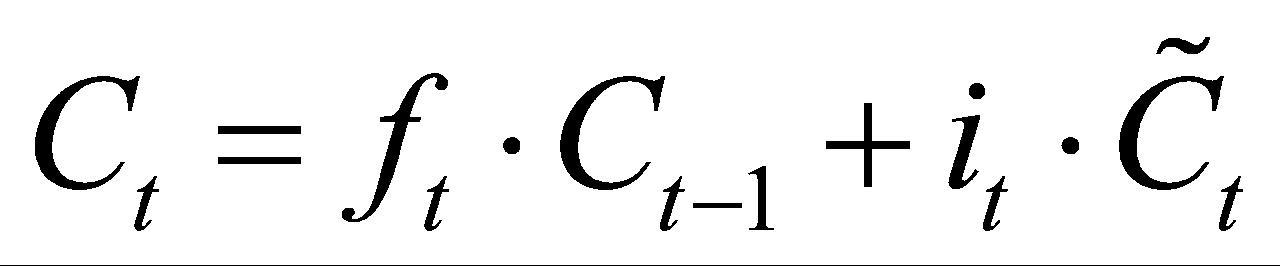 (5)
(5)
 (6)
(6)
式(1)—式(6)中,xt表示当前时间步的输入,ht-1表示前一个时间步的隐藏状态, 表示候选细胞状态,ft、
表示候选细胞状态,ft、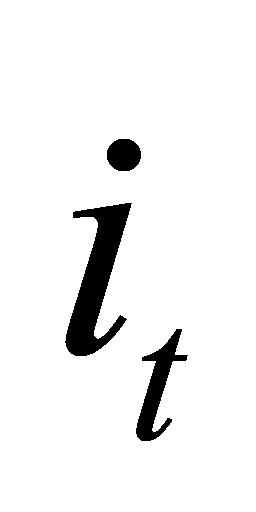 、
、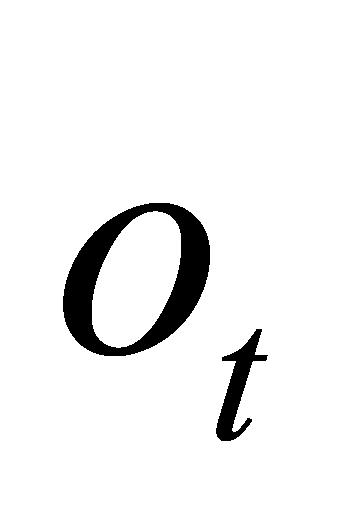 分别表示遗忘门、输入门和输出门,wf、wi和wo表示遗忘门、输入门和输出门权重,
分别表示遗忘门、输入门和输出门,wf、wi和wo表示遗忘门、输入门和输出门权重,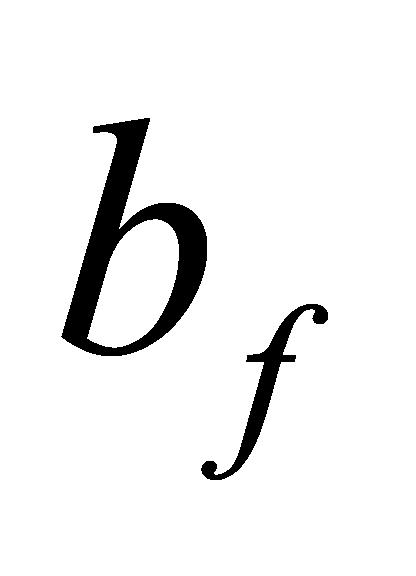 、
、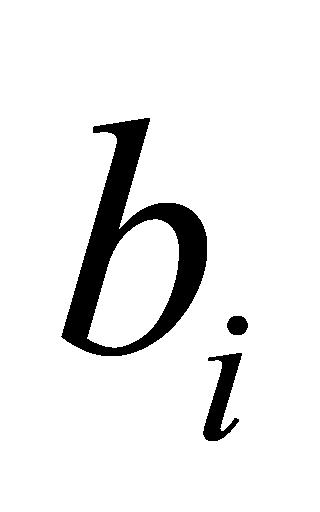 、
、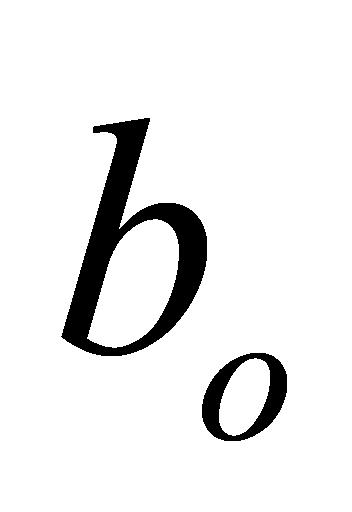 、
、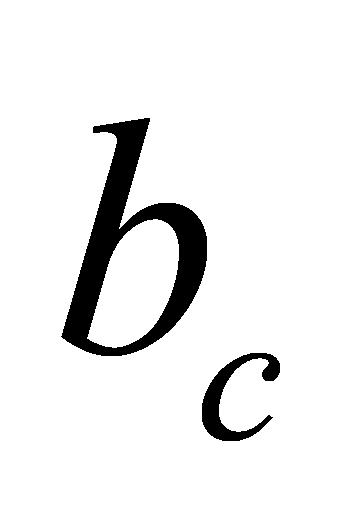 表示遗忘门、输入门偏置、输出门偏置和候选细胞状态的偏置。
表示遗忘门、输入门偏置、输出门偏置和候选细胞状态的偏置。
1.2.3 模型性能评价
采用绝对百分比误差(Absolute Percentage Error,APE)直观反映每个数据点的误差大小,APE越小,预测数据点与观测实际数据点的值越接近;运用平均绝对百分比误差(Mean Absolute Percentage Error,MAPE)和均方根误差(Root Mean Square Error,RMSE)比较原始数据集和预测数据集之间的差异,这两个指标的值越小,表示预测性能越好,预测17]。MAPE不高于10%,说明预测高度准确;MAPE在10%~20%之间,说明预18]。计算方式见公式(7)—公式(9)。
 (7)
(7)
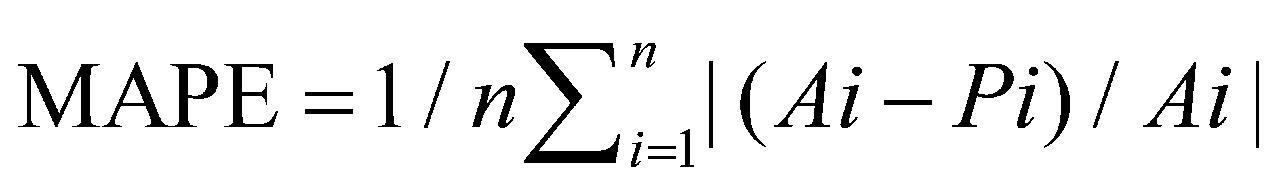 (8)
(8)
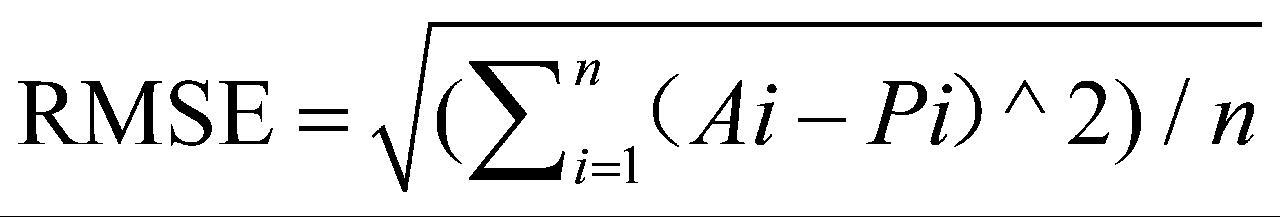 (9)
(9)
式(7)—式(9)中,Ai表示第i个观测数据的真实值,Pi表示第i个观测数据的预测值,n表示观测数据数量。
1.2.4 数据分析处理
采用Excel 2017来整理和录入数据,在R语言(版本:4.4.2)中安装下载arima包进行SARIAM建模;基于Miniconda安装keras所依赖的CPU版本的TensorFlow作为支持后端,配置底层依赖的Python环境(版本:Python 3.9.20)构建深度学习模型;计算结果以p<0.05表示有统计学差异。
2 结果
2.1 肺结核发病趋势
2011—2023年我国共报告肺结核病例1395.5万例,其中,2011年全年报告病例最多,为135.79万例;2022年全年报告病例最低,为71.26万例;2023年全年报告发病病例77.35万例,总体上呈下降趋势,年增长率为-3.06%;整个时期,每年报告发病数的最低月份为2月,报告发病率最多的月份为3月和4月,受到周期性和季节性波动影响。具体图 1所示。
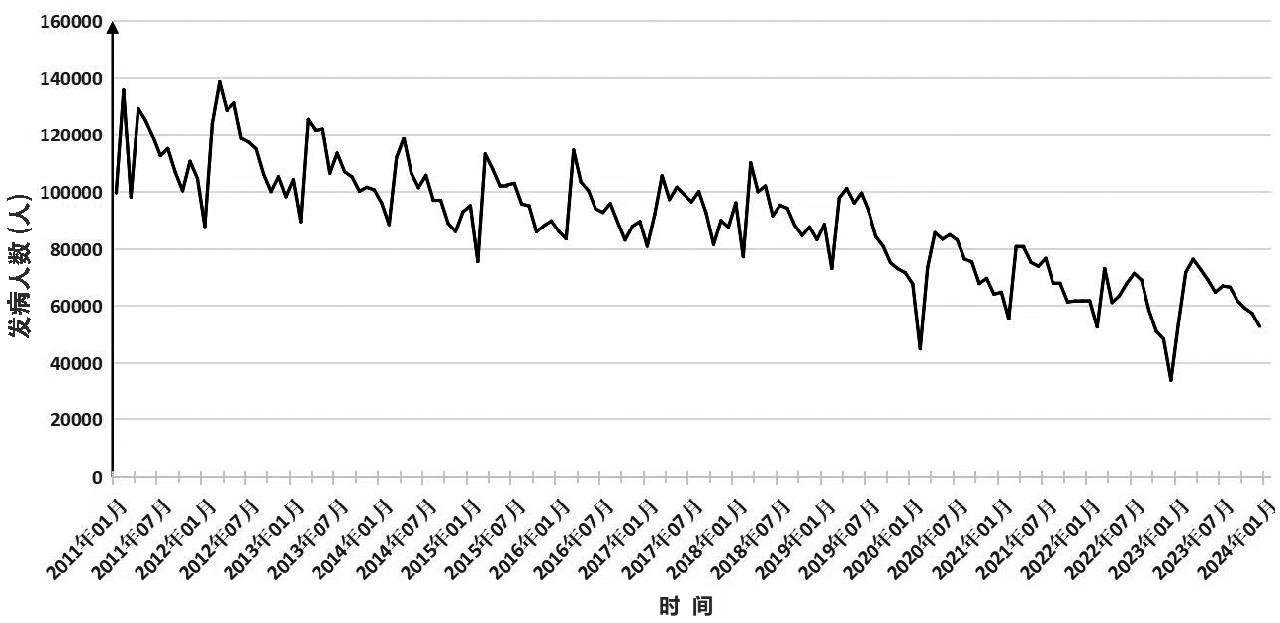
图1 2011—2023年中国肺结核发病人数趋势图
Fig.1 Trend of pulmonary tuberculosis incidence in mainland china from 2011 to 2023
2.2 SARIMA模型结果分析
2011年1月—2020年12月我国肺结核发病例数随时间波动,对原始时间序列趋势进行ADF检验提示t = -1.97,p = 0.59>0.05,提示序列不平稳,经过自然对数转换,一阶差分和季节差分,周期为12,以消除趋势和季节性影响。差分时间序列趋于平稳(t = -7.44,p = 0.01如图2所示。
根据上述序列平稳化的过程可知,差分d = 1,季节性差分D = 1。根据自相关图分析,自相关系数值呈现周期变化,缓慢衰减振荡,初步确定q = 0;根据偏自相关图分析,偏自相关图系数值在1阶出现截尾,初步确定p = 1;根据模型中参数P和Q一般在2以内的原则[19],尝试P和Q依次在0—2从大到小取值;另外,使用auto.arima函数自动生成模型。上述所有的候选SARIMA模型,根据AIC的大小选择最优的SARIMA(1,1,0) (1,1,0)12模型(AIC = -193.0,3和图4所示。
SARIMA(1,1,0) (1,1,0)12采用Ljung-BoxQ检验序列是否存在白色噪声,结果显示:χ2 = 3.76,p = 0.053>0.05,即残差为白色噪声,没有可以提取的有效信息。用该模型进行未来36个月的发病人数预测,结果显示:该模型在前期预测中APE绝大部分在10%以内,少数月份预测的APE有一定的偏差;在2023年全年预测中有9个月预测的APE较大超过10%。
2.3 LSTM神经网络构建
将2011年1月—2020年12月数据作为训练集,其余2020年1月—2023年12月肺结核报告发病人数作为测试集,采用最小-最大标准化的方法对原数据进行归一化处理,使所有数据都在0—1之间,设置时间步长为12,使用Adma 优化算法对参数进行更新,将均一化的发病数据的预测值与实际值的均方误差作为损失函数,采用 tanh作为激活函数,重复地进行 LSTM神经网络训练,需注意是否过拟合的问题和损失函数的变化,最终选取其中表现最佳的参数组合:迭代次数为100次、时间步为12、隐藏层层数为1、隐藏单元为8,学习率为0.0025,然后用得到的LSTM神经网络对肺结核月发病人数进行拟合和预测,直观上看,LSTM神经网络模型和SARIMA模型的预测结果类似,预测的数值大小和变化趋势与实际值差不多,但是在后期预测中,APE较SARIMA模型预测值要小,即LSTM神经网络在远期预测中效果见表 1。
2.4 模型预测结果比较
采用MAPE和RMSE对SARIMA模型和LSTM神经网络模型的模拟性能和预测性能进行比较。在SARIMA模型中,训练集MAPE和RMSE分别为5.62%和8762.47,预测集MAPE和RMSE分别为11.26%和9791.58;在LSTM神经网络中,训练集MAPE和RMSE分别为4.51%和5557.75,预测集MAPE和RMSE分别为9.45%和8337.80。在模型拟合阶段,两种模型对数据的拟合都较好,均在可接受的范围内;但LSTM拟合效果优于SARIMA模型。在预测阶段,两种模型都能较好地预测未来发病趋势。LSTM神经网络模拟处理这类复杂时间序列数据时具有更强的适应性和准确性,尤其在远期预测中表现更优。具体情况如所示。
3 讨论
20世纪90年代,根据世界卫生组织的建议,我国对结核病的防控采取了一系列防控措施,包括根据结核疫情防控形势制定和修订了相关法律法规,为防控工作提供更有力的法律保障;制定和实施结核病防治计划,有利于合理分配医疗资源;提高结核病的监测和防治水平;开展控制结核病国际合作,促进国家间结核病防控技术交流和资源共享,提升公卫体系的整体能力;对人群尤其是学龄前儿童免费接种卡介苗,保护易感高危人群,减少了结核病在人际间的传播;医疗机构对结核病人实施世卫组织推荐的直接督导下短程化疗的治疗方案,减少了结核杆菌耐药发生,提高治愈率;国家实施传染性肺结核免费治疗政策,提高病人依从性,减少了结核病的感染率和死亡率。我国虽然提前5年(即2010年)实现了联合国千年发展目标中关于结核病患病率和死亡率较1990年下降50%的目标,但是在新形势下预防结核病方面仍然面临挑战。因此,科学预测和分析肺结核的发病趋势,对制定肺结核防控策略、优化医疗资源配置、促进公众健康等具有重要意义。
SARIMA模型是经典预测季节时间序列最有效的线性模型之一,通过引入季节性参数,有效捕捉时间序列周期性变化,在处理季节序列线性趋势方面具有一定优势。现实世界中的数据往往蕴含着复杂的非线性关系,这些关系难以用线性函数描述和解释,LSTM神经网络通过调用不同的激活函数来精准地拟合这些复杂的非线性关系,从而高度逼近真实数据的分布规律;同时,LSTM神经网络比传统的“线”性模型更能抵抗干扰,因此当外部因素发生显著变化时,LSTM神经网络仍能做出可靠的预测。
本研究以2010—2023年我国肺结核报告发病人数为基础,采用时间序列分析建立了SARIMA模型和LSTM神经网络模型,分别对肺结核报告发病人数的趋势进行预测和效果评价。在时间序列数据方面,2003年以后我国采取网络直报系统,能够较及时准确地获取报告发病数据,可作为评估肺结核疫情和制定防控策略的重要依据。在模型拟合和预测方面,两者均能较好地拟合肺结核发病趋势和季节性趋势。在模型拟合阶段,两种模型对数据的拟合都较好,均在可接受的范围内;但LSTM拟合效果优于SARIMA模型,说明LSTM神经网络在学习训练数据的规律方面表现更好,能够更准确地捕捉数据中的复杂关系。在模型预测阶段,采用SARIMA最优模型预测肺结核月发病人数时拟合误差在前期较小,远期误差较大;而LSTM神经网络模型拟合效果主要表现在能够持续较好地预测整个时期。主要原因可能是SARIMA模型要求数据(或经过数据变换后的数据)是平稳且为非白噪声序列,在拟合线性关系时具有一定的优势,但是对非线性关系处理能力不足;LSTM神经网络对时间序列数据要求不高,通过引入门控机制,能有效控制信息流动,对重要的长期信息得以保留,无关的短期信息予以过滤,以便更好地捕捉长距离的依赖关系,尤其是非线性关系。
本研究聚焦于2010—2023年我国肺结核月报告发病例数,分析发现肺结核月报告发病人数总体上呈下降态势;运用SARIMA模型和LSTM神经网络模型对肺结核的发病情况进行预测。本研究为决策者合理配置卫生资源以及构建肺结核预警系统提供技术支持。但不容忽视的是,肺结核发病并非单一因素作用的结果,公共卫生政策、人口迁移流动及输入性病例等诸多因素都能对其产生影响。本研究目前仅采用单变量时间序列分析方法,未充分考虑这些复杂因素,致使模型精度仍有提升空间。因此,在未来的研究中可以建立多变量动态预测模型,整合多种影响因素,提升模型的准确性和全面性;构建组合模型,对输入变量组合和参数进行全面优化测试,筛选出最具解释能力的模型,从而实现对肺结核发病趋势的高效、精准模拟,为公共卫生决策提供更有力的科学依据-。
参考文献
[1] World Health Organization. Global tuberculosis report 2024[R]. Geneva: WHO, 2024.
[2]宋媛媛, 李涛, 夏辉, 等. 1997—2023年全国肺结核报告发病流行病学特征[J]. 中国防痨杂志, 2024, 46(10): 1198-1208.
[3] Zhao D, Zhang H, Cao Q, et al. The research of SARIMA model for prediction of hepatitis B in mainland China[J]. Medicine (Baltimore), 2022, 101(23): 1-10.
[4] Wu WW, Li Q, Tian DC, et al. Forecasting the monthly incidence of scarlet fever in Chongqing, China using the SARIMA model[J]. Epidemiology and Infection, 2022, 21, 150: 1-10.
[5] Cong J, Ren M, Xie S, et al. Predicting Seasonal Influenza Based on SARIMA Model, in Mainland China from 2005 to 2018[J]. International Journal of Environmental Research and Public Health, 2019, 16(23): 1-8.
[6] Qiu H, Zhao H, Xiang H, et al. Forecasting the incidence of mumps in Chongqing based on a SARIMA model[J]. BMC Public Health, 2021, 21(1): 1-12.
[7] Cao L, Liu H, Li J, et al. Relationship of meteorological factors and human brucellosis in Hebei Province, China[J]. Science of the Total Environment, 2020, 703: 1-8.
[8]韩天齐, 宋波. 基于LSTM神经网络的麻疹发病率预测[J]. 电脑与电信, 2018(5): 54-57.
[9]陈亿雄, 李苑, 刘小明, 等. 长短记忆神经网络在流行性感冒暴发预测中的应用[J]. 江苏预防医学, 2019, 30(6): 622-625.
[10] Chimmula VKR, Zhang L. Time series forecasting of COVID-19 transmission in Canada using LSTM networks[J]. Chaos Solitons Fractals, 2020, 135: 1-7.
[11] Liu J, Yu F, Song H. Application of SARIMA model in forecasting and analyzing inpatient cases of acute mountain sickness[J]. BMC Public Health, 2023, 23(1): 1-7.
[12]张岳琴, 白丽霞, 光明, 等. 山西省百日咳发病的SARIMA模型预测[J]. 中国卫生统计, 2024, 41(4): 551-554.
[13] Wang Y W, Shen Z Z, Jiang Y. Comparison of ARIMA and GM (1,1) models for prediction of Hepatitis B in China[J]. PLoS ONE, 2018, 13(9): 1-11.
[14] Xia Y, Liao C, Wu D, et al. Dynamic Analysis and Prediction of Food Nitrogen Footprint of Urban and rural residents in Shanghai.International Journal of Environmental[J]. Research and Public Health, 2020, 17(5): 1-13.
[15] Sheikhi F, Kowsari Z. Time series forecasting of COVID-19 infections and deaths in Alpha and Delta variants using LSTM networks[J]. PLoS One, 2023, 18(10): 1-19.
[16] Nabi KN, Tahmid MT, Rafi A, et al. Forecasting COVID-19 cases: A comparative analysis between recurrent and convolutional neural networks[J]. Results in Physics, 2021, 24: 1-14.
[17] Niako N, Melgarejo JD, Maestre GE, et al. Effects of missing data imputation methods on univariate blood pressure time series data analysis and forecasting with ARIMA and LSTM[J]. BMC Medical Research Methodology, 2024, 24(1): 1-32.
[18]胡斌, 卢浩, 刘星言, 等. 基于状态空间的误差–趋势–季节模型在河南省肺结核发病率预测中的应用[J]. 疾病监测, 2022, 37(10): 1349-1355.
[19]王磊, 侯烨, 周美静, 等. 基于R语言的季节性自回归滑动平均(SARIMA)模型对流感样病例发病趋势的预测[J]. 医学动物防制, 2022, 38(4): 349-353.
[20] Xu K, Ding C, Mangan C J, et al. Tuberculosis in China: A longitudinal predictive model of the general population and recommendations for achieving WHO goals[J]. Respirology, 2017, 22(7): 1423-1429.
[21] Wang L, Zhang H, Ruan Y, et al. Tuberculosis prevalence in China, 1990-2010; a longitudinal analysis of national survey data[J]. Lancet, 2014, 383(9934): 2057-2064.
[22] Hu M, Feng Y, Li T, et al. Unbalanced Risk of Pulmonary Tuberculosis in China at the Subnational Scale: Spatiotemporal Analysis[J]. JMIR Public Health and Surveillance, 2022, 8(7): 1-11.
[23] Zhang X, Pang Y, Cui M, et al. Forecasting mortality of road traffic injuries in Chinausing seasonal autoregressive integrated moving average model[J]. Annals of Epidemiology, 2015, 25: 101-106.
[24] Qiao M, Yan S, Tang X, et al. Deep convolutional and LSTM recurrent neural networks for rolling bearing fault diagnosis under strong noises and variable loads[J]. IEEE Access, 2020, 8: 66257-6669.
[25]倪茹玉, 胡婉, 张恒川, 等. ARIMA乘积季节模型与LSTM神经网络模型对我国麻疹发病数预测效果的比较[J]. 现代预防医学, 2023, 50(1): 177-182.
[26]付之鸥, 周扬, 陈诚, 等. 时间序列分析与机器学习方法在预测肺结核发病趋势中的应用[J]. 中国卫生统计, 2020, 37(2): 190-195.
[27]王丹霞, 夏岚, 李婷, 等. 2018—2022年四川省肺结核报告发病数时间序列分析[J].预防医学情报杂志, 2024, 4(40): 349-354+361.
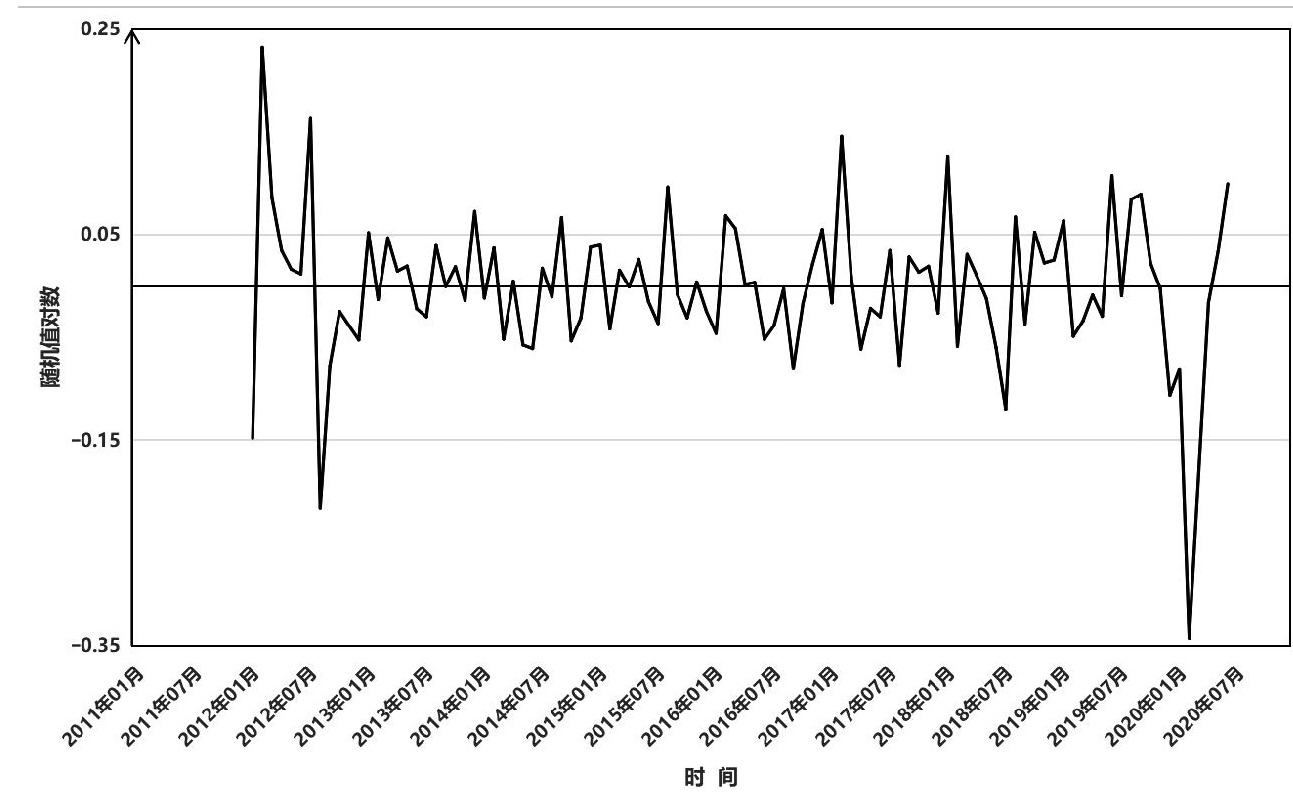
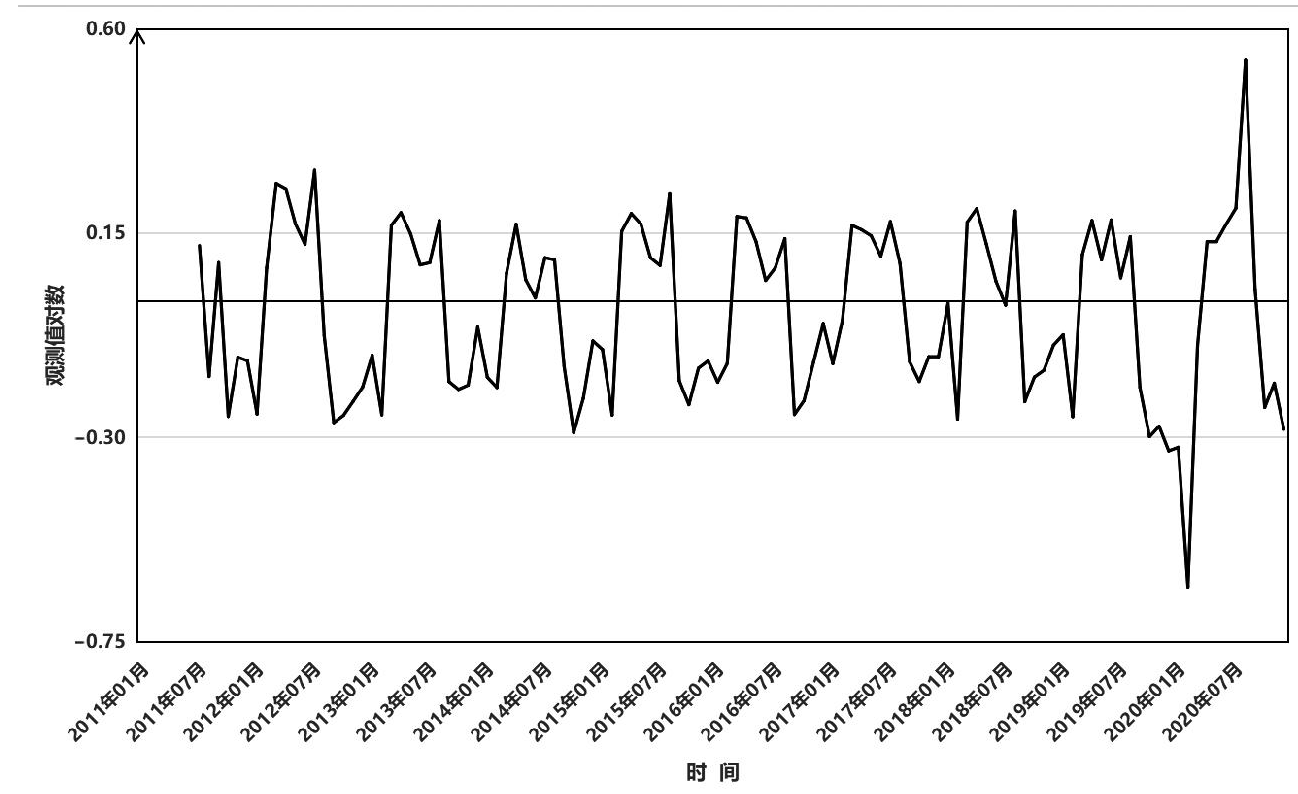
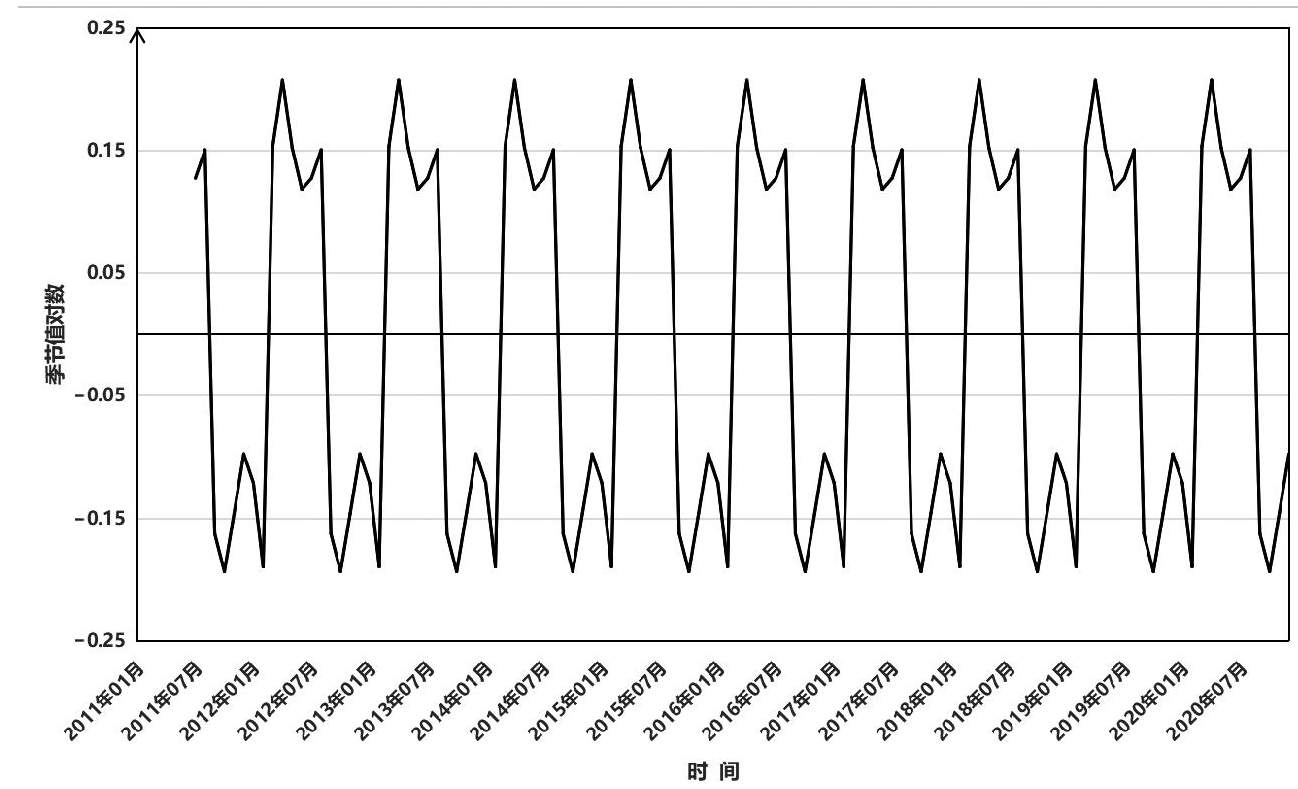
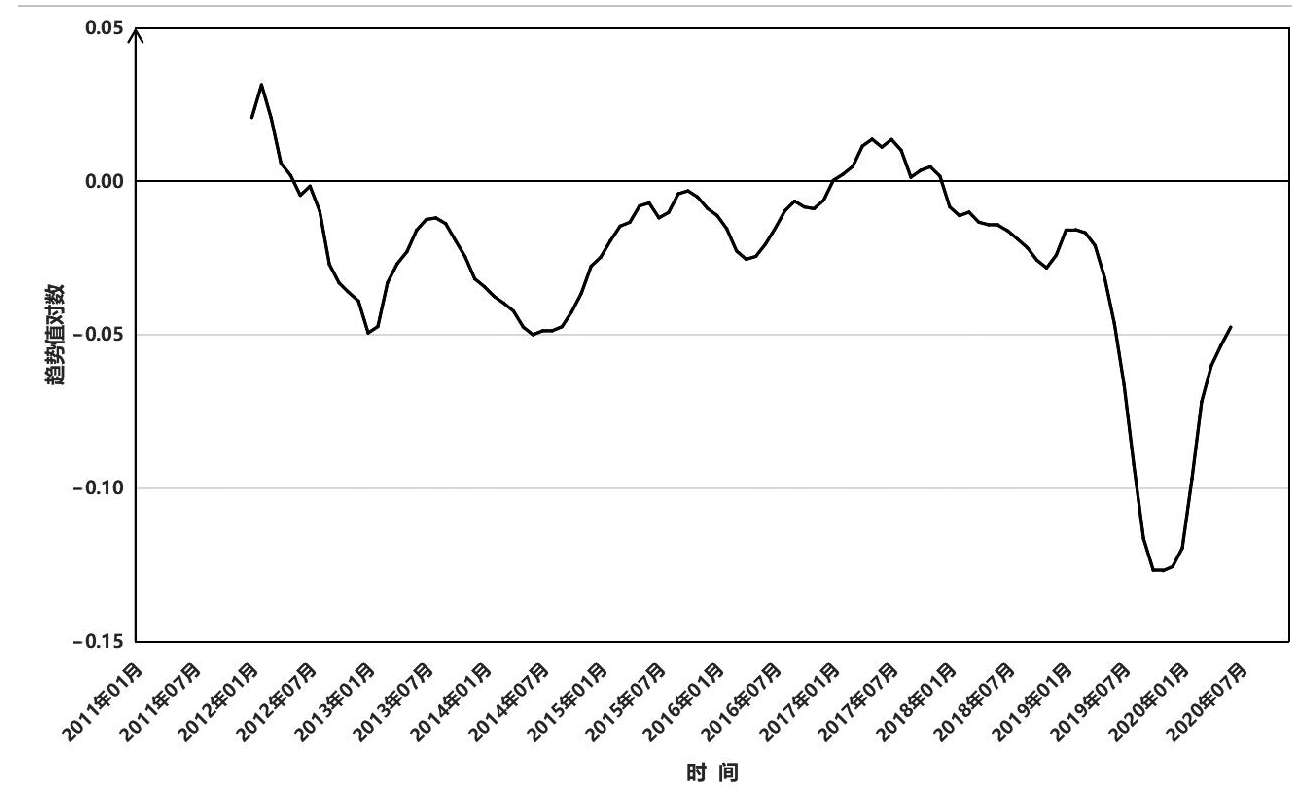
图2 2011—2020年中国肺结核发病人数对数时间分布decompose分解图
Fig.2 Decomposition chart of the logarithm of pulmonary tuberculosis incidence in China from 2011 to 2020
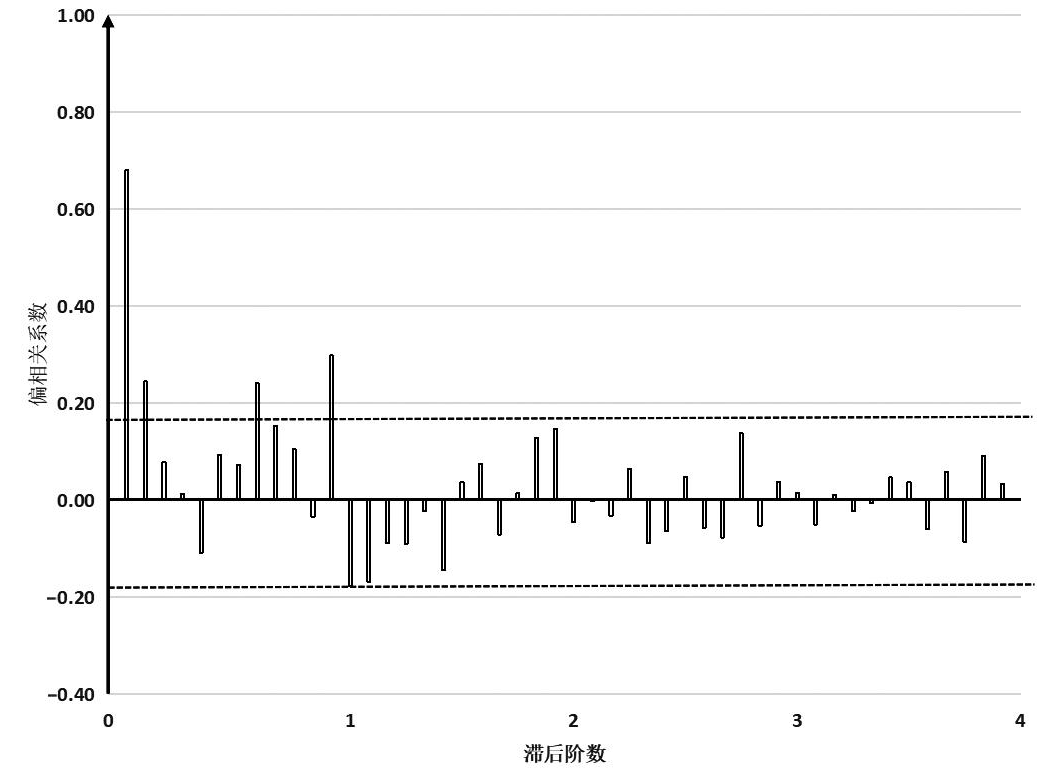
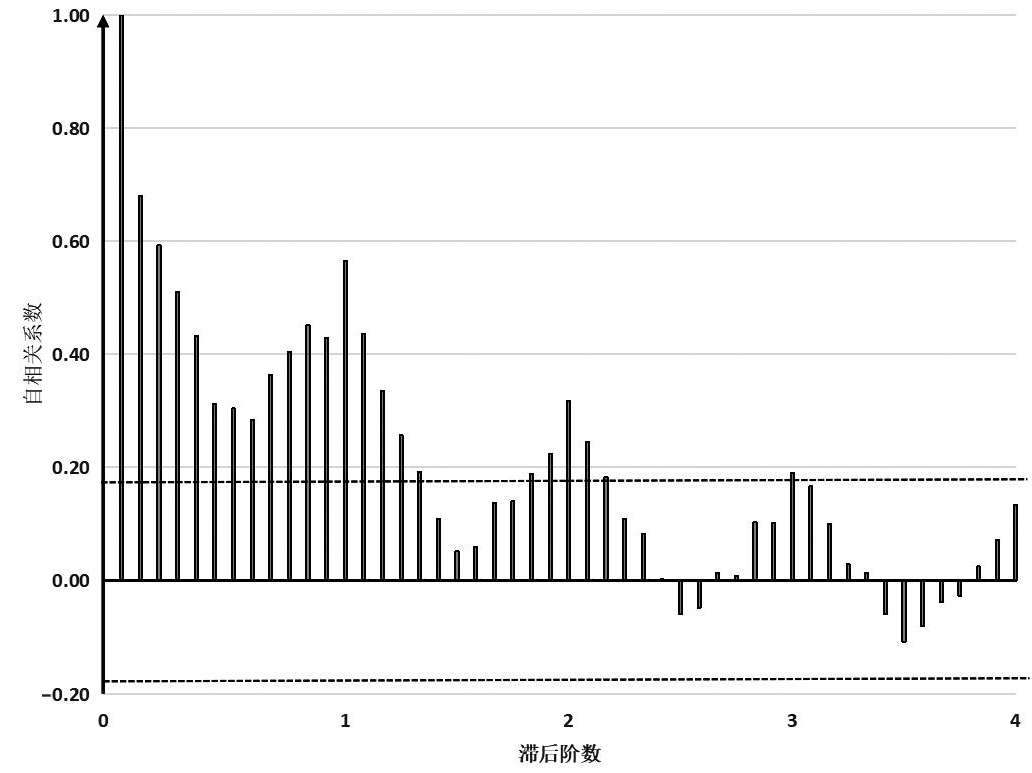
图3 2011—2020年中国肺结核发病人数
对数1阶差分自相关图
Fig.3 Autocorrelogram plot of the first-order differenced logarithmic tuberculosis incidence in China, 2011-2020
图4 2011—2020年中国肺结核发病人数
对数1阶差分偏自相关图
Fig.4 Partial autocorrelation plot of the first-order differenced logarithmic tuberculosis incidence in China, 2011-2020
表1 2011—2020年中国肺结核发病人数实际值和预测值的关系
Table 1 The relationship between the actual and predicted values of the number of pulmonary tuberculosis cases
in China from 2011 to 2020
时间 | 实际值 | SARIMA预测值 | LSTM预测值 | SARIMA APE (%) | LSTM APE (%) |
2021年1月 | 64813 | 64073.84 | 59180.57 | 1.14 | 8.69 |
2021年2月 | 55425 | 43796.74 | 55859.78 | 20.98 | 0.78 |
2021年3月 | 80803 | 69244.46 | 59759.16 | 14.30 | 26.04 |
2021年4月 | 80548 | 78362 | 69931.05 | 2.71 | 13.18 |
2021年5月 | 75243 | 76074.77 | 73641.41 | 1.11 | 2.13 |
2021年6月 | 73884 | 77662.01 | 74452.17 | 5.11 | 0.77 |
2021年7月 | 76648 | 75347.1 | 72499.19 | 1.70 | 5.41 |
2021年8月 | 67966 | 69000.25 | 70772.62 | 1.52 | 4.13 |
2021年9月 | 67812 | 67713.12 | 67871.27 | 0.15 | 0.09 |
2021年10月 | 61391 | 61309.56 | 64439.62 | 0.13 | 4.97 |
2021年11月 | 61753 | 62210.78 | 60902.61 | 0.74 | 1.38 |
2021年12月 | 61788 | 58039.32 | 57268.24 | 6.07 | 7.31 |
2022年1月 | 61697 | 57330.49 | 55637.36 | 7.08 | 9.82 |
2022年2月 | 52596 | 38945.31 | 55830.84 | 25.95 | 6.15 |
2022年3月 | 73110 | 62007.4 | 61664.21 | 15.19 | 15.66 |
2022年4月 | 61185 | 70629.55 | 64355.96 | 15.44 | 5.18 |
2022年5月 | 63590 | 68603.61 | 63760.84 | 7.88 | 0.27 |
2022年6月 | 67901 | 70004.74 | 64040.40 | 3.10 | 5.69 |
2022年7月 | 71422 | 68036.76 | 64835.34 | 4.74 | 9.22 |
2022年8月 | 69019 | 62361.49 | 64408.68 | 9.65 | 6.68 |
2022年9月 | 58638 | 61269.27 | 64536.97 | 4.49 | 10.06 |
2022年10月 | 51125 | 55400.02 | 61502.35 | 8.36 | 20.30 |
2022年11月 | 48352 | 56352.23 | 57919.69 | 16.55 | 19.79 |
2022年12月 | 33951 | 52422.94 | 54405.53 | 54.41 | 60.25 |
2023年1月 | 53730 | 51913.83 | 50036.83 | 3.38 | 6.87 |
2023年2月 | 71841 | 35312.08 | 49805.83 | 50.85 | 30.67 |
2023年3月 | 76331 | 56139.17 | 59051.50 | 26.45 | 22.64 |
2023年4月 | 72846 | 63857.23 | 62982.60 | 12.34 | 13.54 |
2023年5月 | 69068 | 62018.77 | 67682.59 | 10.21 | 2.01 |
2023年6月 | 64788 | 63291.21 | 69966.55 | 2.31 | 7.99 |
2023年7月 | 66989 | 61489.19 | 69434.55 | 8.21 | 3.65 |
2023年8月 | 66563 | 56349.39 | 66963.04 | 15.34 | 0.60 |
2023年9月 | 61859 | 55348.84 | 63654.44 | 10.52 | 2.90 |
2023年10月 | 59239 | 50061.11 | 59990.28 | 15.49 | 1.27 |
2023年11月 | 57432 | 50895.11 | 55954.48 | 11.38 | 2.57 |
2023年12月 | 52826 | 47375.16 | 52025.29 | 10.32 | 1.52 |
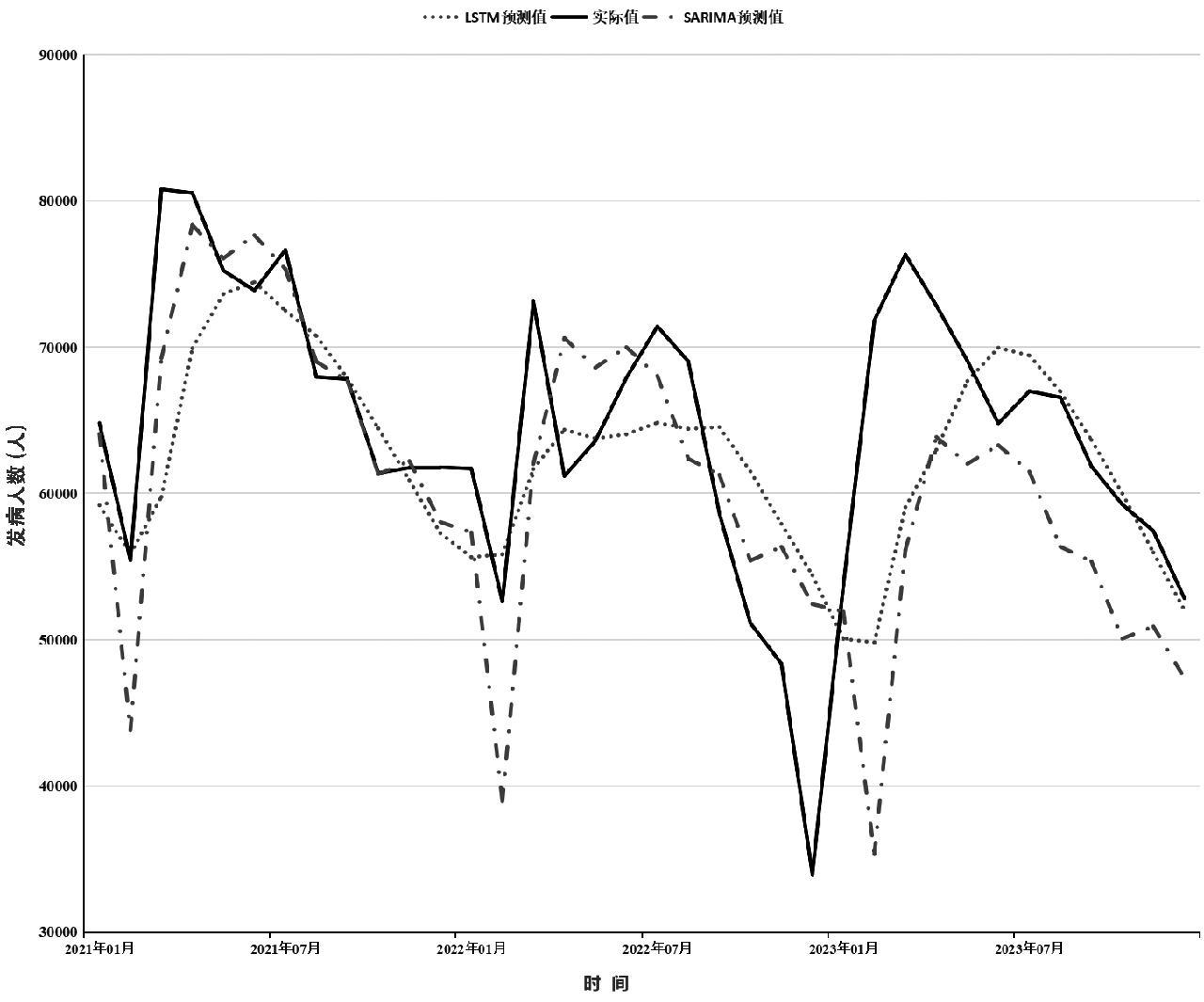
图5 基于SARIMA和LSTM神经网络模型的2021—2023年中国肺结核发病真实情况与预测情况比较图
Fig.5 Comparative analysis of actual and predicted tuberculosis incidence with SARIMA and LSTM neural network modeling approach in China from 2021 to 2023







