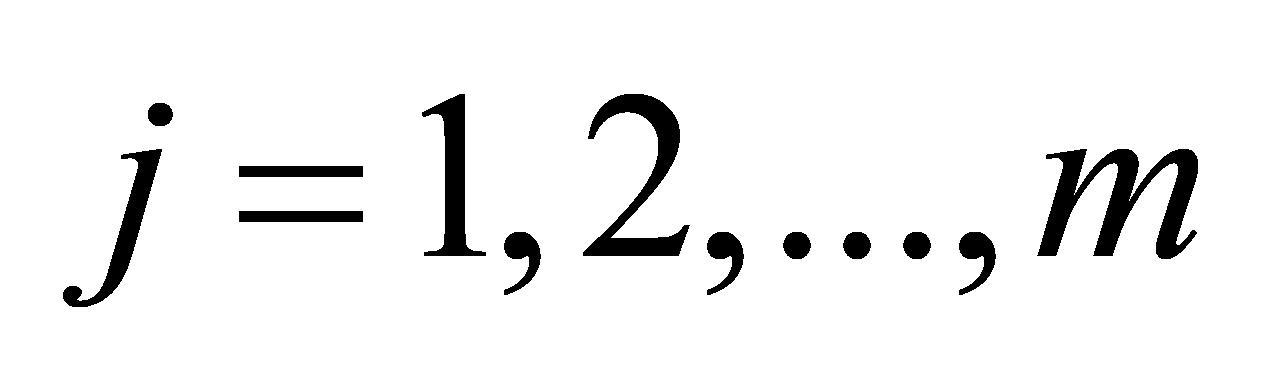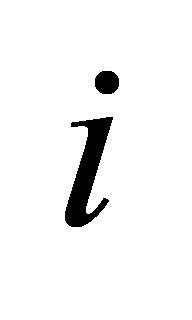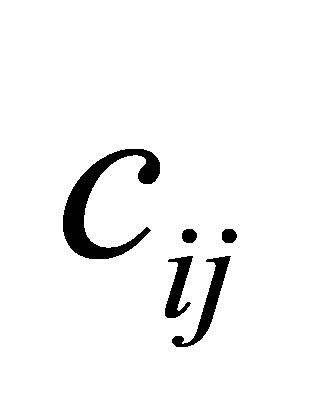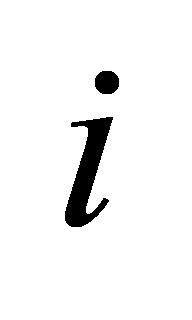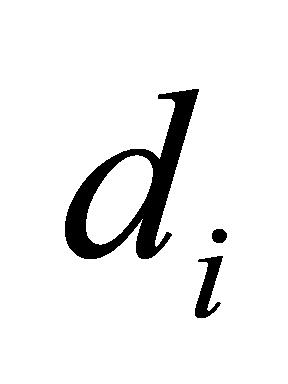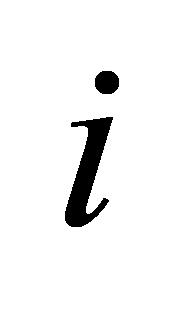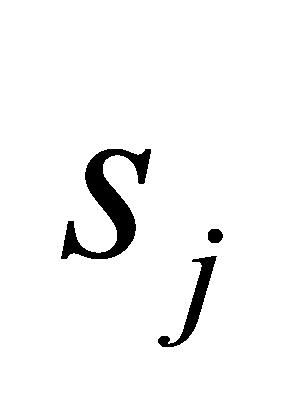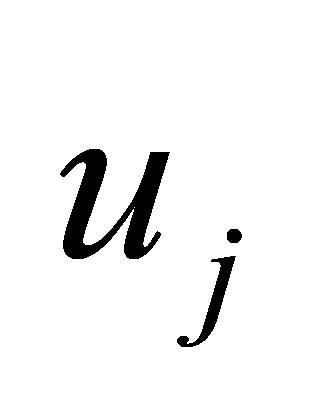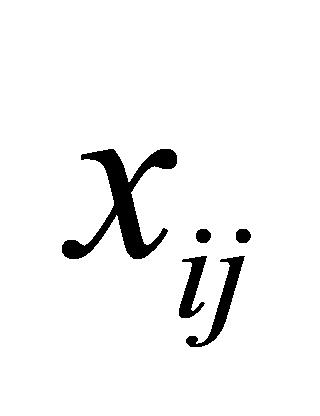CopyRight 2009-2020 © All Rights Reserved.版权所有: 中国海关未经授权禁止复制或建立镜像
仪器设备智能排期模型在数智化实验室管理中的应用研究
作者:张彦彬 冼恩曦 陈江南 苏杨 李嘉敏 纪梓杉 杨熙
张彦彬 冼恩曦 陈江南 苏杨 李嘉敏 纪梓杉 杨熙
摘 要 本研究针对实验室资源约束条件下仪器设备的高效调度问题进行智能排期模型探索。该模型包括以任务完成率、最优完成时间、任务收益、任务成本为目标函数的多目标优化模型及通过极值归一化和加权优劣解距离法(Technique for Order Preference by Similarity to an Ideal Solution,TOPSIS)建立的综合评价模型。采用带精英策略的非支配排序遗传算法(Nondominated Sorting Genetic AlgorithmⅡ,NSGA-Ⅱ)求解多目标优化模型得到最优解。仿真实验中,该模型在同等任务完成度和同等收益的情况下,最优完成时间缩短38.23%,成本降低1.67%。在此基础上,建立动态调度机制,实现已排期的任务再分配,提高设备利用率。这些成果验证了智能排期模型和NSGA-Ⅱ算法的有效性,为其后续实践应用和推广奠定基础。
关键词 智能排期;数智化实验室;仪器设备;多目标优化;非支配排序遗传算法
Equipment Intelligent Scheduling in Digital Intelligent Laboratory Management
ZHANG Yan-Bin1 XIAN En-Xi1 CHEN Jiang-Nan2
SU Yang1* LI Jia-Min1 JI Zi-Shan1 YANG Xi3
Abstract This paper addresses the efficient scheduling of laboratory instruments under resource constraints, investigating an intelligent scheduling model. The model comprises a multi-objective scheduling framework with objective functions focusing on task completion rate, optimal completion time, task benefits, and task costs. Additionally, it includes a comprehensive evaluation model established through extreme normalization and weighted Technique for Order Preference by Similarity to Ideal Solution (TOPSIS). The multi-objective optimization model is solved using the Non-dominated Sorting Genetic Algorithm with an elitist strategy (NSGA-Ⅱ) to obtain the optimal solutions. The example verification results show that the proposed model reduces the optimal completion time by 38.23% and decreases costs by 1.67% under equal task completion rates and benefits. Building on these improvements, a dynamic scheduling mechanism is established to achieve the reassignment of already scheduled tasks, thereby improving equipment utilization.These outcomes validate the effectiveness of the intelligent scheduling model and the NSGA-Ⅱ algorithm, laying a solid foundation for its practical application and promotion.
Keywords intelligent scheduling; digital intelligent laboratory; instruments and equipment; multi-objective optimization; Nondominated Sorting Genetic AlgorithmⅡ(NSGA-Ⅱ)
第一作者:张彦彬(1975—),男,汉族,山东日照人,本科,高级工程师,主要从事信息技术管理工作,E-mail: 13925001898@139.com
通信作者:苏杨(1988—),女,汉族,河南信阳人,硕士,工程师,主要从事信息化测试验证工作,E-mail: 936491750@qq.com
1. 广州海关技术中心 广州 510623
2. 广州海关 广州 510623
3. 广东省科学院测试分析研究所(中国广州分析测试中心) 广州 510623
1. Guangzhou Customs Technology Center, Guangzhou 510623
2. Guangzhou Customs, Guangzhou 510623
3. Guangdong Provincial Key Laboratory of Chemical Measurement and Emergency Test Technology, Guangzhou 510623
随着信息技术的快速发展,创新技术为数智化实验室的建设带来新的机遇和挑战,也为仪器设备管理带来新的思路。如何通过智能化的方式,既能保障检验结果的准确性和高效性,又能实现实验室仪器设备管理的自动化、智能化,提高仪器设备使用效率,实现精细化管理,提升管理质量,是数智化实验室建设的重点之一。
为提高仪器设备的总体使用效率,需要对仪器设备进行整合,使得一些关键设备能够在多个实验项目之间共享。仪器设备整合后,在一个调度周期内,研究采用特定调度算法确定各任务所使用的设备,实现各任务检验顺序的智能排期,合理的智能排期不仅能优化任务分配,确保任务按时高质量完成,还能显著提升设备资源的利用率,避免因排期不合理而导致实验室错失潜在客户群体,进而影响收益水平。
本研究针对实验室资源约束条件下仪器设备的高效调度问题,建立基于多目标优化模型和综合评价模型的智能排期模型,通过非支配排序遗传算法(Nondominated Sorting Genetic AlgorithmⅡ,NSGA-Ⅱ)算法求解,为实验室管理提供一种科学高效的解决方案。智能排期模型如图1所示。
1 多目标优化模型
1.1 模型假设及参数定义设置
假设有n个不同的任务,m个不同的设备,每个任务可用的设备不同,同一个任务在不同设备上检验的时间和成本都不同,每个任务需选择合适的检验设备,确定最优的智能排期方案。在智能排期中应满足以下假设[1]:每个任务只能在1台设备上检验;每一时刻、每台设备只能检验1个任务;一旦任务开始执行,不得中途停止或中断;所有仪器设备在调度开始时均为空闲状态。智能排期模型中的参数设置见表1。
1.2 基于普通任务多目标优化模型
1.2.1 单设备任务排期
假如只有一个任务 ,此时的目标是在满足仪器设备可用性和任务截止日期的条件下,决定是否接受该任务。首先,判断仪器设备是否可用于检验任务。若仪器设备不可用,则不接受该任务,此时任务
,此时的目标是在满足仪器设备可用性和任务截止日期的条件下,决定是否接受该任务。首先,判断仪器设备是否可用于检验任务。若仪器设备不可用,则不接受该任务,此时任务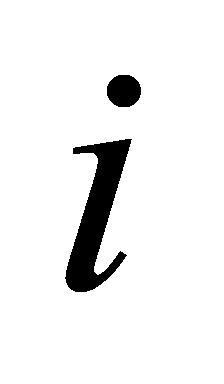 的接受状态设置为0;若仪器设备可用,则继续下一步。其次,判断任务
的接受状态设置为0;若仪器设备可用,则继续下一步。其次,判断任务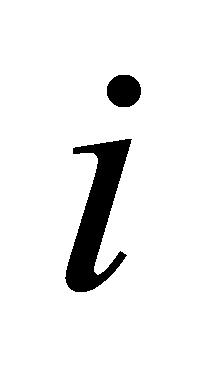 是否被接受。若任务
是否被接受。若任务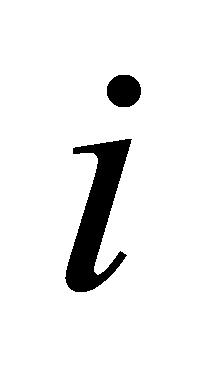 能在规定的截止日期内完成,则接受任务,此时任务
能在规定的截止日期内完成,则接受任务,此时任务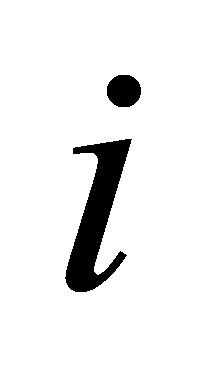 的接受状态设置为1;若任务
的接受状态设置为1;若任务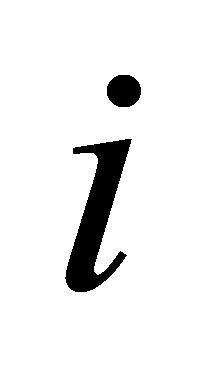 不能在规定的截止日期内完成,则不接受任务,此时任务
不能在规定的截止日期内完成,则不接受任务,此时任务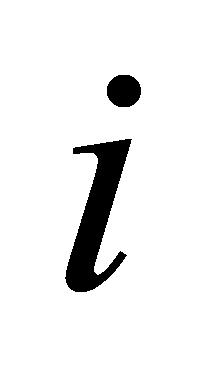 的接受状态设置为0。最后,若任务
的接受状态设置为0。最后,若任务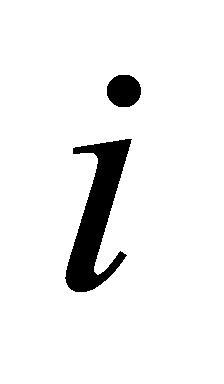 被接受,则更新当前时间和设置仪器设备状态为1。单设备单任务排期流程图如图2所示。
被接受,则更新当前时间和设置仪器设备状态为1。单设备单任务排期流程图如图2所示。
假如此时有多个任务,则只需拓展上述单设备单任务排期模型,对任务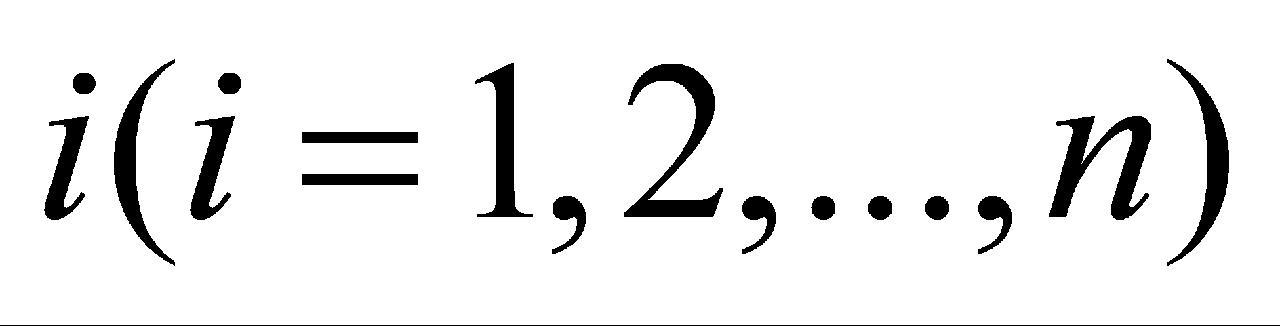 进行遍历,依次判断每个任务是否能被接受。通过这种方式,可以确保在有限的资源和时间限制下,合理地决定是否接受并检验多个任务。
进行遍历,依次判断每个任务是否能被接受。通过这种方式,可以确保在有限的资源和时间限制下,合理地决定是否接受并检验多个任务。
1.2.2 多设备任务排期
当仪器设备数量为m时,需要解决的问题是如何利用有限的仪器设备,在规定的时间内获得较高的净收益并接受较大的任务数,从而实现较优的任务分配。为此,本研究建立了多目标优化模型进行分析。
图2 单设备单任务排期流程图
Fig.2 Single task single device scheduling flowchart
综合考虑任务检验的特点,为均衡分配仪器设备并尽可能满足客户需求,对任务完成率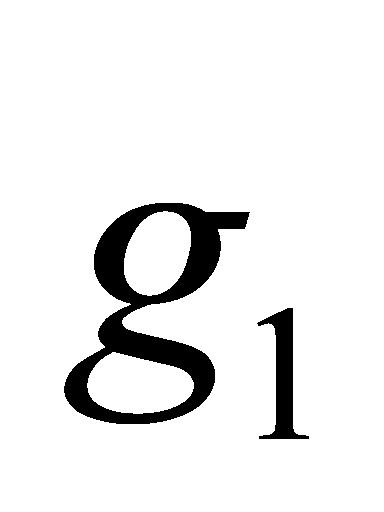 和任务收益
和任务收益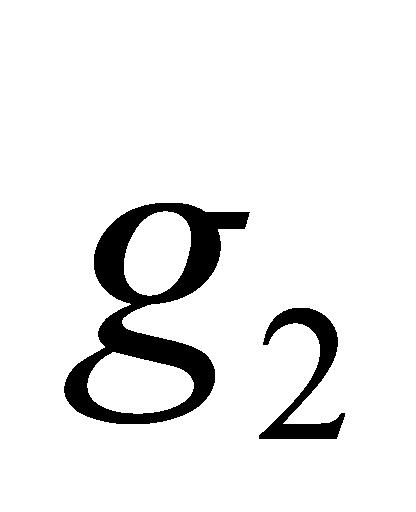 同时取最大且设备最优完成时间
同时取最大且设备最优完成时间 和任务检验成本
和任务检验成本 取最小,建立多目标优化模型,即:
取最小,建立多目标优化模型,即:
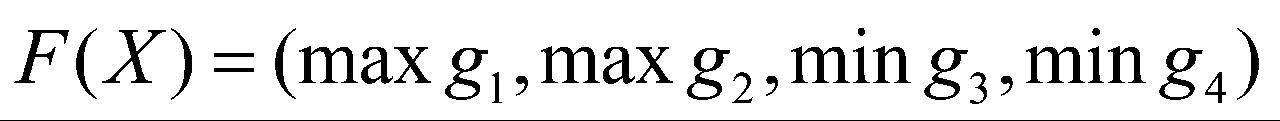 。
。
任务检验应满足结果要求日期,若无法在结果要求日期前提交,则无法接受该任务,进而造成潜在客户的流失。任务完成率是指能接受的任务与总任务的比值[2],按公式(1)计算:
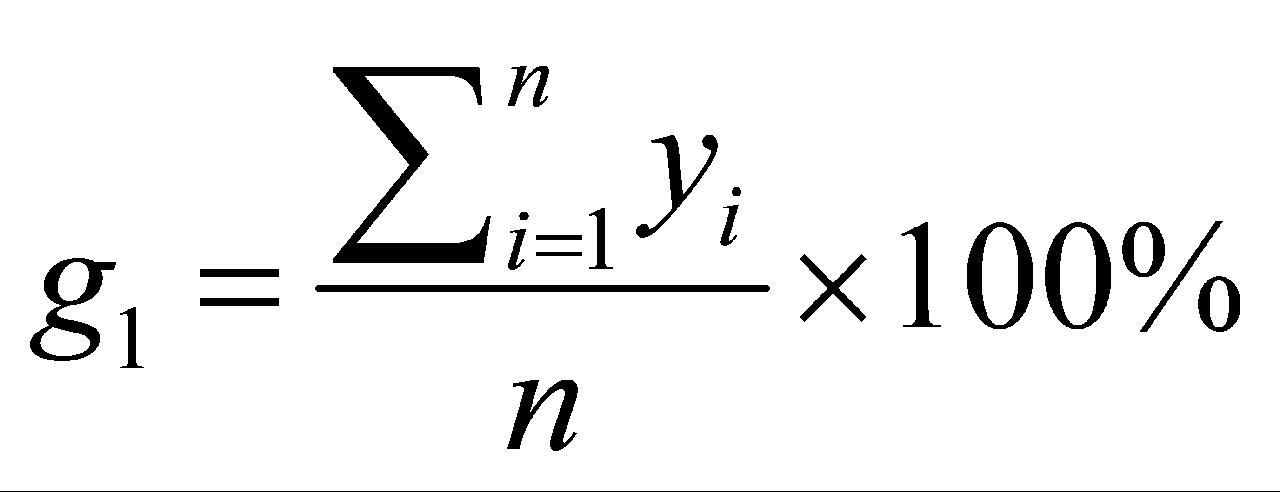 (1)
(1)
在保证任务结果准时提交的前提下,智能排期时应尽可能地提高任务检验的收益。任务检验的收益主要为接受该任务所获得的收益,计算见公式(2):
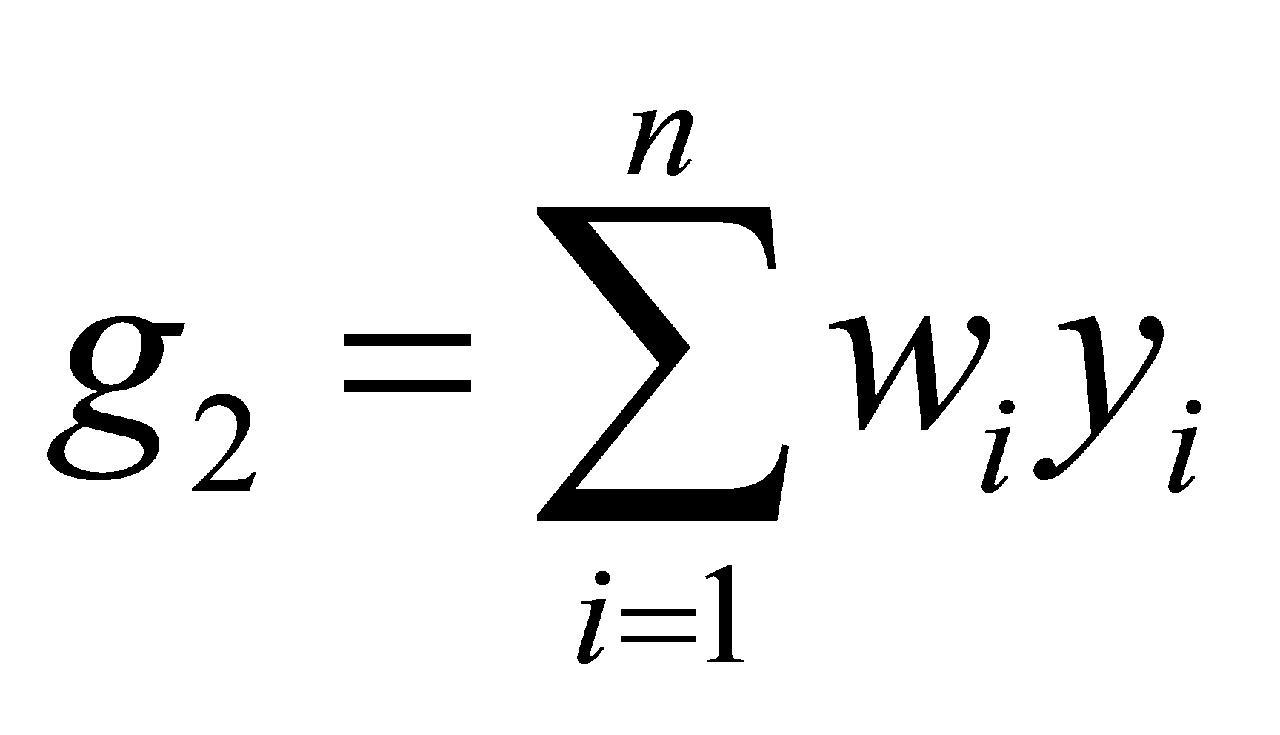 (2)
(2)
同一任务不同设备上检验的时间不同,智能排期时应尽可能地降低各设备的最优完成时间,提高设备使用率。最优完成时间为完成所有接受任务的前提下,最后一个设备转变为空闲状态的时间[3-4],计算方式见公式(3):
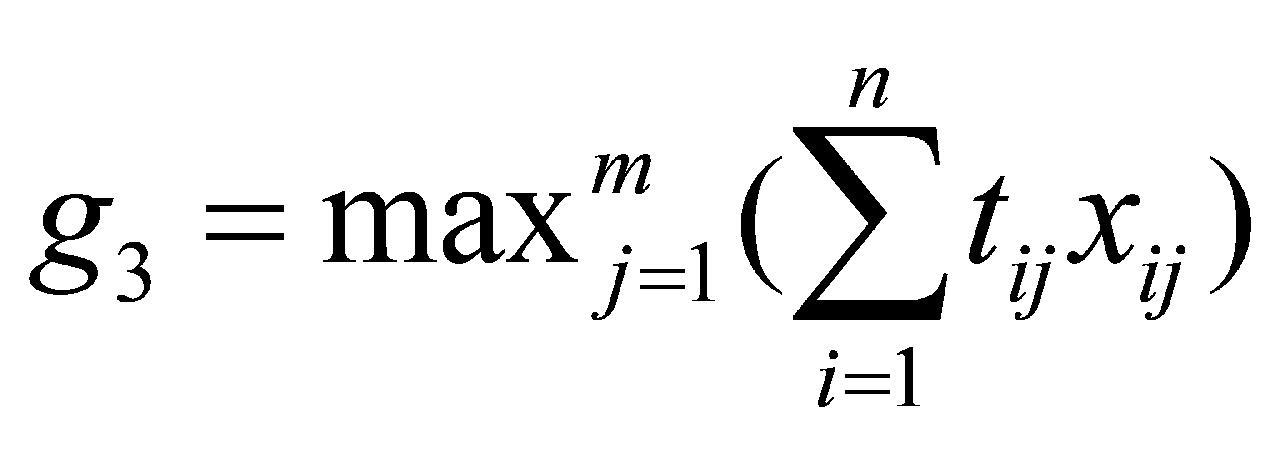 (3)
(3)
在保证接受的任务都能准时提交结果的前提下,智能排期时应尽可能地降低检验成本。任务检验的成本主要取决于所使用仪器设备的购买成本和使用次数,计算方式见公式(4):
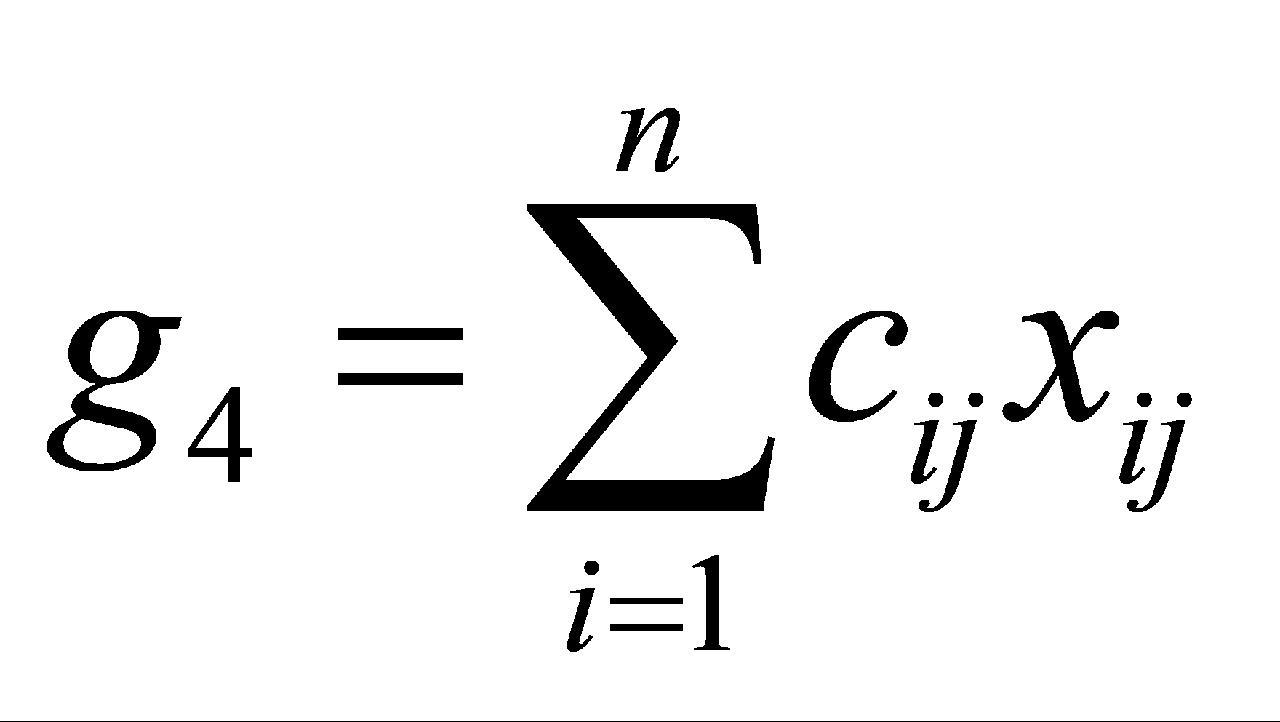 (4)
(4)
为使多目标优化智能排期模型可以有效求解,需设置一定的约束条件。
确保每个任务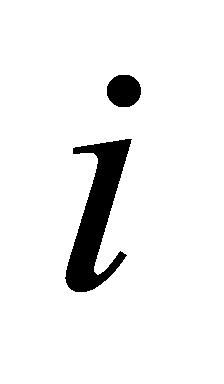 能在规定的结果提交日期
能在规定的结果提交日期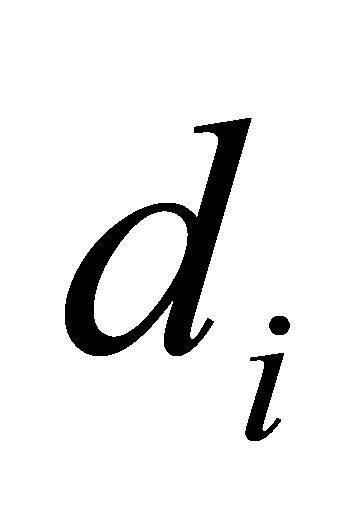 前完成,计算方式见公式(5):
前完成,计算方式见公式(5):
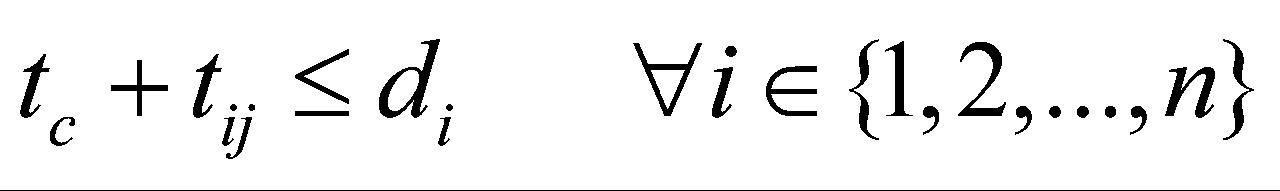 (5)
(5)
确保每项任务只能由1台设备处理[5-6],计算方式见公式(6):
 (6)
(6)
确保每个任务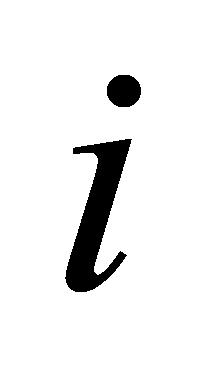 的只能分配给可用的设备j,计算方式见公式(7):
的只能分配给可用的设备j,计算方式见公式(7):
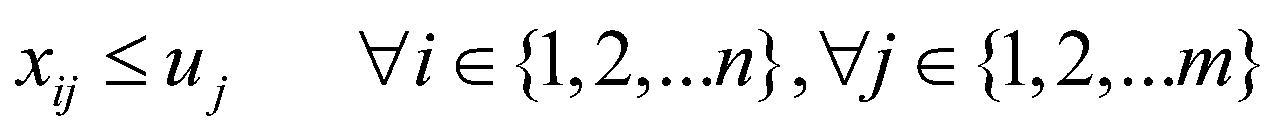 (7)
(7)
1.3 基于任务分类多目标优化模型
在智能排期模型中,任务的多样化和复杂化是不可避免的趋势。为了更好地应对现实世界中的各种任务需求,需要在任务调度模型中加入不同类型的任务[7],可依据优先级将任务分为紧急任务和普通任务。其中,紧急任务[8]具有较高的优先级,需要在短时间内完成,如果不及时处理可能会导致严重的后果;普通任务具有相对较低的优先级,可以在结果要求日期内逐步推进。
在明确了任务的优先级后,根据任务的不同性质进一步细分为周期任务、复合任务、绑定任务和单项任务,每种类型的任务都有其特定的管理要求。具体而言:(1)周期任务需要在固定的时间间隔内重复执行,要求系统在每个周期内都能按时完成,如机器的自检等。(2)复合任务由多个相关联的子任务组成,每个子任务需要按特定的顺序执行。复合任务的管理需要关注子任务之间的协调和衔接,确保整个任务能够顺利推进并按时完成。(3)绑定任务是指具有特定设备约束的任务,要求子任务必须在同一设备上连续执行。这些任务的特点在于子任务之间存在紧密的依赖关系,不能在不同的设备之间切换执行。(4)单项任务具有独立性,完成后即不再重复,与其他任务没有关联。
此外,为增强任务调度的稳健性,引入了时间冗余因子 。此因子用于增加每个任务的预计完成时间,以预防因不可预测因素导致的任务延期。此时,每个任务的实际执行时间将是其初始估计时间
。此因子用于增加每个任务的预计完成时间,以预防因不可预测因素导致的任务延期。此时,每个任务的实际执行时间将是其初始估计时间 的
的 倍。
倍。 可以通过人为规定,也可以通过历史数据进行计算。
可以通过人为规定,也可以通过历史数据进行计算。
为了使模型更加清晰和严谨,可以引入一些符号来表示各个变量和状态。加入任务分类后智能排期模型的参数设置见表2。
表2 基于任务分类的多目标优化模型的参数设置
Table 2 Parameter setting for multi-objective optimization model based on task classification
符号名称 | 符号描述 |
| 周期任务 |
| 第 |
| 第 |
| 所有任务的集合 |
| 任务 |
| 任务 |
| 任务 |
1.3.1 基于任务分类单设备任务排期
在原有的任务模型基础上,加入任务分类后,需要对决策逻辑进行相应的调整和扩展,具体步骤如下:
第一步,需要对任务序列进行排序。对于某一时刻输入的n个任务,存在不同优先级的,优先级高的先进行检验;同一优先级的,任务编号小的先进行检验。
第二步,需要对任务的性质进行判断。对于单项任务,直接判断能否在结果要求日期内完成,若能完成,则接受该任务,否则拒绝该任务。对于周期任务,先判断任务是否在当前周期内,如果任务在当前周期内,进一步判断是否能在结果要求日期内完成,若能完成,则接受该任务。对于复合任务和绑定任务,需要判断其子任务是否都能在结果要求日期内完成,若存在一个子任务无法在结果要求日期内完成,则拒绝该任务。
第三步,需要判断任务列表是否为空。若任务序列不为空,则返回第二步;若任务序列为空,则任务排期结束。
基于任务分类单设备任务排期流程如图3所示。
1.3.2 基于任务分类多设备任务排期
加入任务分类后,多目标优化模型的目标函数保持不变,但为满足不同任务类型的要求,需要根据不同的性质增加相应的约束条件。
(1)紧急任务:确保在同一设备情况下,紧急任务的开始时间不晚于其他任务的开始时间。在仪器设备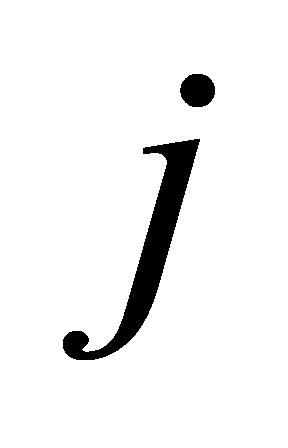 上进行检验时,紧急任务
上进行检验时,紧急任务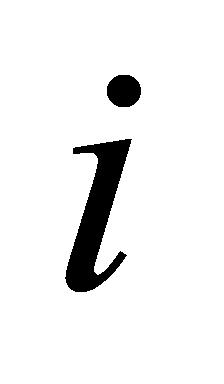 的开始时间不晚于非紧急任务
的开始时间不晚于非紧急任务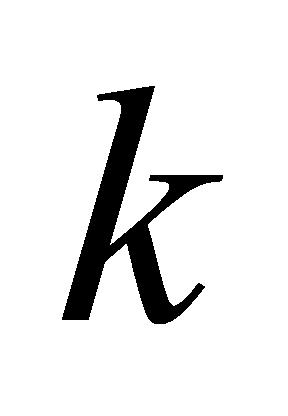 的开始时间,如公式(8)所示:
的开始时间,如公式(8)所示:
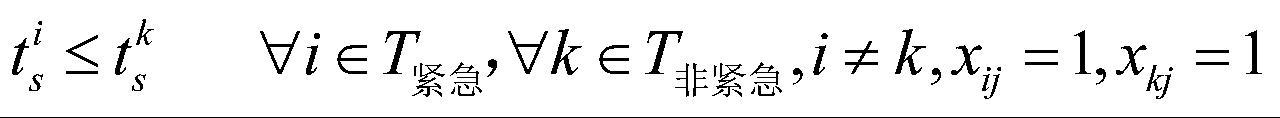 (8)
(8)
(2)周期任务:确保周期任务在每个周期内完成。对于周期任务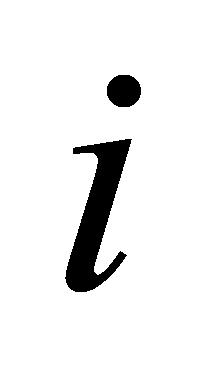 ,其在仪器设备
,其在仪器设备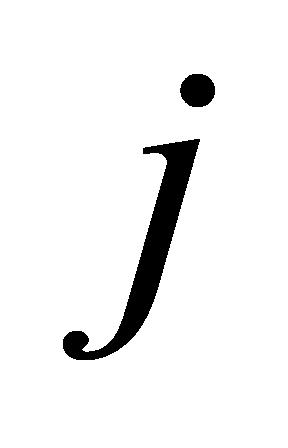 上的完成时间不能大于周期任务
上的完成时间不能大于周期任务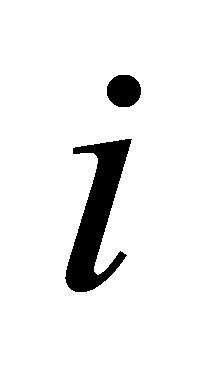 的周期,如公式(9)所示:
的周期,如公式(9)所示:
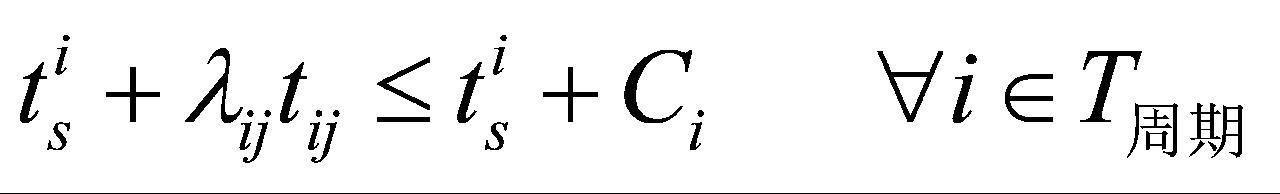 (9)
(9)
(3)复合任务:确保复合任务中的子任务按照特定顺序执行。对于复合任务中不相同的两个子任务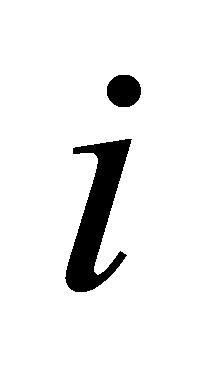 和
和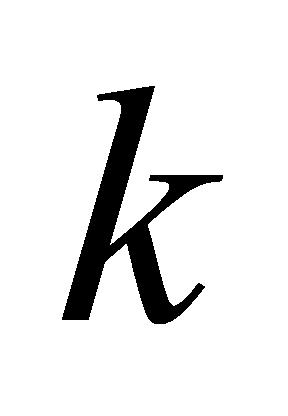 ,子任务i的结束时间不大于子任务k的开始时间,如公式(10)所示:
,子任务i的结束时间不大于子任务k的开始时间,如公式(10)所示:
 (10)
(10)
(4)绑定任务:确保绑定任务中的子任务在同一设备上进行。对于绑定任务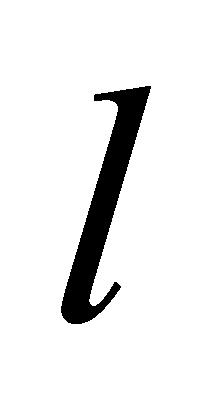 中不相同的两个子任务
中不相同的两个子任务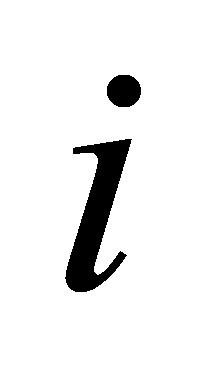 和
和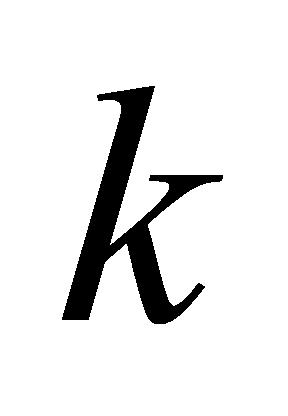 ,若子任务
,若子任务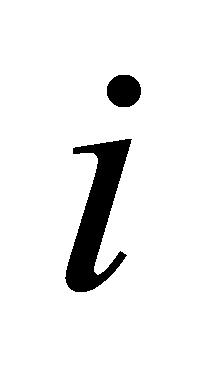 在仪器设备
在仪器设备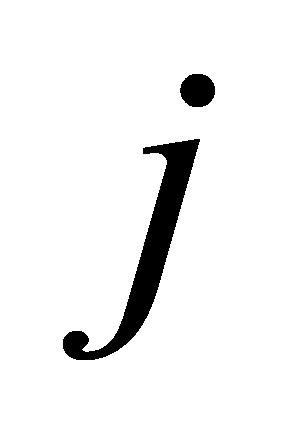 上进行检验,则
上进行检验,则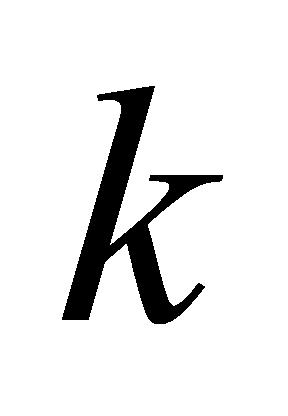 要在仪器设备
要在仪器设备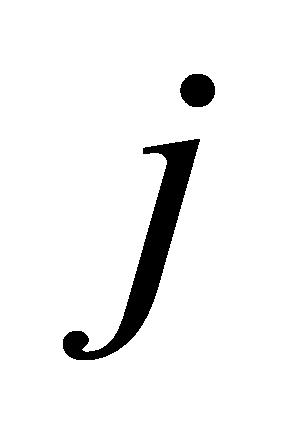 上进行检验,如公式(11)所示:
上进行检验,如公式(11)所示:
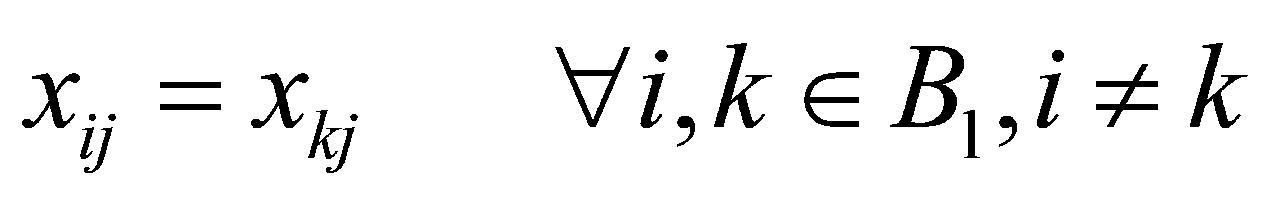 (11)
(11)
2 NSGA-Ⅱ算法设计
智能排期问题具有多目标、多约束、非线性等特点,普通的算法很难取得较好的求解效果。为有效解决这一多目标优化问题,本研究采用带精英策略的NSGA-Ⅱ[9-13]算法进行求解。该算法可以提高算法的运行速度和鲁棒性,保证非劣最优解的均匀分布,增强寻优速度和寻优能力。NSGA-Ⅱ算法流程图如图4所示。
第一步,输入信息和初始化参数。输入需要排期的任务信息和设备信息,同时,初始化NSGA-Ⅱ算法中的参数,包括种群大小、最大迭代次数、交叉概率和变异概率。
第二步,初始化种群。由于排期时要确定每个任务对应的仪器设备,因此,染色体采用整数编码,即每个染色体的元素对应着某个任务应分配给哪台设备。这一初始种群是算法优化过程的基础,为后续的选择、交叉和变异操作提供了初始材料。
第三步,计算适应度值。为更好地评估和选择最优解,进而更好地指导选择、交叉和变异等操作,本研究建立综合评价模型作为适值函数,以评估不同解的优劣。
图4 NSGA-Ⅱ算法流程图
Fig.4 NSGA-Ⅱ Algorithm flowchart
第四步,对初始种群进行非支配排序,并对每个非支配层中的方案计算拥挤度距离。非支配排序能识别出在多个目标上表现优异的解,而拥挤度距离则用于评估这些解之间的分布密度,确保种群多样性。根据非支配关系及个体的拥挤度选取合适的个体组成新的父代,从而保证下一代能够在优化空间中更广泛地探索。
第五步,通过交叉和变异操作,从父代中产生新的子代。这个过程不断重复,直到达到预设的最大迭代次数。当达到预设的最大迭代次数后,从最终种群中提取Pareto最优解集。Pareto最优解集是指在多目标优化问题中,不存在其他任何解可以在不使至少一个目标变差的情况下使得至少一个目标变得更好,即:这些解代表了不同目标之间的最佳折中方案,在多个目标之间达到最佳平衡。
最后,判断种群代数是否达到预先设定的最大迭代次数,不满足则将种群迭代次数加1并转向步骤四,满足条件则从中挑选出分数最高的解作为本次优化的最优解。
3 综合评价模型
通过NSGA-Ⅱ计算可得到Pareto解集,建立综合评价模型用于评估和选择最优解。不同的综合评价模型会产生不同的最优解,从而影响排期的结果。本研究将探讨两种主要综合评价模型——极值归一化评价模型和加权TOPSIS评价模型,并分析它们各自的优缺点,以期为智能排期模型提供科学合理的评价机制。
3.1 极值归一化评价模型
极值归一化评价模型是一种常用的多属性决策方法,它通过将各个属性值转化为无量纲的形式来消除不同属性间量纲的影响,进而实现对不同方案的综合评价。其主要优点在于计算过程简单明了,易于理解和操作,能够有效地处理属性间存在显著差异的情况。此外,该方法对于数据的要求相对较低,适用于初步筛选或粗略比较的情形。
首先,需要综合评价指标和不同方案的数量,构造二维评价矩阵 ,然后根据矩阵计算制定方案的指标评价值,具体步骤如下:
,然后根据矩阵计算制定方案的指标评价值,具体步骤如下:
(1)规范化决策矩阵。在本研究中,任务完成率g1、任务收益g2为正向指标,设备最优完成时间 和任务检验成本
和任务检验成本 为负向指标。对于正向指标,
为负向指标。对于正向指标, 。对于负向指标,
。对于负向指标, 。其中,
。其中,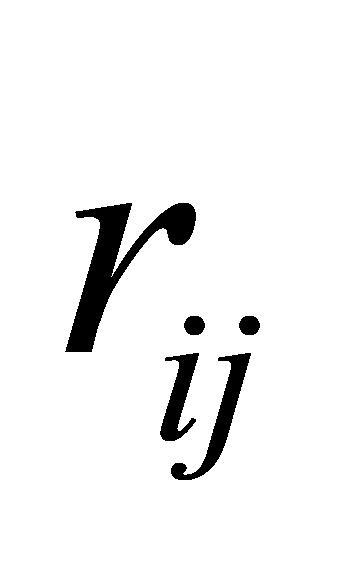 是归一化后的值,
是归一化后的值,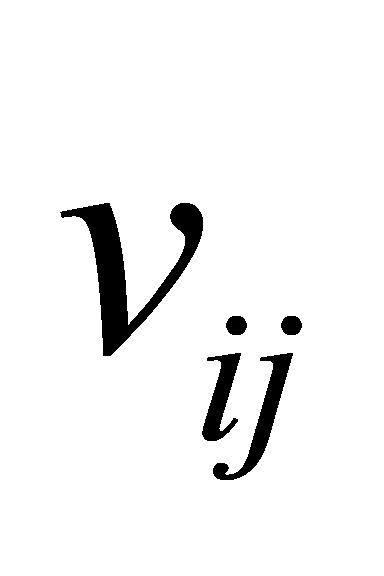 是原始值,
是原始值, 是对应指标的最大值,
是对应指标的最大值, 是对应指标的最小值。
是对应指标的最小值。
(2)计算加权归一化值: 。其中,
。其中,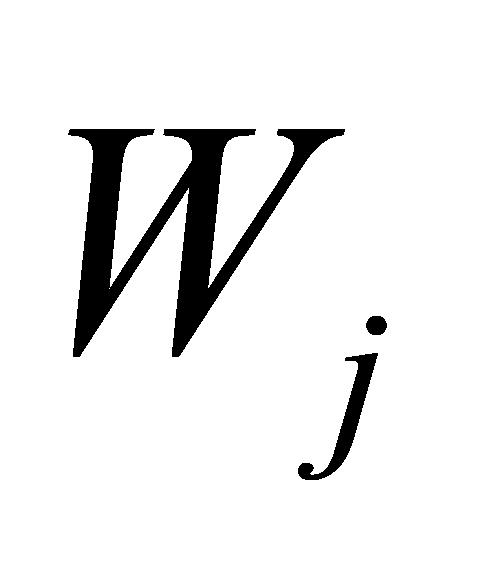 是指标j的权重,
是指标j的权重,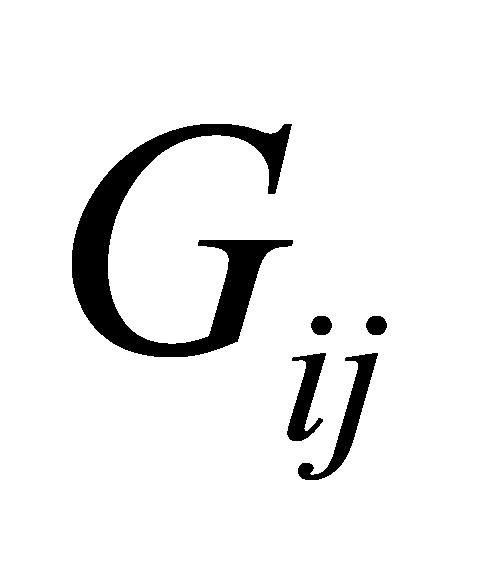 是加权归一化值。本研究设置4个指标的权重分别为0.5、0.3、0.1和0.1。
是加权归一化值。本研究设置4个指标的权重分别为0.5、0.3、0.1和0.1。
(3)计算综合评价值。将每个方案在所有指标下的加权归一化值相加,得到每个方案的综合评分。
(4)排序。根据方案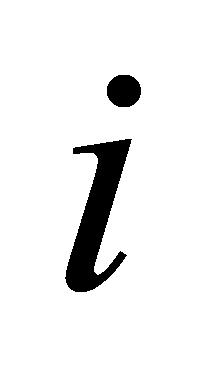 的综合评价值
的综合评价值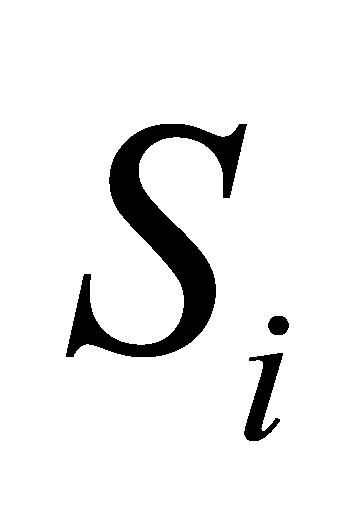 对方案进行排序,值越大表示方案越好。
对方案进行排序,值越大表示方案越好。
3.2 加权TOPSIS评价模型
加权TOPSIS评价模型则提供了一种更为精细和科学的决策支持工具。该模型通过构造多目标决策矩阵,采用逼近理想解的排序方法,按照每个指标与理想化目标的接近程度进行排序,从而计算每个评价事物与理想最优解和最劣解的综合距离[14-16]。加权优劣解距离法(Technique for Order Preference by Similarity to an Ideal Solution,TOPSIS)的优点在于不仅考虑了每个属性的重要性,还充分体现了备选方案与理想状态之间的相对接近程度,使得评价结果更加合理和准确。但是,这种方法也面临一些挑战,比如权重分配的主观性强,需要决策者具备较高的专业知识和经验;同时,计算复杂度较高,对于大规模数据处理可能存在效率问题。
首先,需要综合评价指标和不同方案的数量,构造二维评价矩阵 ,然后根据矩阵计算制定方案的指标评价值,具体步骤如下:
,然后根据矩阵计算制定方案的指标评价值,具体步骤如下:
(1)规范化决策矩阵。在本研究中,任务完成率g1,任务收益g2为正向指标,设备最优完成时间 和任务检验成本
和任务检验成本 为负向指标。对于正向指标,
为负向指标。对于正向指标,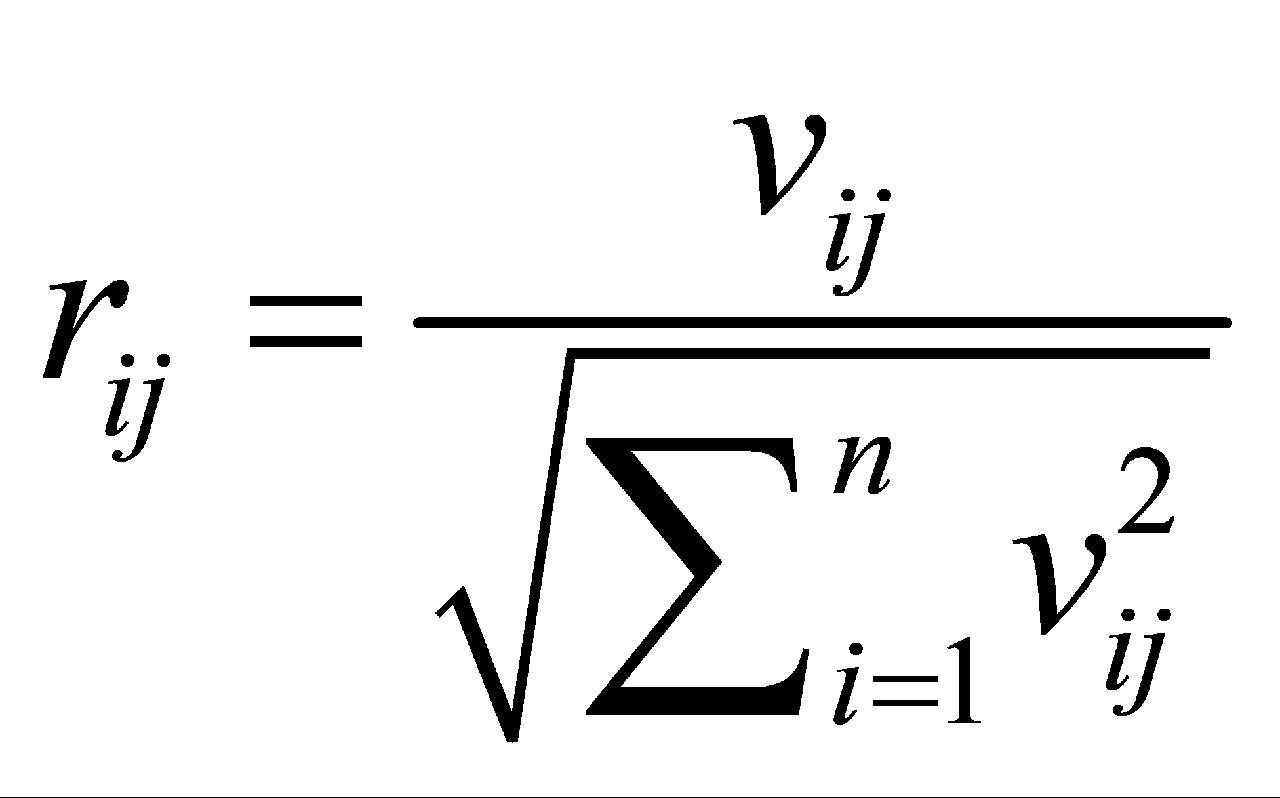 。对于负向指标,
。对于负向指标,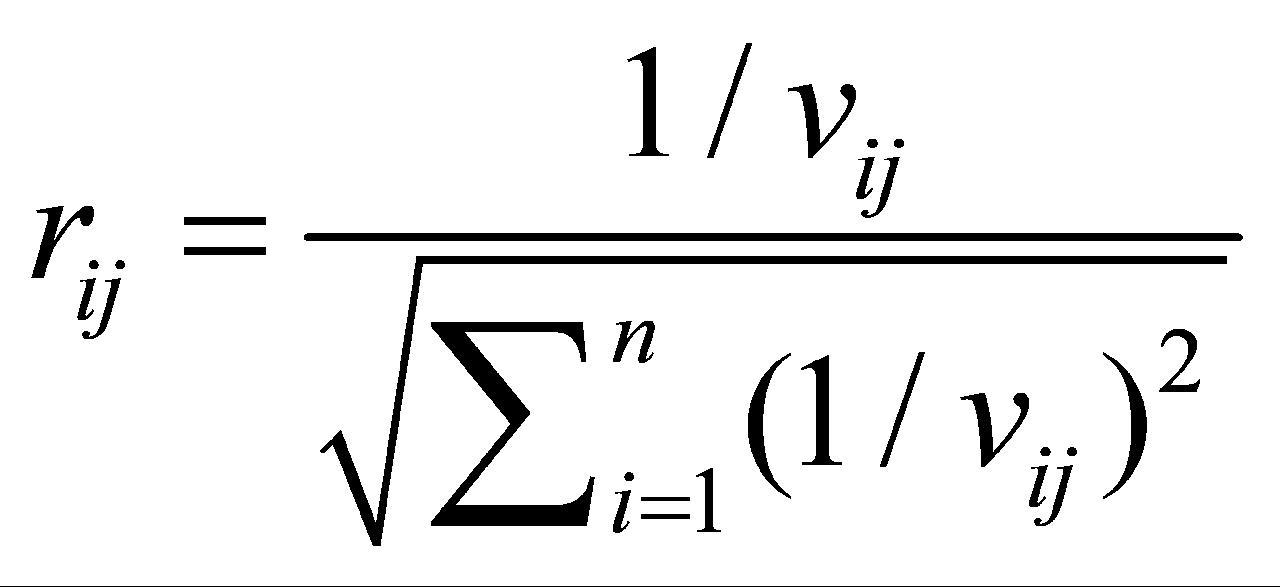 。
。
(2)构建加权规范化决策矩阵: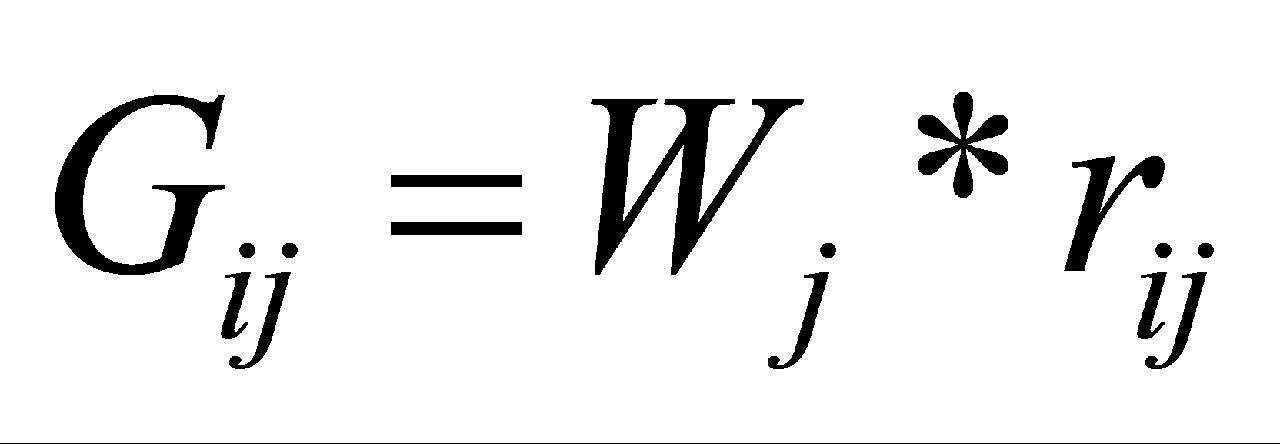 。其中,
。其中,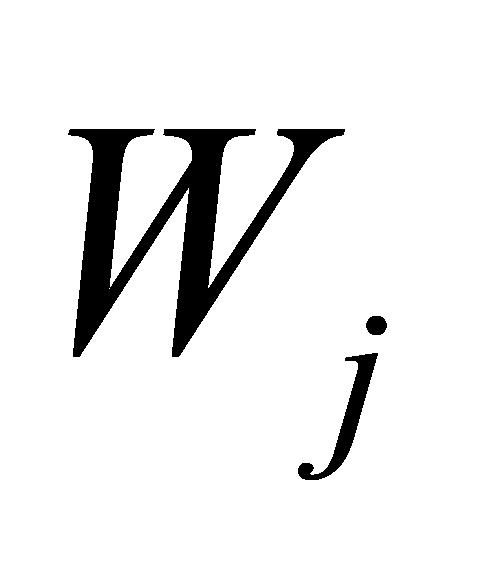 是指标j的权重,
是指标j的权重,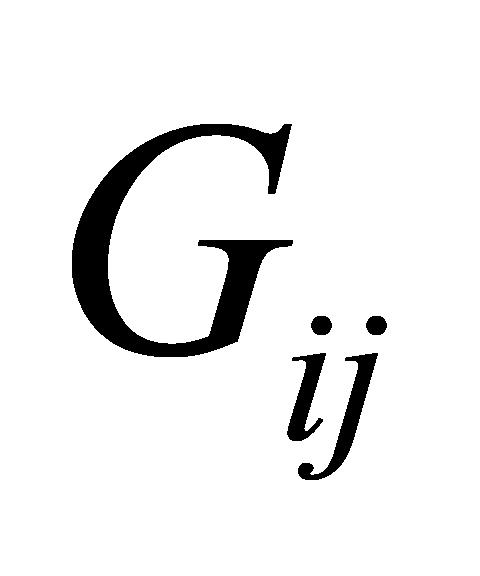 是加权归一化值。本研究设置4个指标的权重分别为0.5、0.3、0.1和0.1。
是加权归一化值。本研究设置4个指标的权重分别为0.5、0.3、0.1和0.1。
(3)计算评价数据到理想解和负理想解的距离。本研究采用欧氏距离来衡量不同解之间的距离。
(4)计算贴近值。根据评价指标与理想解和负理想解的欧氏距离,计算得到评价指标与理想解的贴近值,并将贴近值进行排序,得到各评价指标的评价结果[17]: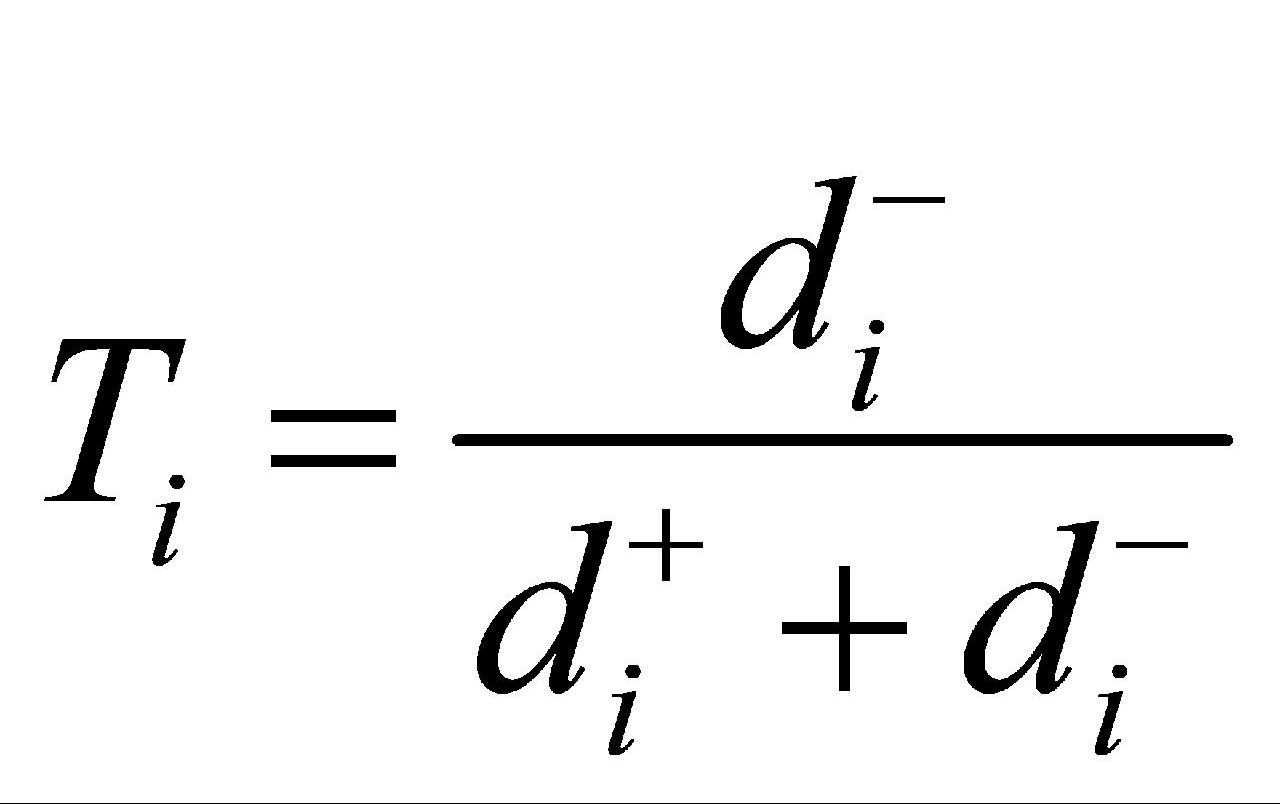 。其中,
。其中,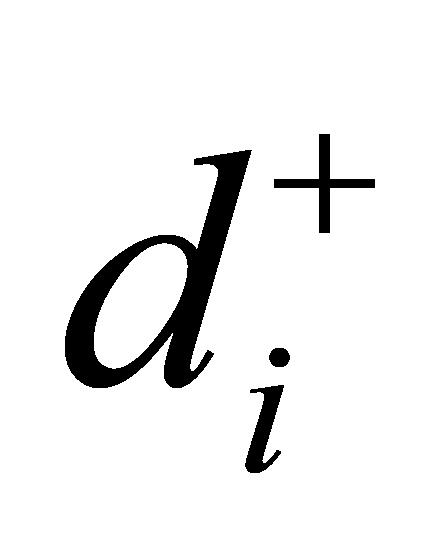 为与理想解的欧氏距离;
为与理想解的欧氏距离;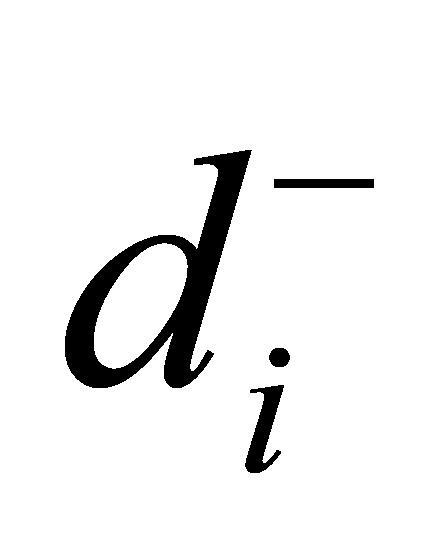 为与负理想解的欧氏距离;
为与负理想解的欧氏距离;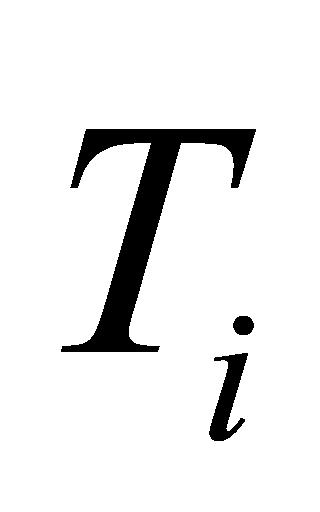 为第
为第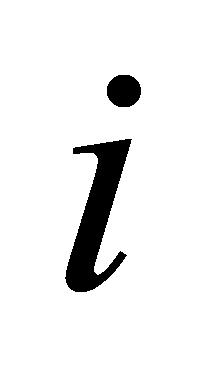 个评价指标与理想解的贴近值。
个评价指标与理想解的贴近值。
(5)排序。相对接近值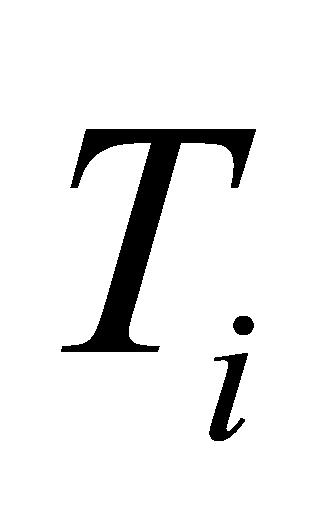 的值越大表示方案越好。
的值越大表示方案越好。
4 仿真实验
选取20个任务、5台设备进行仿真实验,任务信息、仪器设备信息见表3、表4。
表3 仿真实验的任务信息
Table 3 Task information
编号 | 收益 | 日期 | 任务类型1 | 任务类型2 | 其他 |
1 | 10 | 100 | 普通任务 | 单项任务 | |
2 | 16 | 108 | 普通任务 | 复合任务 | 任务2、3、4为复合任务1的三个子任务 |
3 | 13 | 106 | 普通任务 | 复合任务 | |
4 | 14 | 78 | 普通任务 | 复合任务 | |
5 | 11 | 38 | 紧急任务 | 普通任务 | |
6 | 11 | 83 | 普通任务 | 普通任务 | |
7 | 8 | 83 | 普通任务 | 普通任务 | |
8 | 19 | 79 | 普通任务 | 绑定任务 | 任务8、9为绑定任务1的两个子任务 |
9 | 13 | 102 | 普通任务 | 绑定任务 | |
10 | 13 | 90 | 普通任务 | 周期任务 | 周期为108 |
11 | 17 | 104 | 普通任务 | 单项任务 | |
12 | 14 | 87 | 普通任务 | 单项任务 | |
13 | 19 | 102 | 普通任务 | 单项任务 | |
14 | 7 | 88 | 普通任务 | 单项任务 | |
15 | 14 | 105 | 普通任务 | 单项任务 | |
16 | 9 | 105 | 普通任务 | 单项任务 | |
17 | 11 | 107 | 普通任务 | 单项任务 | |
18 | 14 | 93 | 普通任务 | 单项任务 | |
19 | 7 | 73 | 紧急任务 | 复合任务 | 任务19、20为复合任务2的两个子任务 |
20 | 19 | 75 | 紧急任务 | 复合任务 |
注: 任务类型1表示该任务按照优先级分类所属类型; 任务类型2表示该任务按照性质分类所属类型; 其他表示不同类型任务的一些特性性质.
在没有算法指导的情况下,通常会采取一种直接的方法来进行任务分配,即每当一台设备变得空闲时,就会立即着手处理任务序列中的首个任务。这种做法虽然简单易行,但在面对资源有限的情况时难以兼顾效率和公平。人工排期甘特图如图5所示。
人工排期时,20个任务全部都能在结果提交日前准时检验,故任务接受率为100%;计算完成20个任务的收益为259个收益单位,最优完成时间为68 h,成本为60个成本单位。
采用本研究提出的NSGA-Ⅱ算法对测试数据进行求解时,算法主要参数见表5。
表5 NSGA-Ⅱ算法的主要参数
Table 5 Main parameters
参数 | 值 |
种群大小 | 100 |
最大迭代次数 | 500 |
交叉概率Pc | 0.9 |
变异概率Pm | 0.2 |
基于以上数据得到Pareto最优解集和智能排期甘特图如图6、图7所示。
图6 Pareto最优解集
Fig.6 Pareto optimal solution set
智能排期时,20个任务全部都能在结果提交日前完成检验,故任务接受率为100%;计算完成20个任务的收益为259个收益单位,最优完成时间为46 h,成本为59个成本单位。
经过实验分析,本研究所提出的多目标优化模型展现出了显著优势。在任务接受率和任务收益相等的情况下,智能排期模型在最优完成时间和任务成本上均得到了改进。最优完成时间从68 h减少至42 h,缩短了38.23%;任务成本从60个单位降低到59个单位,降低了1.67%,这些结果充分证明了该算法的高效性。
5 动态调度机制
在实际情况中,无论是遇到新检验任务还是完成已有任务,都会导致任务量n随着时间的推移而不断变化。为更好地应对实际情况中任务量n并非固定数值的情况,本研究进一步建立动态调度机制,将时间划分为一系列离散的时间点,每个时间点对应着一次任务的输入。在每个时间点上,智能排期模型都会根据当前的任务情况对任务序列进行重新排序并决定是否接受新任务。
在任意时间点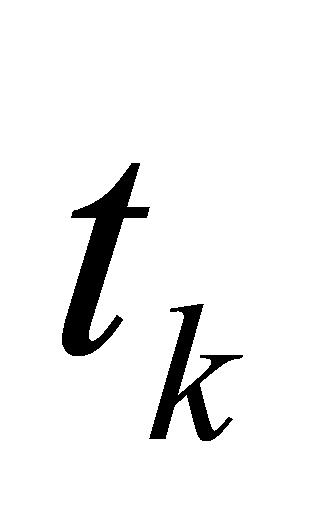 ,首先应用 NSGA-Ⅱ算法对当前待处理的
,首先应用 NSGA-Ⅱ算法对当前待处理的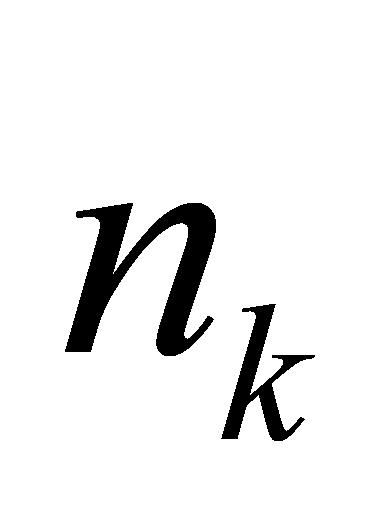 个任务进行调度,以寻求一个高质量的排期方案。随时间推移至下一个时间点
个任务进行调度,以寻求一个高质量的排期方案。随时间推移至下一个时间点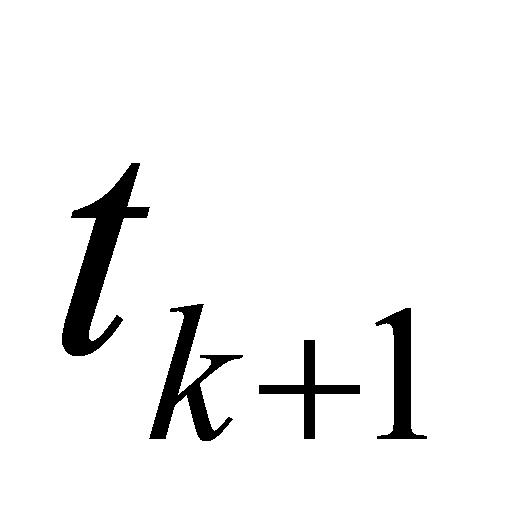 ,则需要根据时间点
,则需要根据时间点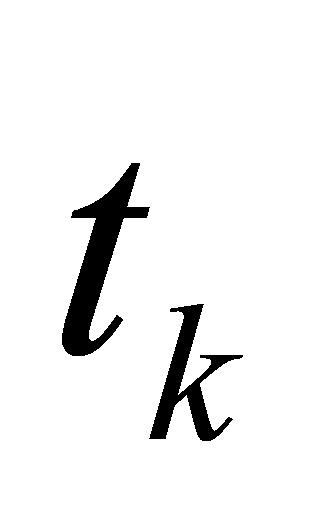 的任务完成情况采取不同的排期策略。此时,若时间点
的任务完成情况采取不同的排期策略。此时,若时间点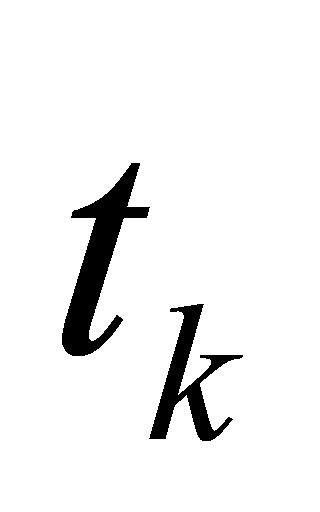 输入的
输入的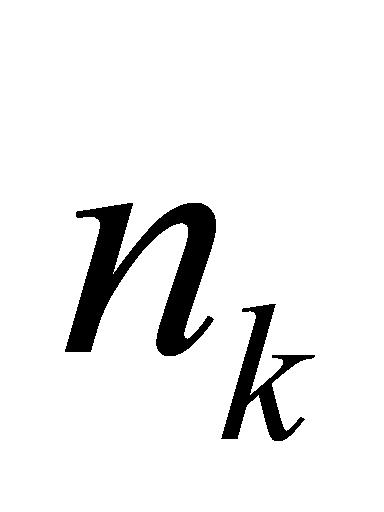 个任务均已完成,则直接针对
个任务均已完成,则直接针对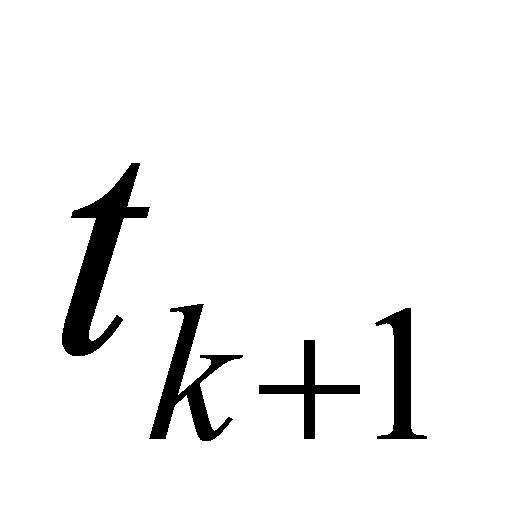 时间点新出现的
时间点新出现的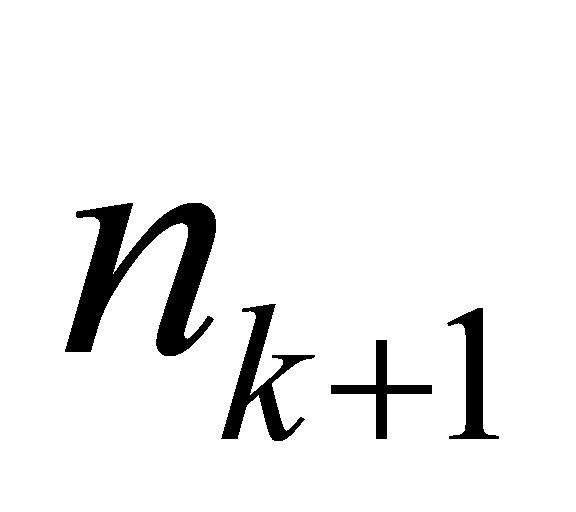 个任务制定调度方案;若
个任务制定调度方案;若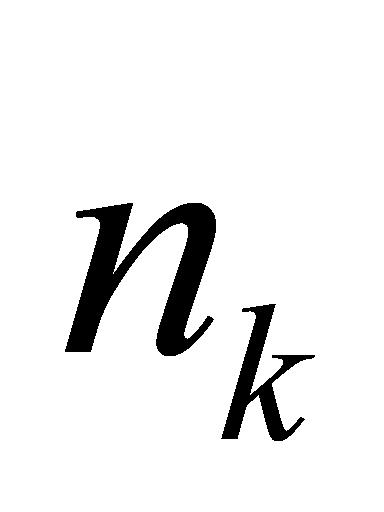 个任务中存在尚未开始检验的任务,则将这些任务与新抵达的
个任务中存在尚未开始检验的任务,则将这些任务与新抵达的 个任务共同考虑,再次借助 NSGA-Ⅱ 算法探寻最优的排期方案。该机制在未来各时间点上持续实行,直至全部已排期任务检验完成。
个任务共同考虑,再次借助 NSGA-Ⅱ 算法探寻最优的排期方案。该机制在未来各时间点上持续实行,直至全部已排期任务检验完成。
在整个过程中,需严格遵循以下准则:凡是已被接受的任务,一律不得拒绝,其必须融入新的排期计划之内。这意味着每个时间点上的排期方案都是在之前基础上进行的增量调整,而非完全重置。
建立动态调度机制不仅使智能排期模型更加贴近实际情况下的动态变化,还能通过对已排期任务进行再分配来提高仪器设备利用率,为复杂的现实环境提供了更为灵活、可靠的解决方案。
6 结语
本研究针对实验室资源约束条件下仪器设备的高效调度问题,提出了一个智能排期模型,该模型通过构建多目标规划调度模型并采用NSGA-Ⅱ算法求解。仿真实验表明,使用该模型后能显著缩短最优完成时间和降低任务成本。加入任务分类和动态机制后,该模型能够实现执行过程中的任务再分配,与实际情况更为符合。与人工排期相比,智能排期模型在任务完成率和资源利用率上均得到改进。这些成果验证了智能排期模型的有效性,为其实现从理论到实践的转化提供了坚实的基础。
尽管智能排期模型在仪器设备管理上展现了诸多优势,但也存在一些局限性。当前模型对数据输入有较高的要求,数据的准确性和完整性对排期结果有较大的影响。为应对这一不足,后期研究可以考虑将智能排期模型与模糊逻辑算法相结合,利用模糊逻辑算法能够处理不确定性和不完全信息的特点,降低模型对数据的依赖,增强模型的鲁棒性和容错能力,提高整体的调度效果。未来,随着智能排期模型的不断改进和完善,它将不仅限于简单的日程安排工具,而是成为提升实验室整体效率的关键驱动力,为实现更加智能化的实验室管理和仪器设备调度提供强有力的支持。
参考文献
[1]李笑笑, 杨晓英, 张志伟, 等. 基于改进NSGA-Ⅱ的轴承企业生产智能排程[J]. 轴承, 2024(10): 65-75.
[2]宋昌兴, 阮景奎, 王宸. 基于混合多目标遗传算法的柔性作业车间调度问题研究[J]. 机电工程, 2021, 38(2): 169-176.
[3] Wang Jianhua, Wu Chuanyu, Peng Yongtao. Multi-objective scheduling for an energy-efficient flexible job shop problem with peak power constraint[J]. Applied Soft Computing, 2024, 167(Part A): 112330.
[4]杨欣, 杨晓英, 闫欢欢, 等. 基于混合鲸鱼算法的风电玻板生产智能排程[J]. 船舶工程, 2024, 46(5): 120-128+159.
[5]彭相涵, 朱玉杰. 基于订单优先级和改进粒子群算法的生产排程优化[J]. 轻工机械, 2024, 42(5): 97-104.
[6] Dauod, Husam Li, Debiao Yoon, et al. Multi-objective optimization of the order scheduling problem in mail-order pharmacy automation systems[J]. International Journal of Advanced Manufacturing Technology, 2018, 99(1-4): 73-83.
[7] Chen Zeyun. Port Logistics Function Evaluation Model Based on Entropy Weight TOPSIS Method[J]. Discrete Dynamics in Nature and Society, 2022(1): 5006900.
[8] Mousavi-Nasab, Seyed Hadi, Sotoudeh-Anvari, et al. A comprehensive MCDM-based approach using TOPSIS, COPRAS and DEA as an auxiliary tool for material selection problems[J]. Materials & Design, 2017, 121: 237-253.
[9]陈小庆, 侯中喜, 郭良民, 等. 基于NSGA-Ⅱ的改进多目标遗传算法[J]. 计算机应用, 2006(10): 2453-2456.
[10]王秀丽, 李淑慧, 陈皓勇, 等. 基于非支配遗传算法及协同进化算法的多目标多区域电网规划[J]. 中国电机工程学报, 2006(12): 11-15.
[11]王峰, 韩孟臣, 赵耀宇, 等. 基于改进NSGA-Ⅱ算法求解多目标资源受限项目调度问题[J]. 控制与决策, 2021, 36(3): 669-676.
[12]冯翔, 杨红雨. 进港飞机调度多目标优化问题的改进NSGA-Ⅱ算法[J]. 电子科技大学学报, 2014, 43(1): 66-70.
[13]张国富, 王永奇, 苏兆品, 等. 应急救援物资多目标分配与调度问题建模与求解[J]. 控制与决策, 2017, 32(1): 86-92.
[14] Yoon K Paul, Kim Won Kyung. The behavioral TOPSIS[J].Expert Systems with Applications, 2017, 89: 266-272.
[15] Ramin Nabizadeh, Samira Yousefzadeh, Kamyar Yaghmaeian, et al. Bottled water quality ranking via the multiple criteria decision making process: a case study of two stage fuzzy AHP and TOPSIS[J]. Environmental Science and Pollution Research, 2022, 29(14): 20437-20448.
[16]徐龙江, 王洋, 孙振海, 等. 基于人员承载力画像的多任务智能排期系统[J]. 农村电气化, 2022(1): 36-41.
[17]周秋艳, 肖满生, 张龙信, 等. 多约束条件下生产排程智能优化技术[J]. 计算机科学, 2021, 48(3): 239-245.
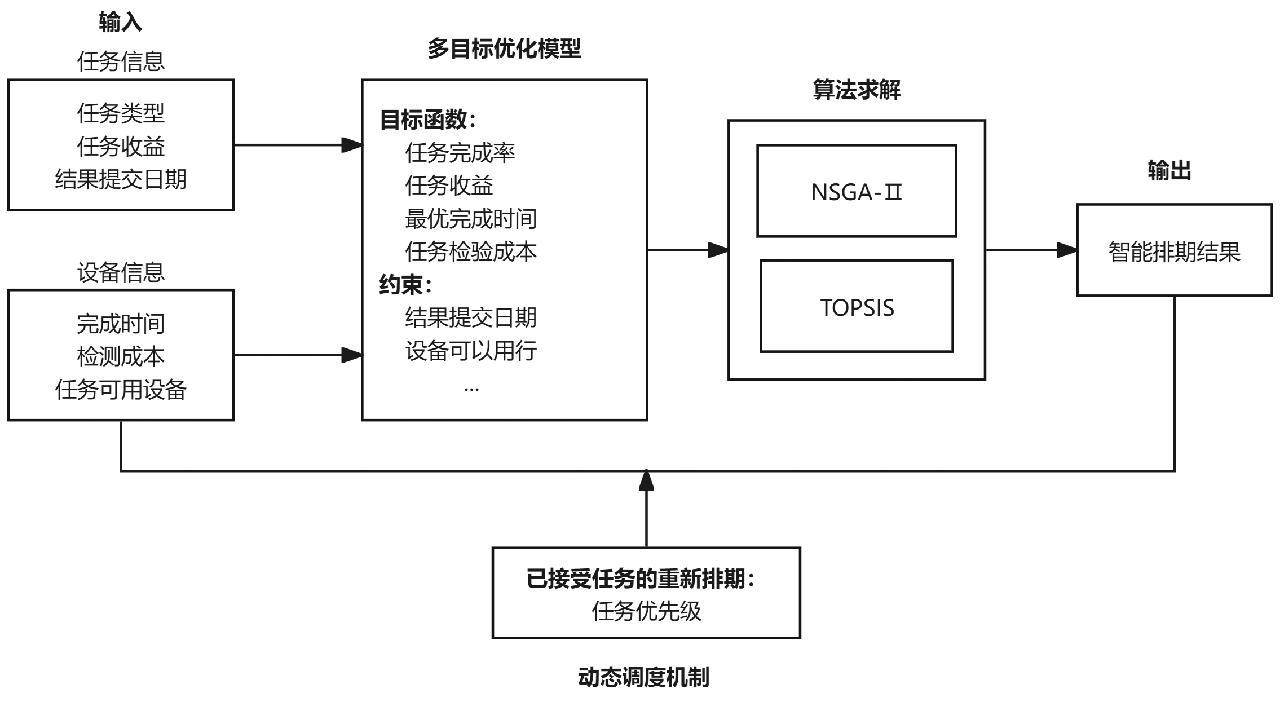
图1 智能排期模型
Fig.1 Model of intelligent scheduling
表1 多目标优化模型的参数设置
Table 1 Parameter setting of multi-objective optimization model
符号名称 | 符号描述 |
| 任务编号 : |
| 仪器设备编号 : |
| 仪器设备数量 |
| 任务 |
| 完成任务 |
| 任务 |
| 任务 |
| 否则设置为 1 |
| 否则设置为 0 |
| 变量设置为 1, 否则设置为 0 |
| 否则设置为 0 |
| 当前时刻 |
图3 基于任务分类单设备任务排期流程图
Fig.3 Flowchart for single-equipment task scheduling based on task classification

表4 仿真实验的设备信息
Table 4 Equipment information
任务编号 | 可用设备 | 检验时间 | 检验成本 | 任务编号 | 可用设备 | 检验时间 | 检验成本 |
1 | [1,0,0,0,1] | [16,0,0,0,17] | [3,0,0,0,5] | 11 | [1,1,1,1,1] | [5,1,22,22,17] | [2,3,5,4,2] |
2 | [1,1,1,1,1] | [3,12,12,5,2] | [4,5,3,4,1] | 12 | [0,1,0,0,0] | [0,10,0,0,0] | [0,5,0,0,0] |
3 | [1,1,1,1,0] | [4,9,15,3,0] | [5,4,5,4,0] | 13 | [1,1,0,0,0] | [3,19,0,0,0] | [5,5,0,0,0] |
4 | [1,1,0,1,1] | [10,20,0,21,17] | [4,4,0,3,5] | 14 | [1,1,1,1,1] | [23,1,19,13,8] | [2,3,3,4,3] |
5 | [0,1,1,0,0] | [0,15,14,0,0] | [0,3,1,0,0] | 15 | [1,0,1,0,0] | [3,0,20,0,0] | [2,0,1,0,0] |
6 | [0,1,0,0,0] | [0,17,0,0,0] | [0,1,0,0,0] | 16 | [1,1,1,1,1] | [23,24,10,8,11] | [4,3,1,4,1] |
7 | [0,0,0,1,1] | [0,0,0,17, 19] | [0,0,0,1,5] | 17 | [1,1,1,1,1] | [10,7,16,10,13] | [2,4,1,3,1] |
8 | [1,1,0,0,0] | [15,18,0,0,0] | [4,5,0,0,0] | 18 | [1,1,0,1,1] | [3,15,0,5,9] | [2,2,0,3,4] |
9 | [1,0,0,0,0] | [21,0,0,0,0] | [1,0,0,0,0] | 19 | [0,1,1,0,0] | [0,17,17,0,0] | [0,4,3,0,0] |
10 | [0,1,1,1,1] | [0,2,2,19,24] | [0,4,4,4,1] | 20 | [0,1,1,0,1] | [0,7,23,0,7] | [0,2,2,0,4] |
注: 可用设备数组中“1”表示对应设备可检验该任务; 检验时间数组中数字表示任务在不同设备上检验需要的时间单位; 检验成本数组中数字表示任务在不同设备上检验需要的成本单位.

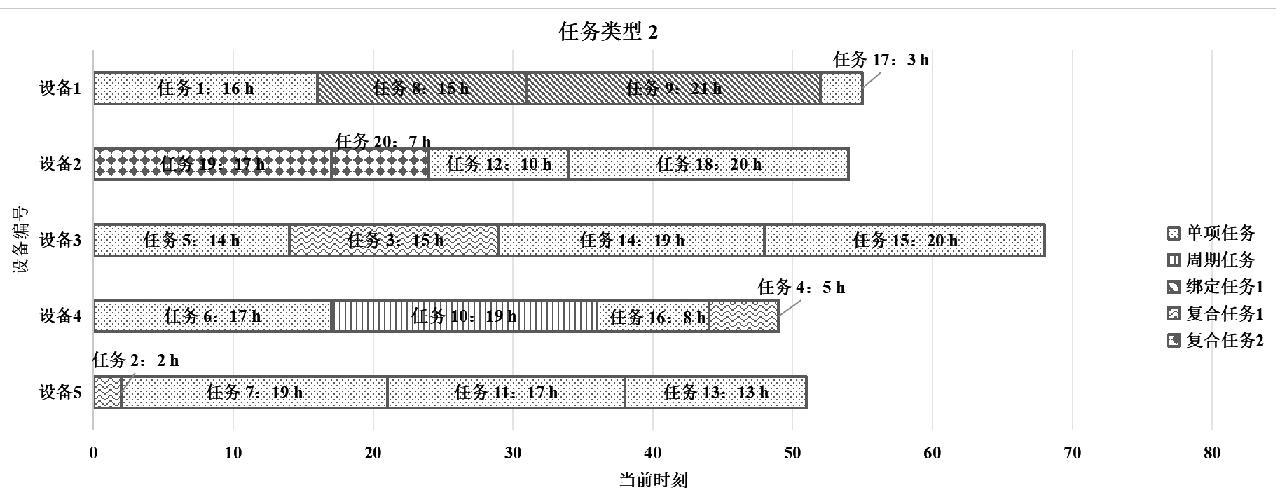
图5 人工排期甘特图
Fig.5 Gantt chart of manual scheduling

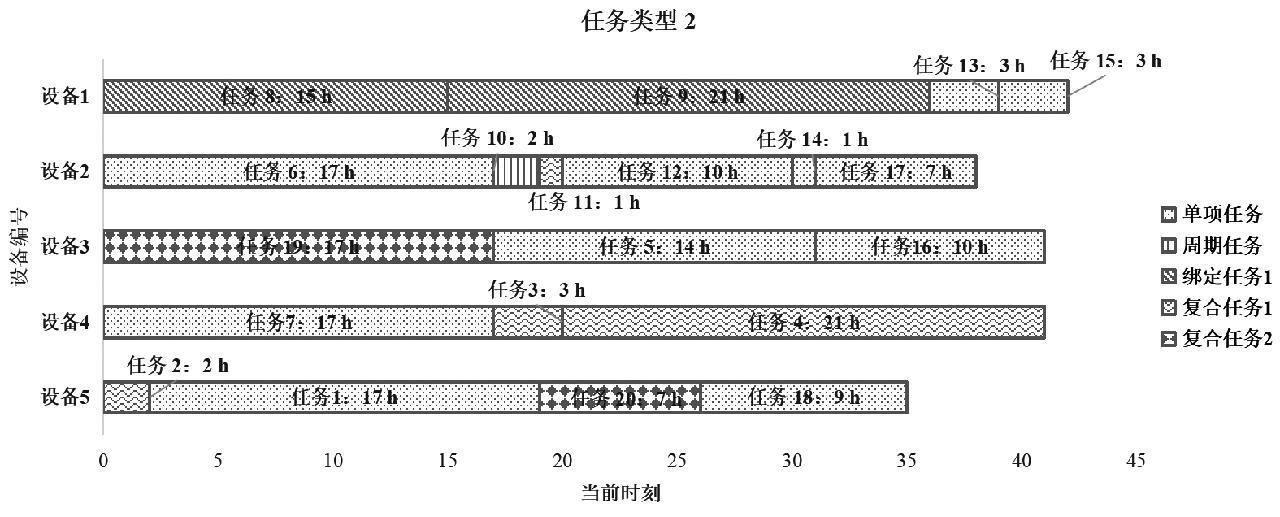
图7 智能排期甘特图
Fig.7 Gantt chart of intelligent scheduling